Nature and Characteristics of the Electric Field [Electrostatics (1958)]

16. The Nature and Definition of the Electric Field

Work in a physical sense is done on a body when a force is applied to it, causing it to move against a resistance in the direction of the force. When a boy pulls a sled, his hand is in contact with the rope and the rope is tied to the sled; when a carpenter swings a hammer, his hand must grasp the handle in intimate contact and the hammer does no work until its head comes in contact with the nail.

There are three distinct phenomena in which the rule of contact appears to be violated: gravitational attraction, magnetic attraction and repulsion, and electrostatic attraction and repulsion. All three follow the law of inverse squares, that is, that the force is inversely proportional to the square of the distance between the centers of the reacting bodies. But in all three reactions, contact between the body exerting the force and the body upon which the force acts is unnecessary.

Investigations of gravity, magnetism, and electrostatics have given rise to field theories for each of these phenomena. In the case of electrostatic forces, a condition of stress appears to exist in the medium surrounding an electric charge so that a force acts upon a positive or negative charge placed in this medium. This condition of stress is easily detectable when the charges are sufficiently large; when large enough, the medium itself may rupture causing an arc discharge, which is usually accompanied by a characteristic electric spark and heat. The ability of charged objects to influence each other over a distance is attributed to the stress in the medium, and the region in which this stress appears is known as the electric or electrostatic field.

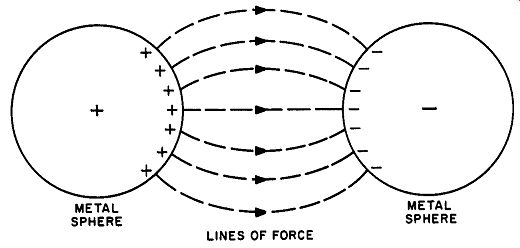
Fig. 9. An electrostatic field is considered to be made up of lines of force that pass from a positively charged body to a negatively charged one.

Electrostatic stress or distortion of the medium can be represented by lines of force. The direction of such a line of force is arbitrarily chosen as the path along which a unit positive charge would move if it were free to do so. A fairly complete "picture" of an electric field was first drawn up by Faraday who attributed the following characteristics to lines of force:

1. An electric field may be divided up into lines of force.

2. Each line terminates at a positive charge on one end and a negative charge on the other.

3. The lines, throughout the field, coincide with the direction of the electric stress.

4. The lines behave as though they were made of stretched elastic, always tending to contract and bring together the negative and positive charges.

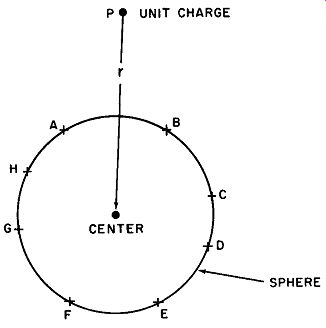
Fig. 10. Field conditions around a small charged sphere.

5. A line of force between two conducting surfaces must always meet the conducting surface perpendicularly. This must be so from the very nature of the assumed static conditions. If a line of force entered or left a conducting surface at any other angle than normal, it would have a tangential component at the surface which would cause the movement of charges within the conductor. This would constitute a continuous electric current and, since currents do not flow along the surface of the conductor in an electric field in a static system, the junction of the line of force and the surface must be a right angle. (See Fig. 9.) 17. The Equation of Field Intensity The intensity of an electric field is defined as the force acting on a unit charge, and is denoted by E. Thus, by definition:

F E= q (14)

in which (in the cgs system) F is in dynes, q is in esu, and E is in dynes per unit charge.

Equation 14 alone, however, is not sufficient for the solution of many problems. In addition, it is necessary to be able to find the number of lines of force associated with point charges. To determine the number of lines of force that leave or enter each unit charge, we first consider the field conditions in the vicinity of a small charged sphere (Fig. 10). The surface of the sphere contains q positive charges. At a distance r from the center of the sphere and lying well beyond the surface is a unit charge (one esu). The unit charge is close to positive charges A and B, at a greater distance from charges H, C, G and D, and at a still greater distance from F and E. Further more, from previous considerations (Section 4), we know that the charges are distributed uniformly around the surface of the sphere.

The question may then be asked, "What is the average effect of these distributed charges on the unit charge r cm away from the sphere's center?" By averaging the distances of the uniformly distributed charges, the tentative conclusion may be reached that the net effect of the surface charges is the same as though they were all concentrated at the center of the sphere. This conclusion may be further justified when it is recalled that lines of force must intersect a charged surface perpendicularly so that a continuation of each line must pass through the center of the sphere. (Any radius of a sphere intersects the surface of the sphere at right angles to it.) Thus, insofar as the effect of the surface charges upon a unit external charge is concerned, this charge is acted upon by a force that is identical to one that would be produced by q charges at the center of the sphere.

Coulomb's Law given in Equation 1 is written F = qq'/Kr2.

Many secondary equations derived from Coulomb's Law contain the factor 4pi. These equations are applied more frequently than the basic expression, and it is convenient to eliminate the 4pi from them.

This is accomplished by defining a new constant, eta_o, as follows:

… which yields

(16)

whence Coulomb's Law becomes

(17)

where q and q' are in coulombs, r is in meters, and F is in newtons.

From the numerical value of K given in Equation 11, we can state for the mks system that:

(18)

Example: Two alpha particles, each having a charge of 3.2 x 10^-19 coulombs, are separated by a distance of 10^-13 meters. Find the force of repulsion between them in dynes.

Solution: From Equation 17

S.2 X 10^-19 X S.2 X 10^-19 F=------------- 4 X S.14 X 8.85 X 10^-12 X (10-13) 2

= 9.17 x 10^-2 newtons

Because 1 newton = 10^5 dynes, F = 9170 dynes

Returning now to the charged sphere of Fig. 10 and its electric field, it has already been mentioned that the magnitude of the field is the force per unit charge (E = F /q). Force is a vector quantity, however, so that direction as well as magnitude must be assigned to the field. The direction of an electric field at a particular point in ...

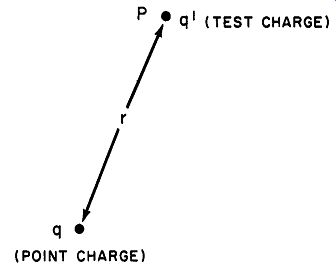
Fig, 11. The electric field of a point charge, q, acting on a test charge, q '.

... the field is arbitrarily taken as the direction of the force acting on a positive test charge placed at that point. Thus, the force on a negative charge such as an electron is considered opposite to the direction of the field.

The nature of the medium through which an electric field acts determines the value of the constant K in Coulomb's Law (K = 4 pi Eo), hence K is known as the dielectric constant of the medium. To determine electric field intensity at a point P separated from a point charge q by a distance r, consider a test charge having a charge magnitude equal to q' placed at P as in Fig. 11.

From Equation (17)

F= qq' 41ri

0r2

but electric field intensity (from Equation 14) is

F E= q' so that E= q 41ri

0r2 (19)

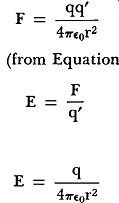
... and the direction of the field is away from the point charge q if it is positive and toward it if q is negative.

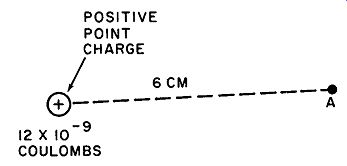
Fig. 12. Illustration for Ex ample.

Example: A point charge having a magnitude of plus 12 x 10^-9 coulombs is located 6 cm away from point A. Compute the electric field intensity at point A (Fig. 12) and state whether the field acts to the right or to the left.

Solution: The magnitude of the force vector acting on point A due to the positive charge is given by

12 X 10^-9 E =-------------- 4 X 3.14 X 8.85 X 10^-12 X (0.06) 2

E = 3.0 x 10^4 newtons per coulomb

Because the point charge is positive, the field is directed away from it or toward the right.

We are now prepared to discuss the method used to represent an electric field by lines of force. Any number of lines might be chosen to describe a field of given intensity, but if this were done, the resulting picture would be entirely qualitative with respect to field magnitude. In order to have the lines of force represent both magnitude and direction, they are spaced from each other in such a manner that the number of lines passing through a unit area of a surface at right angles to the field is always equal to the product of e_o and E. That is, for a unit area of surface

Number of lines = e_o X E (20)

... where e_o is K/4 pi ^2 and E is field intensity. Applying this definition to any area A, we have: Number of lines = e_0 EA (21)

A point charge produces lines of force having an outward radial direction. If such a charge is placed at the geometric center of a sphere of any radius, each line of force will pass through the spherical surface perpendicularly, thus fulfilling the conditions set forth above. Let the radius of the sphere be r; then the field intensity at every point on the spherical surface due to the point charge q is:

E = q/4 pi e_0 r^2

(Equation 19) and the total number of lines passing through the sphere is given by Equation 22, because the surface area of a sphere is 4 pi ^2

Number of lines = q (22)

The conclusion to be drawn from this analysis is that the number of lines that pass through a sphere concentric with a point charge is exactly equal to the magnitude of the point charge. Since the radius factor cancels out, it is evident that the same number of lines of force pass through every sphere containing a charge q at its center, regard less of the radius.

Lines of force are continuous, each one being terminated at one end by a positive charge and at the other by a negative charge.

This characteristic of continuity leads to an important generalization, originally stated by Gauss and known as Gauss' Law.

The net number of lines of force that leave a closed surface containing an electric charge is equal to the net positive charge inside the surface. If there is no net charge inside the surface, the net number of lines crossing the surface is zero.

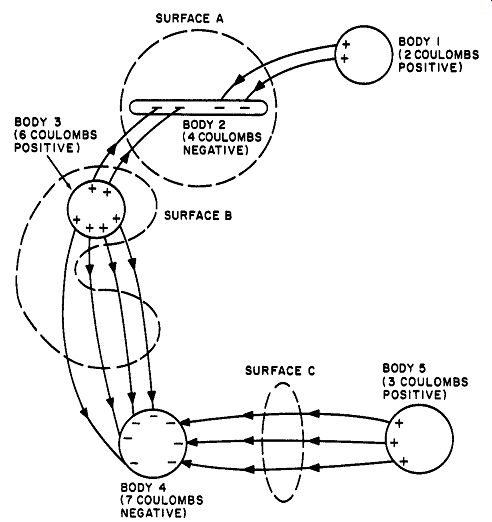
Fig. 13. Illustration for an application of Gauss Law.

The meaning of "net" when referring to charges, means the difference between the number of positive and the number of negative charges (or their algebraic sum). When referring to lines of force, the net number of lines crossing a 'Surface is equal to the algebraic sum of the lines passing outward through the surface and the number of lines passing inward through the same surface.

An application of Gauss' Law is shown in Fig. 13. Correlation between the number of positive and negative charges, the number of lines of force, and Gauss Law may be obtained from this figure as follows.

(1) Starting with charged body I, two positive charges (2 coulombs)

give rise to two outward-moving lines of force, which terminate on two negative charges on body 2. Thus two lines enter or cross surface A on this side.

(2) Two lines cross the other side of the surface A boundary, coming from two of the six positive charges on body 8, again going inward.

This makes a total of 4 lines entering surface A which, according to Gauss' Law, is equal to the four negative charges inside of surface A residing on body 2. This gives us an important corollary:

The net number of lines of force that enter a closed surface containing an electric charge is equal to the net negative charge inside the surface.

(3) Body 8 has 6 positive charges. Surface B is intersected at 12 points.

Of these, 9 lines intersect the surface going outward, while 8 intersect going inward, making a net of 6 lines going outward. Again, this corresponds with the number of positive charges in surface B in accordance with Gauss' Law.

(4) Surface C has no charge within it at all, hence the net crossings should total to zero. As seen, three lines from body 5 enter and leave the surface leaving a net of zero. Since surface C has no charges inside it, no lines can terminate within it.

(5) Because all lines must terminate at a positive charge at one end and a negative charge at the other, there must be an equal number of positive and negative charges if the representation is to be correct.

There are 11 charges of each sign in Figure 13, so that the number and direction of the lines conform with the theoretical requirements.

18. Examples of the Use of Gauss' Law

Gauss' Law may be applied to many different surfaces for the purpose of calculating the field intensity that results from various charge distributions. It may also be used to test certain basic assumptions that are taken as self-evident, such as the distribution of charge and the field is a conductor.

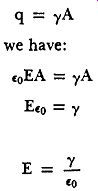
The Field Surrounding a Charged Sphere. A sphere of radius r1 is shown in cross section in Figure 14. Surrounding this conducting sphere is a second sphere of nonconducting material having a radius r2. The inner conducting sphere carries a positive charge of q coulombs uniformly spread out on its surface. With this symmetrical charge distribution and geometry, the lines of force may be considered to be directed outward radially from the inner sphere. Because the outer sphere is concentric with the inner sphere, all the lines of force that cross it must do so at right angles to its surface. From Equation 21 we have Number of lines Eo EA and for a sphere of radius r1 Number of lines = EoE (4 pi I^2)

By Gauss' Law, the number of lines leaving the sphere must equal the net positive charge within it, hence: q = EoE (4 pi I^2)

Solving for E: E

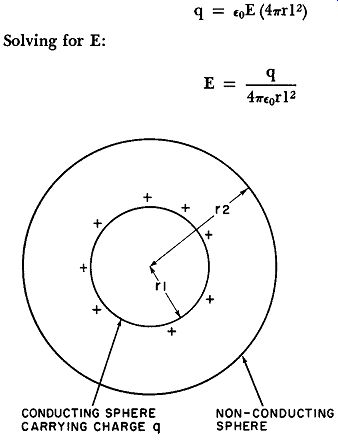
Fig. 14. Study of the field intensity around a charged conducting sphere.

It will at once be observed that this expression is identical with that previously derived for the intensity of the field at a distance r from a point charge (Equation 19). This means that the field intensity surrounding a charged sphere is the same as that of a point charge of the same total magnitude and that the charge on the sphere may be considered to be concentrated at its geometric center. As a second implication, the net field inside the sphere is zero.

The Field Within a Conducting Surface. We have shown in Section 4 that charges placed on a conducting surface tend to move as far apart as possible, due to mutual repulsion. Using Gauss' Law, we can now test this idea more rigorously.

Electrons in a conductor are free to move. If an electric field is present in the conductor, there will be motion of the free electrons as long as the field exists; conversely, the electronic motion will be zero if there is no electric field. As a corollary we may then conclude that we may assume the field in a conductor to be zero if the electrons are quiescent.

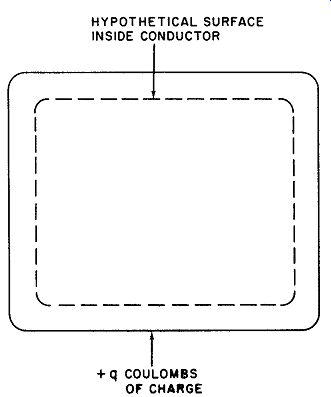
Fig. 15. Gauss' Law applied to a conductor.

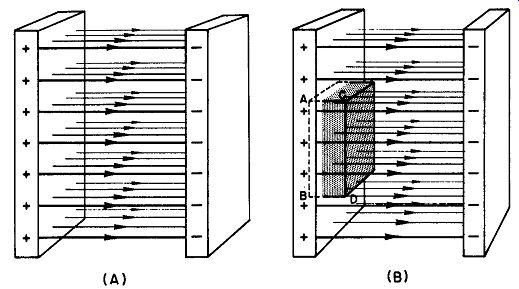
Fig. 16. Study of the field between two conducting plot.

Consider now a three-dimensional conducting solid (shown in cross section in Fig. 15). A charge of q coulombs has been placed on the conductor. From Gauss' Law, we may at once state that the net number of lines of force crossing any surface located an infinitesimal distance inside of the outer boundary of the conductor, such as the surface shown by the dashed line in Fig. 15, must be equal to the net positive charge within the surface. These charges are static. Since there is no motion of charges, the field within the conductor must be zero and the number of lines of force crossing the hypothetical surface must also be zero. In accordance with Gauss' Law, however, the net charge in the conductor must be equal to the number of lines of force crossing the surface in an outward direction. Thus, the net charge inside the conductor must also be zero. Because a charge of q coulombs was placed on the conductor initially, all of the charges must be located between the hypothetical surface and the outer surface of the conductor. Having originally assumed that the hypothetical surface was located an infinitesimal distance inside the conductor, we must conclude that all the charges are present on the outside of the conductor.

The Field Between Two Parallel Conducting Surfaces. If two parallel conducting surfaces (Fig. 16) are charged to equal magnitudes, but with opposite sign, the electric field between them consists essentially of straight lines of force uniformly spaced and parallel to each other. To use Gauss' Law for the determination of the magnitude of the electric field between the plates, let us imagine a closed surface having a rectangular cross section placed between the plates as shown in Fig. 16B. Side AB of this surface lies inside the conductor on the left, whereas side CD is outside the conductor and within the electric field.

Since there is no electric field in the conductor at the left (see the preceding example), there are no lines of force passing through side AB of the closed surface. Hence, the net number of lines of force passing through the closed surface are those that emerge through side CD. To determine the number of lines involved in this transition, we shall again use Equation 21.

Number of lines = e_o EA

… in which E is the intensity of the electric field between the plates and A is the area of side CD of the closed surface.

The total charge inside the closed surface is equal to the area A of side AB that encases the charges on the conducting plate multiplied by the charge per unit area on the plate itself. If y represents the charge per unit area, then:

q = yA

Applying Gauss' Law, we have:

e_o EA = yA

Hence or (23)

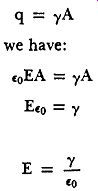
(24)

(25)

Hence, the field intensity in newtons per coulomb between two parallel, oppositely charged plates is equal to the number of coulombs per square meter of charge on either plate divided by the constant:

e_o ( e_o = 8.85 x 10^-12 coulomb^2/newton – meter^2)

Example: The field intensity between two parallel electrodes is 30,000 newtons per coulomb. An electron placed in this region will be acted upon by a force that moves it toward the positive plate. Calculate the magnitude of this force in dynes, assuming the charge on an electron to be approximately 1.6 X 10^-19 coulomb.

Solution: Find first the force on the electron in newtons.

F E = q F = Eq F = 3 X 10^4 X 1.6 X 10^-19

E = 4.8 x 10^-15 newton

Since there are 10^5 dynes in one newton, F = 4.8 X 10^-10 dyne.

Example: The charge on a sphere is 10^-3 coulomb, distributed evenly over its surface. Calculate the field intensity in newtons per coulomb at a point outside the sphere, 5 meters from the center.

Solution: Use Equation 19. E--q_

- 411'E or 2

E = 10^-3 4 X 3.14 X 8.85 X 10^-12 X 25 10^-3

E=---- 2779 X 10^-12

E = 3.6 X 10^5 newtons per coulomb

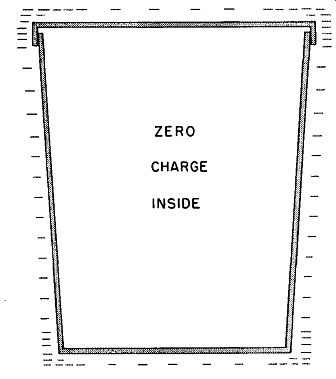
Fig. 17. A charged closed pail.

19. Distribution of Charge

Experiments conducted along the lines of Faraday's "ice-pail" investigation bring to light a number of important facts concerning the manner in which electric charges distribute themselves on conductors of various shapes.

The distribution of an electric charge may be examined by means of a metal disc mounted on an insulating handle and called a proof plane. If the disc is placed against the surface of the charged and insulated pail shown in Fig. 17 and then removed, it takes with it a portion of the charge, which may then be tested by means of an electroscope. The experiment proves that the greatest charge is obtained from the outer surface of the pail near its upper edge and on the outer corner of the bottom. Less is found on the middle of the cylindrical sides and none at all in the interim; if the pail has a metal cover. The absence of charge on the inside surface of a closed conductor was discussed in Section 4. The heavy concentration of charges on the corners of the pail leads to the conclusion that the greatest density of charge is found at points of sharpest curvature.

Charge density varies inversely with radius of curvature.

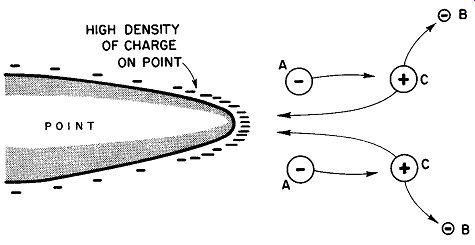
Fig. 18. The process of point discharge. (A) A negative ion is accelerated by the strong electric field near the point due to the point's high charge density. (B) Electrons dislodged from neutral gas molecules due to collisions with the accelerated Ions, leaving positive ions (C), which move toward the point.

When the density of charge exceeds certain limits, the air in the neighborhood of a charged surface is made slightly conducting by a collision process involving charged gas molecules with uncharged ones. This process is called "ionization." The strong electrostatic field around a sharp point accelerates any ions already present due to the effect of cosmic rays, etc. These ions collide with neutral molecules, often dislodging additional electrons. This leaves the gas molecules positively charged, and they move either toward or away from the point, depending upon the charge on the point. In either case, there are enough charged atoms of opposite sign to be attracted to the high charge density, where they pick up an excess of charge and are immediately repelled. It is found, therefore, that charges "leak" from sharp points much more rapidly than they do from surfaces of larger radius or curvature. The process is shown in Fig. 18.

Point discharge explains the efficiency of certain types of lightning rods, which enable a residence or other building to maintain itself in a more or less neutral electrical state by discharging through the sharp points. The phenomenon also explains why points must be avoided in high voltage power supplies such as those used in television receivers. Unless all connections are rounded, energy is lost through the effects of corona, another name for electrical discharge through ionized air.

20. Millikan Method of Measuring Electron Charge

In 1913, Robert Millikan reported on a series of painstaking experiments which established that the electron possesses a unique, indivisible quantity of electricity. Millikan's measurements also established the value of this quantity with high precision. His method, known as the "oil drop" experiment, was carried on as follows: A fine spray of oil is blown into a chamber (Fig. 19). The droplets settle toward the bottom of the chamber with varying speeds, depending chiefly upon their size. The surface tension of the droplets causes them to take on a spherical shape and they fall through the viscous medium (the air in the chamber) at a speed determined by the equation called Stokes' Law:

v= w / 6 pi rZ (26)

... where v is the final velocity of fall, w is the net weight of the particle after accounting for buoyancy, r the radius of the falling sphere, and Z is a constant that depends upon viscosity of the medium (coefficient of viscosity).

Sooner or later, one of the droplets falls through the small hole at the bottom of the chamber. As soon as one does so, the hole is closed and the single droplet finds itself in a region between two accurately spaced parallel plates across which a potential of several thousand volts is connected. The droplet is highly illuminated by the light of a carbon arc lamp, from which the heat rays are removed by a filter to prevent convection currents from affecting the experiment. An observing microscope is focused on the space between the plates and the movement of the drop is measured with respect to two pairs of cross-hairs. The time required for its passage from one to the other of the cross-hairs is precisely measured by means of a stopwatch, hence the speed of the droplet may be easily computed. This speed is a function only of the diameter and weight of the droplet and the viscosity of the air in accordance with Stokes's Law (Equation 26). In its passage through the chamber, each droplet takes on a small electric charge due to contact and induction effects. Assume that the droplet being observed carries a negative charge. As it approaches the lower plate, the switch is closed thus establishing an electric field in the space between the plates. Since the lower plate is negative, the droplet will begin to move upward in the field and again pass the cross-hairs of the microscope, this time at a different velocity.

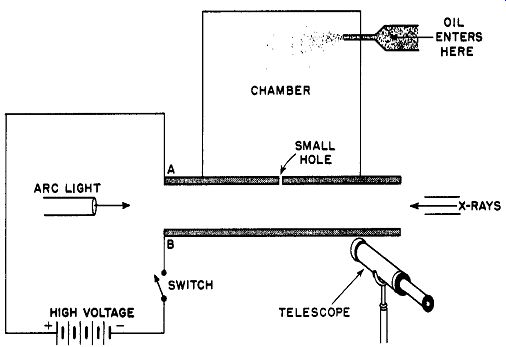
Fig. 19. The apparatus for the Millikan all-drop experiment.

At this instant, an X-ray tube at the opposite end of the plate area is momentarily flashed, causing the air in the vicinity of the droplet to become ionized. The droplet then may pick up or lose electrons and thus change its net charge which, in turn, causes a modification of its velocity and possibly direction of motion. The change in motion may be the result of a change of charge amounting to one, two, or more electrons lost or gained, but in any case the gain or loss must be equal to a whole number of electrons.

By thus watching and measuring the velocity of a single droplet often for hours at a time, Millikan found that no matter what the size, material, or original charge of the droplet, the change in charge was always a whole number multiple of 1.591 X 10^-19 coulombs.

Thus, the value and uniqueness of the charge of an electron were established.

21. The Oil-Drop Equations

The experimental procedure just described may be translated into appropriate equations that provide the actual value of the charge of an electron in terms of the experimental data.

Let v0 designate the steady-state velocity of an oil droplet when the electric field is not present and v the upward velocity of the same droplet under the influence of the field. Stoke's Law may then be written for these two conditions as:

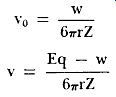
(27)

(28)

As before, Z is the viscosity of the air, E is the electric field strength in the region of droplet movement, w is the weight of the droplet, r is its radius, and q the absolute charge on the droplet. The numerator of Equation 28 is the net force acting on the droplet. (It is positive when it results in upward motion against the action of gravity.) For simplicity, the effect of the buoyancy may be neglected with out introducing serious error. If Equations 27 and 28 are added algebraically, the w factor drops out and the resulting equation may be solved for the charge on the droplet. Thus: Solving for q:

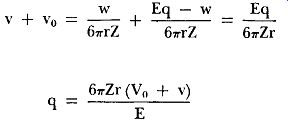
(29)

All of the quantities on the right side are directly measurable except the value of r, the radius of the droplet. The viscosity coefficient Z may be obtained by several precise methods, v0 and v are determined by observation with the viewing microscope, and the electric field intensity E may be easily obtained from the voltage between the charged plates and their separation, as will be shown in a later paragraph. The radius r must, however, be determined indirectly. The droplet is spherical due to surface tension, and the oil of which it is formed has a measurable density D. Thus, since density is defined as mass per unit volume,

1 w = VDg (30)

... where V is the volume of the droplet, D is the density of the oil, and g is the gravitational acceleration.

The volume of a sphere is given by V = 4/3 pi r^3 Substituting for V in Equation 30: w = 4/3 1rr3Dg

(31)

(32)

This value for w may be substituted in the form of Stokes' Law for the velocity v0 in the absence of a field (Equation 27),

Solving for r2 and taking the square root of both sides,

Substituting this value of r into Equation 29,

This expression may be rewritten as:

(33)

(34)

(35)

(36)

[From Equation 6, w = mg. The total mass of the drop is equal to the product of its mass per unit volume and its volume. ]

Now everything on the right side of Equation 36 is experimentally determinable. It was by observing the difference in the various q's calculated in this way for the same droplet that Millikan arrived at his conclusions concerning the uniqueness and value of the electronic charge, e. The best of modern determinations gives a value of e equal to 1.6018 x 10^-19 coulomb, which varies only slightly from Millikan's value.

22. Dielectrics

Conductors and insulators were touched upon in Section 3. In conductors, the electrons are not tightly bound to their atomic nuclei and are able to pass freely from atom to atom. In insulators, the bond is much tighter and a substantial voltage is needed to cause electron movement. Because the difference between conductors and insulators is one of magnitude rather than mode of behavior, the term insulator is relative and applies to the properties of the medium with respect to current conduction. When the behavior of an insulating medium is analyzed relative to its dielectric properties, i.e. number and density of electric field lines, resistance to electric breakdown, etc., the medium is called a dielectric. The behavior of a given substance when used as an insulator may be very different from its behavior when applied as a dielectric.

For instance, air is one of the best insulators known; in the dry state, its conductivity is very low even under the stress of large volt ages. Yet, as a dielectric it has a relatively low breakdown threshold, flashover occurring at about 75,000 volts per inch of gap. Rubber in comparison can withstand better than 400,000 volts per inch of dielectric thickness, but is not nearly as good an insulator as air, permitting leakage currents to flow under conditions at which air would stop them completely.

The ability of a substance to withstand breakdown is known as its dielectric strength. This characteristic is expressed in volts per unit thickness when the substance is placed between flat electrodes with rounded edges. Thus, the dielectric strength of air is 3,000 volts per mm, that of rubber is 16,000 volts per mm, and that of varnished cambric about 32,000 volts per mm. Modern ceramic and synthetic plastic dielectrics have even higher ratings.

The change in potential per unit thickness applied across a dielectric is called the potential gradient. For instance, 48,000 volts impressed across 30 mils of dielectric material establishes a potential gradient of 1,600 volts per mil. Potential gradient is always expressed in terms of voltages that are well below the breakdown potential, since, after a discharge occurs, there is likely to be charring or cracking of the insulating material, with a consequent change of all its dielectric properties in the area of the breakdown.

23. The Dielectric Constant

In restating Coulomb's Law (Section 17) mention was made of the constant K as the dielectric constant of the medium. Let us now define this term. When a d-c voltage is applied to two flat electrodes separated by a gap, a charge of +q is found on one and a charge of -q is found on the other. Should a slab of glass or polystyrene be now inserted in the gap, without altering the applied voltage, the quantity of charge rises to +q' and -q'. The increment in charge must, therefore, be due entirely to the presence of the new dielectric material. Thus, the dielectric constant of any insulating medium is defined as the ratio of the charge with an air (or more precisely vacuum) dielectric to the charge with the material dielectric without change of applied potential or: dielectric constant q q' (37)

The dielectric constants of several common insulators are given in the chart below.

DIELECTRIC CONSTANTS

Air .... 1

Water 81

Bakelite . .4.5 to 5.5

Polystyrene .. 2.5 to 7.5

Glass ..... .4.0 to 10.0

Porcelain 5.7 to 6.8

Paraffin .. 2.3

Mica .. 5.4 to 8.0

Rubber .. 2.0 to 2.5

24 QUIZ

1. Explain why lines of force between two conducting surfaces must intersect the surfaces at right angles.

2. Why is it convenient to discard the constant K originally used in Coulomb's Law in favor of a new constant e_0?

3. Define electric field intensity in words and in the form of an equation.

What are its units in the cgs system?

4. Prove that the same number of lines of force must pass through the surface of a hollow sphere of any radius if it contains a charge q at its center.

5. What is the convention regarding the direction of an electric field produced by a point charge q if the point charge is positive? if it is negative?

6. State Gauss' Law. If K in Coulomb's Law had not been replaced by e_o, how would Gauss' Law be stated?

7. Calculate the intensity of the electric field surrounding a sphere of 10 cm radius at a distance of 25 cm from the sphere if the charge on its surface is 2 coulombs.

8. Compute the field intensity between two parallel oppositely charged plates each of 100 cm^2 area. The charge on each plate is 0.5 coulomb.

9. Explain the effect of points on a charged body. Define the terms ionization and corona.

10. Describe qualitatively the method used by Millikan to obtain the charge on an electron.

11. Define dielectric strength and dielectric constant.