1. Introduction
The word transformer has different meanings in different fields.
For example, one college physics text defines a transformer as "a device used to change an alternating potential difference from one value to another." An industrial electronics guide states that "any two coils arranged in a way such that they have mutual inductance with respect to each other can be called a transformer." A recent secondary school guide on electricity refers to a transformer as a device "having a primary and secondary coil with a common laminated iron core." Finally, a radio textbook defines a transformer as a device in which "two or more coils are arranged so that energy may be transferred from one circuit to another by electro magnetic induction." Of these definitions, the last is the most general and inclusive.
Accepting this definition, it is logical to divide transformers into types, each classification based upon application. The radio engineer thinks of transformers in terms of air-core or powdered iron types. He often intentionally places two coils so that only a small fraction of the magnetic field produced by one coil passes through the other. These coils are loosely-coupled. The power engineer is concerned only with iron-core transformers, since his interest lies in obtaining a very high degree of coupling. He would like to have all the magnetic lines produced by the current in one coil linked with the second coil. On the other hand, an engineer interested in general electronics deals with all types of transformers--from loosely-coupled air-core types, through the various degrees of coupling found in intermediate-frequency (i-f) transformers, to power transformers having almost 100% linkage.
Theoretically, the degree of coupling or the fact that one transformer has an iron core while another has an air core makes little difference in the mathematical treatment. The same fundamental mathematical laws apply to both. Nevertheless, it has been found that specific methods of approach are more suitable for one case than the other. Therefore, we shall separate iron-core transformers from non-iron-core transformers in our treatment. Since we begin with iron-core types, we will review the fundamental facts and equations involved in magnetics that apply to such transformers.[ For a more detailed discussion of magnetism, see Advanced Magnetism and Electromagnetism edited by Alexander Schure. John F. Rider Publisher, Inc., 1959. ]
2. Flux Density and Magnetic Intensity
The magnetization characteristics of an iron-core transformer must be analyzed in terms of the two factors that cause consider able confusion-H, the field intensity (or magnetic intensity) and, B, the flux density or magnetic induction. To gain first a qualitative concept, consider the following. When a magnetic substance like iron is placed in a magnetic field, the iron becomes magnetized because it is ferromagnetic in character. As a result of this magnetization, the number of lines of induction within it (the flux density symbolized by B) is greater than the number of lines of force (the magnetic intensity symbolized by H). The difference between B and H for any given case is determined by the characteristics of the particular sample of iron in the magnetic field.
If the iron is highly ferromagnetic, the ratio between B and H will he large. If the iron is of poor magnetic quality, due to impurities, the ratio of B to H will be small. It follows, therefore, that we may describe the nature of the iron by the statement: B " = H (1)
in which µ is a constant for a given sample and is known as its permeability. Thus, in any given magnetic substance there are µ times as many lines of induction as there are lines of force. The constant µ, therefore, is a symbol that represents the ease with which a material can be magnetized.
3. Review of Magnetic Units
Although the mks (meter-kilogram-second) system of measurement is superior to the cgs (centimeter-gram-second) system in many important ways, the cgs system is encountered in many modern textbooks and papers. Therefore, we shall review the details of both systems and discuss the conversion factors that permit transfer from one system to the other.
Magnetic Field Intensity (H). The intensity of a magnetic field is measured by the force it exerts on a unit pole placed in the field. In the cgs system, the unit of magnetic field intensity is the oersted. It is defined as the intensity of a magnetic field in which a unit magnetic pole is acted upon by a force of I dyne. In the mks system, the unit of magnetic field intensity is the ampere turn-per-meter. This unit is based upon the field intensity inside a solenoid of N turns and L meters long, having a current of i amperes flowing through its winding.
H = Ni/L (2)
It is evident from Equation (2) that a coil having, say, 100 turns and a length of 10 cm (0. 1meter) and a current of 1 ampere flowing in it would have a field intensity within its vacuum or air core of H = 100 x 1.0/0.1 = ampere-turns per meter.
Flux Density (B ). The unit of flux density in the cgs system is the gauss. The gauss is defined as a single line of magnetic flux extending perpendicularly through an area of I cm^2
In the mks system, the unit of flux density is the weber per square meter.
Magnetic Flux (phi). Lines of induction are referred to as magnetic flux. A single line of magnetic flux in the cgs system is called a maxwell. Thus, a gauss is a flux density of one maxwell per square centimeter. In the mks system, the unit of magnetic flux is the weber. This unit is related to the maxwell as follows:
1 weber = 10^8 maxwells (3)
Equation (3) permits equating the units of flux density so that we can obtain the relationship between gausses and webers per square meter. That is:
1 gauss = 10^-4 webers per square meter
Permeability (µ.). The units for permeability are obtained by solving Equation (l) for each particular system. In the cgs system, the unit for permeability is gauss per oersted. In the mks system,
µ. is measured in webers per ampere-meter. A useful set of con version factors may be written:
1 oersted = 1000/'hr ampere-turns per meter (3)
1 weber = 10^8 maxwells (4)
1 weber/meter^2 = 10^4 gausses (5)
1 gauss-per-oersted = 4 pi x 10^7 webers per ampere-meter (6)
4. Permeability of Free Space
In the cgs system, the permeability of free space (and very closely that of air at normal atmospheric pressure) is taken as one.
This means that a field intensity of one oersted produces a flux density in air of one gauss. Therefore, Equation (1) may be rewritten as: B = µ.H (7)
By convention, the permeability of free space is symbolized by u_o and therefore: (8)
Thus, the permeability of free space is I gauss/oersted. From Equation (6) it is evident that the permeability of a vacuum m the mks system is 4 pi X 10^7 webers per ampere-meter.
5. Relative Permeability
It is often convenient to speak of relative permeability, or the ratio of the permeability of a substance to the permeability of free space. That is:

u=u/u_o (9)
in which µ. is the permeability of the substance and u_o is the permeability of free space. Since both expressions on the right side of the equation are given in the same units, relative permeability is a pure number. For nonmagnetic materials, u_r approaches unity; for ferromagnetic substances, it often runs up into the tens of thousands.
Neither permeability nor relative permeability is constant for any specimen of magnetic material. Permeability depends upon the magnetic history of the particular specimen and the extent to which it is already magnetized at the time the measurement is taken.
Example 1. What is the relative permeability of a piece of iron in which a flux density of 1.5 webers/m^2 is produced by a field intensity of 1000 ampere-turns-per-meter.
Solution. First find the permeability of the iron in webers-per-ampere-meter using Equation (1) .
µ, = B/H
= 1.5/1000
= 0.0015 weber/ampere-meter
The permeability of a vacuum is 4 pi x 10 ^-7 weber/ampere-meter.
Substituting in Equation (9) :
µr 0.0015/ (4 pi X 10^-7) 1,200
Note that transformer "iron" cores (really a high grade of silicon steel or other special alloys such as Hypersil) have relative permeabilities ranging up to 10,000. An alloy such as Permalloy (78.5% nickel and 21.5% iron) is characterized magnetically by a relative permeability of over 80,000.
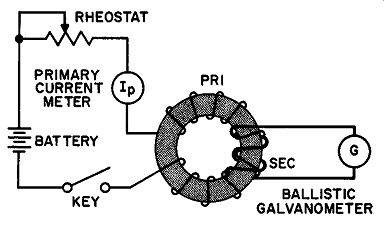
Fig. 1. Apparatus for obtaining the coordinates for the normal magnetization
curve.
6. Magnetization Curves
The inconstancy of the permeability of a ferromagnetic material is readily seen from the so-called normal magnetization curve. To obtain the coordinates for such a curve, the flux density B in the magnetic material is determined for various values of field intensity H. As a rule, the magnetic material to be tested is formed into a closed, doughnut-shaped toroid (often called a Rowland Ring) and wound with a primary and a secondary winding (Fig. 1).
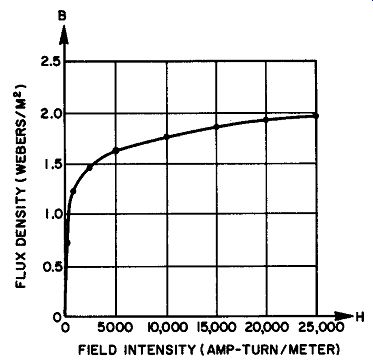
Fig. 2. The normal magnetization curve for ferromagnetic material.
When the key is depressed, the surge of current in the primary winding induces a secondary emf that causes a definite throw of the ballistic galvanometer. Starting with an unmagnetized specimen for each coordinate, the primary current is gradually increased (with the rheostat) and the throw noted for each value of current.
The field intensity H inside the specimen may he shown to be proportional to the primary current, while the flux density is proportional to the galvanometer throw. The normal magnetization curve is then obtained by plotting these points, as shown in Fig. 2.
The normal magnetization curve shows that the ratio of B/H, or the permeability of the specimen, remains constant with small field intensities as the flux density rises from 0 to about 1 weber/m^2. Beyond this, the permeability drops sharply, then gradually de creases for higher values of field intensity. As the field intensity is increased beyond 25,000 ampere-turns/meter (not shown in the graph), the specimen approaches saturation, a condition in which further increases in H do not yield corresponding increases in B. Figure 3 shows the curve of flux density vs field intensity required to change the magnetization of a material between two values of flux density B1 and B2. A curve of this kind is known as a hysteresis loop. The reverse field, necessary to reduce the flux density to zero, is called the coercive force. The flux density remaining in the material when the positive magnetizing field goes to zero (Br) is called the residual flux density.
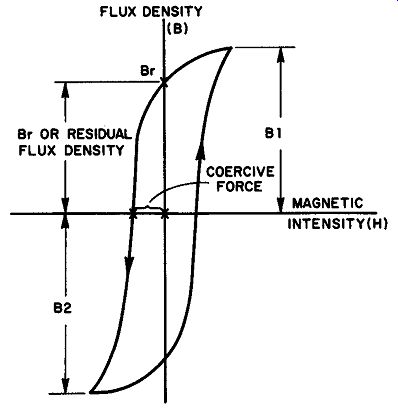
Fig. 3. A hysteresis loop.
The retentivity of the magnetic substance is defined as the flux density remaining after a saturating field has acted upon it. Materials with high retentivity are called magnetically hard and are suitable for use as permanent magnets.
If the retentivity is low, the material is magnetically soft and is usable as core material in chokes and transformers.
7. Core Losses
In the operation of any iron-core device, core losses occur in two ways. Core losses are largely responsible for the efficiency reduction of an inductive unit such as a transformer or choke and it is essential that they be kept minimal.
As alternating current passes through the windings of a transformer primary, with each reversal of current, the magnetic domains in the core material must re-orient themselves. During these current reversals, the flux density follows the hysteresis loop characteristic of the particular core. Since the domains offer opposition to re-orientation, energy that does not appear in the secondary circuit is consumed in the core substance. This energy loss is known as a hysteresis loss.
When the core material is soft, its retentivity is small. Similarly, the coercive force required to bring the flux density back to zero is small. Both these effects result in a diminution of the area enclosed within the hysteresis loop. If the area of the loop could be reduced to zero, the hysteresis loss would vanish, since both the residual flux density and the coercive force would disappear. Analysis has shown that the actual value of the hysteresis loss was directly proportional to the loop area.
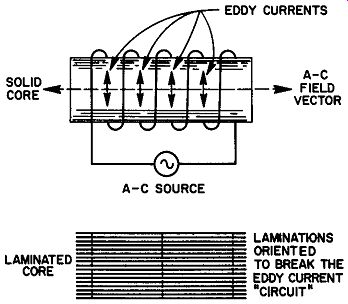
Fig. 4. A laminated core restricts the flow of eddy currents by breaking the
electrical circuit at right angles to the changing magnetic field.
When iron-core devices operate normally, the hysteresis loss is the same for each a-c cycle, regardless of its frequency. Thus, as the frequency increases, the hysteresis loss grows in the same pro portion. Therefore, to keep hysteresis losses at a low level, the core material must be sufficiently soft so as to have a small area loop and the frequency must be relatively low. At 60 Hz, the losses in ordinary transformer "iron" cores are tolerably low; but, at 400 Hz, they may increase to the point where operation is no longer feasible. It is for this reason that special core materials are used in 400 Hz equipment. The development of special core alloys such as HYPERSIL has done much to solve the problem of core losses at high frequencies. The permeability of HYPERSIL is approximately one-third higher than the usual silicon steels at comparable flux densities.
As the alternating field reverses polarity, a second type of core loss results from the flow of randomly induced currents in the core materials. Eddy current loss, as it is called, represents a waste of energy due to the I^2 R power consumed in the core where it cannot appear as useful output in the secondary circuit. Eddy currents flow at right angles to the changing flux since maximum emf is always induced in a conductor perpendicularly to the direction of the field. The use of thinly laminated core material (each lamination is insulated electrically from the adjacent one by shellac, varnish, or an oxide scale) can reduce eddy current losses to a reasonably low figure. Because the induced currents in the core flow at right angles to the field, the laminations are always oriented parallel to the field, as shown in Fig. 4.
Both theoretical and practical considerations permit us to develop an equation whereby eddy current loss in watts can be calculated.
f2B2t Loss= k -R-- (10)
in which f = a-c frequency in coil winding, B = a-c flux density, t = core lamination thickness, R = resistivity of the core material, and k = proportionality constant dependent upon the units used in the equation. From Equation (10) , it is evident that eddy current losses in a given transformer are directly proportional to the square of the frequency, the square of the a-c flux density, and the average thickness of each lamination; and are inversely proportional to the resistivity of the core material.
8. Measurement of Core Losses
Measurement of total core loss (i.e., the sum of both hysteresis and eddy current loss) is not difficult. With the secondary circuit open, the rated primary voltage (at the rated frequency) is applied, and the power input of the transformer measured across the primary winding with a wattmeter. For this condition, the losses in the transformer consist of the primary copper loss (I^2 loss in the primary wire) and the core losses.
The primary resistance is then obtained with an ohmmeter and the primary current measured with an ammeter. The sum of the hysteresis and eddy current losses is the difference between the losses, as obtained with the wattmeter and the calculated copper loss.
To individually determine the hysteresis and eddy current losses, a power source whose voltage and frequency are both variable must be available. The procedure is as follows:
A. The sum of the core losses is obtained by the method described above, but the transformer must be loaded to its rated secondary current, so that the flux density in the core is as specified by the manufacturer.
B. The core loss at several lower frequencies but at the same flux density is then determined. The flux density can be maintained at a constant value, by reducing the applied voltage in the same proportion as the frequency is reduced. Since the flux density is inversely proportional to the frequency of the applied emf, reducing the voltage in step with decreasing frequency results in uniform flux density throughout the test.
C. The core loss per cycle is then plotted against frequency, with core loss handled as the dependent variable, and plotted on the Y-axis of the graph.
D. The next step involves extrapolating the curve to zero frequency. The core loss per cycle at zero frequency is the hysteresis loss per cycle for the particular value of B maintained during the measurement. Eddy current losses vanish at zero frequency, since there cannot be induction without a varying magnetic field. On the other hand, residual flux and coercive force still exist, so that hysteresis loss at zero frequency has a very definite meaning.
E. The hysteresis loss at the normal operating frequency is then obtained from the product of the hysteresis loss per cycle and the frequency normally used.
F. Finally, the eddy current loss is determined by subtracting the hysteresis loss at the normal operating frequency from the total core loss as obtained in Step A.
G. Current and Voltage Waveforms in Transformer
Primaries In a well-designed transformer, it may be observed that, although the applied voltage may be perfectly sinusoidal, the primary current (secondary unloaded) is far from sinusoidal in waveform. This arises from hysteresis loss effects.
Considering the primary winding of the transformer as an inductance in series with an a-c generator, we may derive the relation ship given in Equation (11). eu is the generator voltage, R is the resistance of the winding, icf, is the exciting current in the inductance, and e, is the counter-emf developed in the coil.
e, = Rief,+ e1 (II) The induced voltage may be expanded, however, where N is the number of turns in the inductance, and dcf>/dt is the rate of flux change in lines per second.
_ N def> e, - 10^8 X dt (12)
If the transformer is well designed, its primary resistance will be quite small and the inductive reactance large enough to keep the induced current id> quite small. The product Ri¢ is normally very much less than the input generator voltage e0
This means that the induced voltage e1 will almost be the same as the applied voltage. Consequently, if e0 is sinusoidal, e1 will very closely approach the shape of a sine wave.
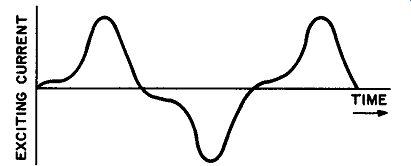
Fig. 5. Waveform of exciting current
In the primary winding of a well designed transformer.
From Equation (12), we see that the waveform of the varying magnetic flux in the core also is nearly sinusoidal, since the two are directly proportional. However, the shape of the hysteresis loop prevents a sinusoidal flux from being produced by a sinusoidal current. Hence, the exciting current is not sinusoidal, but has a shape similar to that shown in Fig. 5. This current comprises a component that is in phase with the induced voltage and a component that lags behind the induced voltage by 90°. The in-phase current component is generally referred to as the core-loss current; the out-of-phase component is known as the magnetizing current.
10. Transformer Shielding
A transformer shield is often necessary to confine the magnetic field to a given region of space, or to prevent the effects of the field from being felt in some other area. Stray magnetic fields induce hum voltages in audio equipment, produce feedback and instability in high-frequency devices, and otherwise give rise to undesirable coupling effects.
D-c and low-frequency fields are best diverted by a shield material made of high-permeability metals. The completed shield should form an unbroken magnetic path for the flux being diverted.
For this situation, the inductance of a given winding will be increased, because the shield represents a flux path of lower permeability than the air it replaces. This is especially true for high frequency air-core coils that have little inductance in the first place.
At intermediate frequency (i-f) and radio frequency (r-f) ranges, the most effective magnetic field is made of a good electrical conductor such as copper or aluminum. The varying magnetic flux passing into the metal induces eddy currents which, in turn, give rise to magnetic flux that opposes the entering flux (Lenz's Law) . The confining action in this case, therefore, arises from opposing force effects rather than from new paths created by a shield of magnetic material. An eddy-current shield should be carefully lapped and soldered (or welded) in construction, to reduce the overall electrical resistance to a minimum. An aluminum or copper shield has the opposite effect on inductance. It causes the inductance to diminish, because of the reduced permeability of the path provided by the shield.
Electrostatic shielding is generally less critical than magnetic shielding. Any metal, even one open-meshed, will, if it is carefully grounded, generally offer adequate electrostatic shielding. When individual transformer windings are to be shielded from each other, it is sufficient to wrap one layer of foil around the outside of the innermost winding and ground it at one spot. The wrap ping must be cut so that there is no overlap, since overlapping would cause a shorted turn.
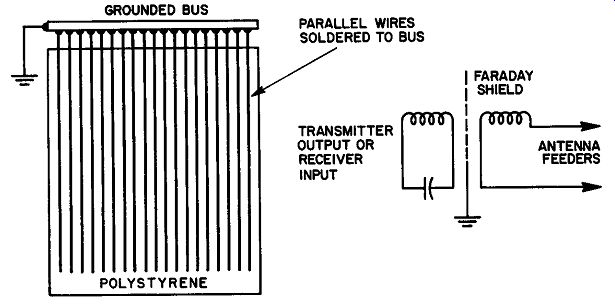
Fig. 6. A Faraday shield reduces capacitive coupling between the windings
of a transformer.
Frequently found between the windings of an inductively coupled antenna system is a special type of shield known as a Faraday Shield. Since harmonics are radiated (or received) largely by capacitive coupling between the antenna coil and the resonant circuit, minimization of harmonic effects may be accomplished by arranging the coupling so that it is entirely inductive. (See Fig. 6.) A Faraday Shield must be so constructed that there are no complete electrical paths through which eddy currents can flow. A typical approach to the problem is shown in Fig. 6. Bare wires spaced their own diameter apart are cemented to a polystyrene sheet in parallel rows. Then they are connected together electrically along one end by soldering them to a length of bus wire.
The bus wire is grounded to the common ground of the system on one side only.
11. QUIZ
1. Describe carefully the difference between flux density and magnetic intensity.
2. Define permeability in terms of flux density and magnetic intensity.
3. Review the meanings of the following units by defining each one and cataloging them in either the cgs or mks system: (a) oersted, (b) maxwell, (c) ampere-turn-per-meter, (d) gauss, (e) weber, and (e) webers-per-square-meter
4. For what medium does a field intensity of 1 oersted produce a flux density of I gauss? What is the permeability of this medium?
5. What is the permeability of a medium in which a field intensity of 1oersted gives rise to a flux density of 1,500 gausses?
6. What field intensity is required to produce a flux density of 4 pi X 10^-1 webers-per-square-meter in a core material having a permeability 64 pi x 10^7 webers-per-ampere-meter?
7. What is the relative permeability of a specimen of magnetic material in which a flux density of 6 webers-per-square-meter is produced by a field intensity of 2000 ampere-turns/meter?
8. What is meant by coercive force in a hysteresis loop?
9. Name and describe the source of core losses in transformers.
10. Describe a method whereby total core loss is determined. Expand this description to cover the determination of separate hysteresis and eddy current losses.
Also see: