High-Frequency Transformers

44. General Considerations

High-frequency transformers are most often used as coupling devices in electronic equipment where amplifier stages follow one another in cascade, or where a transfer of energy is to occur between a transmission line and a source or a load. A study of high-frequency transformers generally involves the following considerations: The transformer as a coupling impedance, the bandwidth of the coupling system, and the gain made possible by the use of the transformer. Frequently, the engineer is faced by problems that simultaneously involve all three of these factors.

Analysis of high-frequency transformers (or inductively-coupled circuits, as they are often called) involves a study of resonant and non-resonant primary and secondary windings in various combinations. Therefore, we consider examples in which neither winding is tuned, only one winding is tuned, and cases where both the primary and secondary windings are resonant. Furthermore, the behavior of high-frequency transformers is strongly dependent upon the coefficient of coupling between primary and secondary, insofar as this affects coupling impedance, gain, and bandwidth.

45. High-frequency Transformer-Neither Winding Tuned

Fig. 29. Untuned high-frequency transformer.

In many respects, the analysis of an untuned high-frequency transformer is so closely analogous to that of a low-frequency iron-core transformer that the equations are the same. For example, if the coupling coefficient is unity, and if the copper losses and distributed capacitance are close to zero, the voltage ratio will be the same as the turns ratio is in a power transformer. Since all of these conditions are never satisfied in practice, the determination of the behavior of an untuned high-frequency transformer must be handled by a somewhat different method. (See Fig. 29.) The primary and secondary windings have impedances of their own, z,, and Z,. The primary impedance, with zero load on the secondary (secondary open-circuited) consists of the resistance and inductance of the primary coil. When the secondary is open, the impedance of the entire secondary circuit may be considered to he infinite. For this condition, the secondary has no affect upon the primary winding and it behaves as though it were an isolated coil.

With a load connected across the secondary coil, current flows.

The resulting magnetic flux opposes the current in the primary winding and causes a new impedance to appear that was not present before secondary current began to flow. The effect of this inductive opposition is equivalent to adding an impedance in series with the primary winding. This impedance is known as coupled or reflected impedance. The value of reflected impedance is given by the expression:

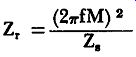
(40)

where Z, = reflected impedance in ohms, f = frequency in Hz, M = mutual inductance in henries, and Z, is the secondary impedance in ohms. There will be little reflected impedance if the coefficient of coupling is small, since in that case M is also small.

(The same is true if the impedance of the secondary is large.) As M grows, and as the load on the secondary decreases making Z, smaller, the coupled impedance becomes significant. As a result, the. voltage and current relationships in the primary are then substantially dependent upon the secondary characteristics. Also, a large transfer of energy from primary to secondary may occur under these conditions.

Fig, 30. High-frequency transformer with untuned primary end tuned secondary.

It is important to recognize the phase relationship between the secondary impedance and the reflected impedance into the primary.

Mathematical analysis shows that, although the phase angles are the same, the signs are reversed. For instance, if the impedance of the secondary circuit is inductive with a phase angle of 45 deg., the impedance coupled back to the primary circuit is also 45 deg. but is capacitive in phase characteristics. This sign reversal has an important bearing on the behavior of high-frequency transformers.

Note also that the coupled impedance will be a pure resistance, if the secondary impedance is a pure resistance. This case is particularly important when resonant circuits are analyzed since, in such circuits, the inductive and capacitive components cancel each other and leave purely resistive loads. (This will be considered later.) To describe another special case, consider what occurs when the secondary winding of an untuned high-frequency transformer is short-circuited. For this condition, the secondary circuit resistance is negligibly small compared to the secondary inductance. Thus, the coupled resistance may also be taken as zero and the only coupled impedance is capacitive. This serves to reduce the inductance of the primary to an extent limited only by the coefficient of coupling. Thus, for a unity-coupled circuit, the primary inductance is completely neutralized.

Untuned high-frequency transformers have little practical application in coupled circuits and are rarely used in electronic equipment. They merely form the basis for a more extended study of single- or double-resonant types.

Before going on to the frequently-encountered coupling circuits, let us investigate how a coil shield or a metal chassis or panel may important bearing on the behavior of high-frequency transformers.

A coil shield is a closed loop that may be considered to possess both inductance and resistance, and is inductively coupled to the coil that it shields. Since the inductance of the shield can is coupled back to the coil as a capacitance, it reduces the effective inductance of the coil. If the can has low resistance (as is true of copper and aluminum shields), the reflected resistance may be disregarded.

Thus, if the coil is part of a resonant circuit, as it usually is, the resonant frequency of this circuit will increase.

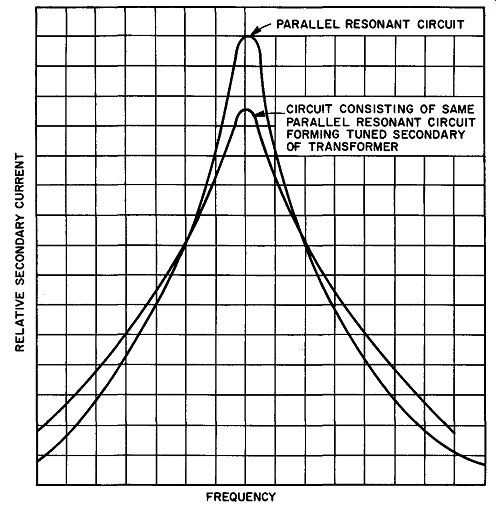
Fig. 31. Curves showing that the coupled impedance varies in a manner that is similar to the resonance behavior of a parallel-resonant circuit.

46. High-frequency Transformer with Untuned Primary and Tuned Secondary

Transformers with untuned primaries and tuned secondaries are often found in cascaded r-f and i-f amplifiers. (See Fig. 30.) The coupled impedance of this circuit is given by the same equation as in the case of the transformer with neither winding tuned (Equation 40) . When this equation is compared with the expression for a simple parallel resonant circuit, it is seen that both have the same form. Since the parallel impedance given in Equation (41) is definitely a function of frequency, it is clear that the coupled impedance is also a function of frequency.

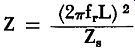
(41)

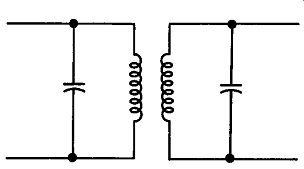
Fig. 32. A high-frequency transformer having tuned primary and secondary circuits.

Since the equations have the same form, the variation of coupled impedance must be considered to vary with frequency according to the same law that governs the variation of parallel impedance of the secondary circuit alone. When this is checked experimentally, the curves obtained appear somewhat as in Fig. 31. Note that the curves have the same general form but that the Q of the overall transformer response (the secondary current as a function of the reflected impedance) is somewhat less than the Q of the secondary taken alone as a simple parallel resonant circuit. The transformer curve was obtained in a circuit in which primary source resistance was appreciably greater than impedance of the primary winding.

From these curves, it is clear that a transformer with an untuned primary and tuned secondary may be used with excellent results as a selective coupling stage in electronic equipment.

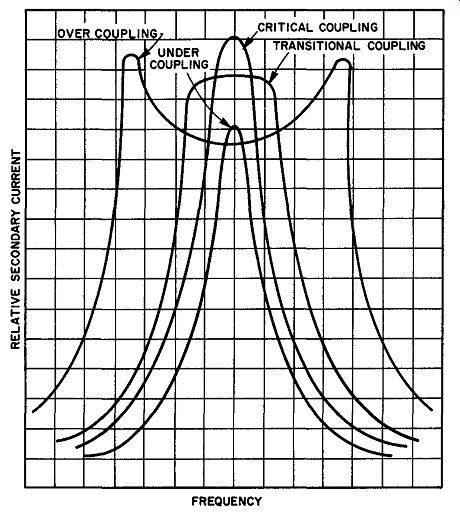
Fig. 33. Curves for various coefficients of coupling described in accepted qualitative terms.

47. Transformer-Both Windings Tuned

If the coefficient of coupling between a tuned primary and a tuned secondary is low (of the order of 0.007), the secondary current variation as a function of frequency follows very closely the curve given in Fig. 31 for a parallel resonant circuit, except that it may be somewhat sharper-its peak may not be as high.

As the coefficient is increased, the character of the secondary cur rent curve begins to undergo radical changes. (See Fig. 32.) In Fig. 33, we have presented four different curves, one for each of four different coupling conditions. Since actual coefficients have little meaning outside numerical problems, the qualitative terms under coupling, critical coupling, transitional coupling, and overcoupling have been used to describe the most commonly used coefficients. The curves shown in Fig. 33 were obtained from a tuned transformer in which both windings were resonant to the same frequency. In addition, both tuned circuits had the same Q. When the two circuits are tuned to slightly different frequencies, the curves retain the same shape, but drop somewhat in amplitude. If the Q's differ, the amplitudes of the peaks in the double-humped curves will be different.

48. Under-coupling

A tuned transformer in which both primary and secondary are resonant to the applied frequency is said to be under-coupled if, by changing the orientation of the two windings, it is possible to increase the secondary voltage. The gain of an under-coupled circuit is generally expressed as some value relative to the maximum possible gain that the circuit can provide.

Under-coupled circuits provide less gain than the circuit is capable of giving, but do have the advantage of giving the sharpest possible resonance. When i-f transformers are under-coupled, they are highly selective and are very useful in communications receivers where selectivity rather than bandwidth is important. If the coupling coefficient is much below the maximum-gain coupling, the shape of the secondary voltage response curve begins to approximate the product of the response curves of two circuits having Q's that are equal to the primary and secondary circuit Q's, respectively.

49. Critical Coupling

A tuned transformer is critically coupled if its windings have been oriented to obtain the maximum possible secondary voltage for a given input signal. Critically coupled circuits are encountered in the r-f and i-f stages of many high performance radio receivers.

50. Transitional Coupling

A tuned transformer is transitionally coupled if its windings have been oriented to yield the flattest possible response curve.

Transitional coupling provides the widest passband without double peaks, and is often referred to as optimum coupling. Transitional coupling is used in radio receivers where both a large bandwidth (as compared to under-coupled or critically coupled circuits) and high-gain are required. When properly adjusted, a circuit coupled this way provides excellent all-around performance. Thus, it is desirable for low cost, medium performance superheterodyne receivers, particularly those that are not necessarily to be used for speech frequencies only.

51. Overcoupling

A tuned transformer is over-coupled if the coupling coefficient is large enough to cause the secondary response curve to show a double peak. When both the primary and secondary circuits are of very high Q, the peak amplitudes tend to be equal. For low Q circuits, the low-frequency peak is larger and the high-frequency peak is smaller in amplitude. In both cases, however, the average height of the two peaks is very nearly the same as the amplitude of the curve, when the circuits are transitionally coupled.

A wide, flat response-such as one would want in a high-fidelity superheterodyne receiver-is often obtained from a two-stage i-f amplifier, where the double-peak response of an over-coupled transformer is added to the single-peak response of a transitionally coupled circuit. The over-coupled circuit must be symmetrically tuned about the response curve of the other stage. This response can be successfully obtained only by proper selection of both Q's, by careful alignment of the tuning, and by proper selection of the coupling coefficient.

52. Gain-bandwidth Factor-General

The value of an amplifier circuit is determined, in many in stances, by the amount of gain that can be obtained for a given bandwidth. This criterion is particularly true of video amplifiers and other wideband systems where bandwidth is a primary consideration. Obviously, the gain and bandwidth of an amplifier stage are determined by the tube, the high-frequency coupling system, and the values of other significant circuit components. Many engineers refer to the gain-bandwidth product (U) of an amplifier system, considering this number to be helpful in evaluating the performance of the circuit. The gain-bandwidth product is given by the expression:

U = voltage gain X bandwidth (mc). (42)

Thus, if a tube is capable of producing a gain of 12 in a circuit having a bandwidth of IO me, its gain-bandwidth product is 120 (U = 120).

Analysis shows that U for a simple resistance-capacitance coupled amplifier may be calculated from:

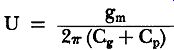
(43)

where g"' = transconductance of the tube, Cg = grid to ground capacitance of the following tube, and CP = plate to ground output capacitance of the tube in question. This shows that U depends upon the tube's transconductance and the capacitive spacing of its elements, as long as a coupled circuit does not enter into consideration.

When transformer coupling is used between stages, the gain bandwidth product is no longer merely a function of tube characteristics. It is strongly affected by the Q ratio of the two coils and by the relative values of the primary and secondary circuit capacitances. For this reason, the gain-bandwidth product as such is seldom used in inductively coupled circuits. Rather, a new element appears-the gain-bandwidth factor. This factor is utilized only to evaluate the performance of the coupled circuit and not the whole amplifier system.

The gain-bandwidth factor is defined as the ratio of the gain bandwidth product of a given circuit to the gain-bandwidth product of a single-tuned circuit that has the same circuit capacitance as the sum of the primary and secondary capacitances of the coupled circuit. A single-tuned circuit is defined as a parallel combination of one inductance, one capacitance, and one resistance. Thus:

(44)

in which F = the gain-bandwidth factor, Uc = the gain-bandwidth product of the coupled circuit, and u. = the gain-bandwidth product of the single-tuned circuit.

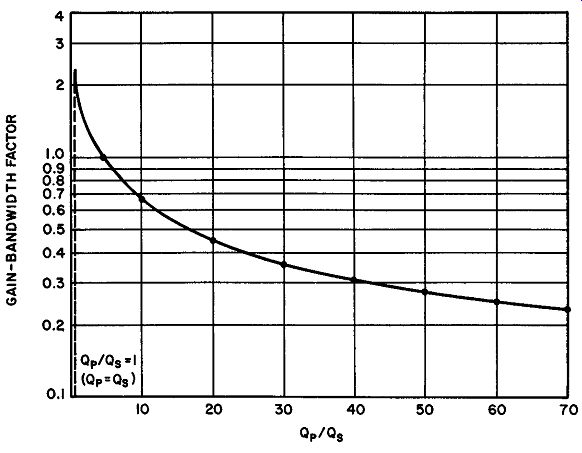
Fig. 34. Gain-bandwidth factor for critically-coupled circuit as a function of Qp/ Q8 , with CP = C8

53. Gain-bandwidth Factor for Critically Coupled Circuits

The gain-bandwidth factor in critically coupled circuits is greatest when Q.p = Q., and CP is either much larger or much smaller than C,. If the total primary capacitance equals the total secondary capacitance, then even when the Q's are equal, the gain-bandwidth factor is only 1.08. This is hardly a significant improvement over the performance of a single-tuned circuit. However, if either capacitance is made 10 times larger than the other, the gain bandwidth factor may rise to 1.88 for equal primary and secondary Q's.

The curve in Fig. 34 shows the variation of F for various Q ratios when C, = C,. To determine the gain-bandwidth factor when C, = C,, the F obtained from this curve must be multiplied by the correction given in Equation (45).

correction multiplier = Cp+C, 2yCPC• (45)

Example 7, Find the gain-bandwidth factor of a high-frequency, critically coupled amplifier circuit in which the primary-to-secondary Q ratio is 4.5:1, and in which CP = 50,.,.f and C8

= 10,.,.f.

Solution: Referring to Fig. 34, it is seen that the uncorrected value of F is equal to I. Applying the correction multiplier, we have:

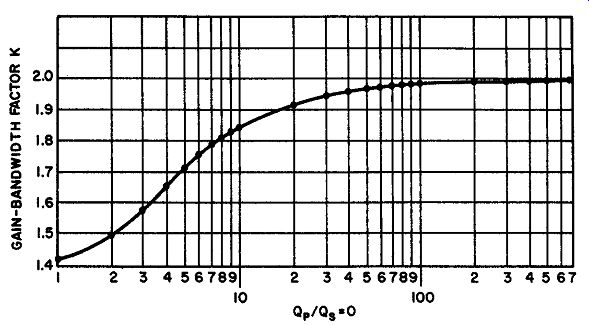
Fig. 35. Gain-bandwidth factor for transitionally-coupled circuit as a function of Qp/ Q8, with CP = C1

54. Gain-bandwidth Factor for Transitionally Coupled Circuits

Transitional coupling enables the circuit designer to obtain greater gain-bandwidth factors than is obtainable with critically coupled circuits. The same general rules for gain-bandwidth factor determination are followed with the help of the curve in Fig. 35.

The gain-bandwidth factor is first ascertained for a given ratio of primary-to-secondary Q, assuming equal primary and secondary capacitances. If they are not, the factor obtained from the curve is then multiplied by the same correction multiplier as was used for critical coupling (Equation 45) .

The curve shows that a gain-bandwidth factor range of about 1.42 to 2 is possible, with the higher values obtained when the Q ratio is large. As a comparison between the critically coupled circuit discussed in the last paragraph and a transitionally-coupled circuit having the same constants, note the solution to the following example.

Example 8. Find the gain-bandwidth factor of a high-frequency, transitionally coupled amplifier in which the primary-to-secondary Q ratio is 4.5: I, and in which Cp = 50µ.µ.f and c. = 10µ.µ.f.

Solution. The gain-bandwidth factor for equal primary and secondary capacitances is first obtained from the curve of Fig. 35, and then the correction multiplier is used. For a Q ratio of 4.5: I, the gain bandwidth factor is read from the curve as 1.69. Applying the correction:

F = 1.69 X 50X 10 / 2__/500 = 1.69 X 1.34 = 2.27

Note the substantial improvement in gain-bandwidth factor for a transitionally coupled circuit as compared with an identical critically coupled circuit.

Fig, 36. The ratio k as a function of the primary to secondary Q ratio, in a transitionally-coupled high-frequency amplifier.

55. Gain Ratio in Critically Coupled Circuits

Gain ratio (GR) is defined as the ratio of the gain of a stage coupled in a specific manner (critically or transitionally) to the gain of a single-tuned stage having the same total circuit capacitance, without regard for bandwidth. Ordinarily, both gain and bandwidth are important considerations; under certain conditions, however, voltage gain is the prime objective. In this case, we must examine the equation for gain ratio in critically coupled circuits, to determine whether or not such circuits are capable of more gain than a single-tuned stage. The equation is:

…in which Q = the Q of the comparative single-tuned circuit and the remaining symbols represent the same factors as before.

If C_P = C8, the correction factor (extreme right-hand term) is always unity. Since __/ (QpQs.) is not likely to be greater than the Q of a comparable single-tuned circuit, very little benefit (with regard to gain) can be realized by using a critically coupled double tuned circuit. To obtain a larger gain ratio in this type of stage, GP must be made as different from G8 as the conditions permit.

To summarize, the maximum gain-bandwidth factor and the greatest gain ratio taken together will provide the best conditions for high gain and wide bandpass. These conditions can be realized by making the primary-to-secondary Q ratio as close to unity as possible, and GP and G. as different as possible, without controverting limitations imposed upon the system by resonance and space requirements.

56. Gain Ratio in Transitionally Coupled Circuits

The gain ratio for a transitionally coupled circuit is given in Equation 47.

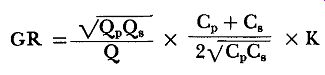
(47)

… where K is the ratio of the gain for transitional coupling to the gain of the same circuit for critical coupling.

For all conditions except a unity Q ratio, K is less than one. Therefore, the gain ratio of transitionally coupled circuits is generally less than that of critically coupled circuits. This follows logically since, except for the multiplier K, Equation (47) is identical with Equation (46) for critical coupling. For any practical circuit in which Qp and Q. are known, the value for K may be obtained from the curve in Fig. 36.

Example 9. Given the circuit characteristics below, first determine the gain ratio for a critically coupled circuit and then for a transitionally coupled circuit, as compared with a single-tuned circuit with a Q of 100.

Solution. For critical coupling

The voltage gain of a critically coupled circuit with these characteristics would be 0.582 times the gain of a single-tuned circuit.

For transitional coupling, the value of K for a transformer having a Q ratio of 100/30 or 3.33 is 0.92. Therefore, the gain ratio for a transitionally coupled circuit having is characteristics given is: K = 0.582 X 0.92 = 0.536 So that the voltage gain to be expected from a transitionally coupled circuit is somewhat less than that for the equivalent critically coupled circuit.

57. QUIZ

1. Explain why the bandwidth characteristics of a high-frequency transformer are often more important than its gain characteristics.

2. Define reflected (or coupled) impedance. Give the equation for reflected impedance in terms of frequency, mutual inductance, and secondary impedance.

3. Explain, in terms of coupled impedance, why the inductance of the primary of a transformer is neutralized when the secondary is short-circuited.

4. What is the principal advantage gained by using a double-tuned i-f transformer instead of a single-tuned type?

5. Distinguish carefully between under-coupling, critical coupling, transitional coupling, and overcoupling, in terms of the response curves of these systems.

6. What particular types of applications call for the use of transitional coupling? Overcoupling?

7. Define gain-bandwidth factor. How does it differ from the gain-bandwidth product?

8. Find the gain bandwidth factor of a critically coupled amplifier circuit having the following constants: Q ratio, P:S = 10, CP = 150µµf, and C6 = 100µµf.

9. Determine the gain-bandwidth factor for a circuit with transitional coupling, having the same constants as those in Question 8.

10. What is meant by gain ratio? How does the gain ratio of critically coupled circuits differ from that of transitionally coupled circuits having identical constants?