The clocks-around-the-world experiment of 1971 finally confirmed the "dilation of time" of relativity theory--or did it?
by W.A. SCOTT MURRAY
----------
Development of the cesium clock as a practical instrument led in 1971 to an experiment to verify Einstein's prediction of the "dilation of time", and its successful outcome helped to clarify certain aspects of interpretation in relativity theory. But a question remains: one prediction by Einstein concerning the relative rates of polar and equatorial clocks--has not been borne out in practice. It seems that the explanation which was originally put forward to account for this failure itself contains a flaw, so that the topic now requires a further round of attention from physicists and philosophers.
----------------
“... If one of two synchronous clocks at A is moved in a closed curve with constant velocity v until it returns to A, the journey lasting t seconds, then by the clock which has remained at rest the travelled clock on its arrival at A will be ½[tv^2]/c^2 seconds slow. Thence we conclude that a balance-clock at the equator must go more slowly by a very small amount than a precisely similar clock situated at one of the poles under otherwise identical conditions."
-Albert Einstein, 1905
----------------
Ever since that statement was first published, in the famous paper which launched Einstein's special theory of relativity, scientific opinion has remained divided as to whether its burden was either meaningful or true. Among those who have questioned it may be cited Lord Rutherford (who said in jest that Anglo-Saxons had too much sense to understand it), Herbert Dingle (himself a well-known supporter of the theory, turned renegade), and Louis Essen (a world-renowned authority on the practical definition and measurement of time). Among those who have accepted it without question must be listed every convinced Relativist, past and present, bar none.
Such overwhelming preponderance of talented opinion in its favor could not be gainsaid, were it not that the statement seems to contradict a premise of Einstein's own theory the Principle of Relativity.
Theory suggests that the clock on the equator may equally well be taken to be the clock "at rest", so that the polar clock must run slower than the equatorial clock by exactly the same amount.
This is one of several criticisms of relativity theory about which argument has persisted for some eighty years, and with good reason. Defense of the statement has taken on many forms: that Einstein was speaking figuratively and did not intend what he had written down so clearly in that paper to be interpreted in a literal sense; or that Einstein's result was correct but for the wrong reason, in that the example he gave referred to a rotating earth and hence required the general theory of relativity for its proper explanation; or, circularly, that since every physical test performed to date has confirmed the truth of the Special Relativity theory this example must also be true, and if we find it illogical--a "paradox"--it must be because we have failed to understand the theory properly: "Only paranoics question Relativity"!
It will also be claimed by cognoscenti that Einstein's statement has been proved by direct experimental measurement. Let us therefore examine the basis of that claim in detail.
HAFELE AND KEATINGS EXPERIMENT
By the year 1971 the new cesium-beam 'atomic' clock (our modern international standard of time) had been sufficiently developed to be called 'portable', to the extent that it could maintain an intrinsic accuracy of a few nanoseconds per day in the environment of a jet airliner. Accordingly, J.C. Hafele of the Washington University at St Louis, Missouri and Richard E. Keating of the US Naval Observatory in Washington, DC co-operated in an experiments designed to measure the timekeeping performance of travelling clocks, in a direct observation of Einstein's "dilation of time". A standard mean time was maintained on the ground at the observatory; four cesium clocks circumnavigated the world, first to the eastward and then to the westward.
Having allowed for times spent on the ground, for courses and speeds actually flown, and for the effects of the change of the gravitational potential with altitude (in accord with the general relativity theory), the experimenters calculated that the westbound clocks should show a net gain of time, relative to the "fixed" time standard in Washington, of about 250 to 300 ns over the whole trip. By contrast, due to the approximate balancing of the two effects (motion and gravitation), the eastbound clocks should just about break even on completion.
That was their theoretical prediction and, within the accuracy of their estimations of flight path, it was what they actually observed.
In the face of what seemed to them a magnificently clear-cut demonstration of the correctness of both of the relativity theories, it was difficult for the relativists to understand why the Hafele-Keating result did not immediately convince all scientists once-and-for-all of the truth of the relatively concept.
But between the skepticism of the physicists on the one hand and the condescension of the mathematicians on the other, conditions for even discussing such difficult ideas have always been far from ideal.
The dissent of the non-relativists in this case might perhaps be put into words as follows: According to Einstein's special theory the Principle of Relativity is paramount; that is, every observer in uniform motion is equally entitled to declare that his own local environmental system is at rest. In what way, then, do the clocks at the US Naval Observatory differ from those in the aircraft? If the westbound aircraft is moving westward at velocity v relative to the observatory, then so also is the observatory moving eastward at velocity v relative to that aircraft. Surely this must mean that each clock must run more slowly than the other--the well-known paradox? What you have declared in your calculations is that because of the rotation of the earth your eastbound clock is travelling fastest, at velocity (lr + u, the Naval Observatory is slower, at velocity v = Or, and the' westbound clock is slower still, at velocity fir --u. * From this you claim to deduce, by Einstein's theories, that the eastbound clock will run slower than the observatory clock, while the westbound clock will run faster. But measured relative to the observatory the aircraft's speeds are the same, so that the proportional slowing of their clocks should also be the same, namely delta_t/t =-1/2 u^2/c^2: differential time loss is zero.
By assigning different absolute speeds to the two aircraft, as you have done, you have allowed one particular reference frame (that is, the frame which is at rest relative to the geo-centre) to be preferred for this purpose over, for example, that of the Naval Observatory. If your experimental result agrees with your assumption of the existence of this preferred standard of rest--and it seems that it has done so--then it must deny Einstein's first postulate, the Principle of Relativity.
Far from demonstrating support for Einstein's theory therefore, as you intended it should, your experiment has in fact served to disprove its premise and hence the theory itself.
The experimenters had foreseen that particular criticism, and had taken care to forestall it by inserting the following sentences into their experimental report:
"Because the earth rotates, standard clocks distributed at rest on the surface are not suitable in this case as candidates for coordinate clocks of an inertial space. Nevertheless, the relative timekeeping behavior of terrestrial clocks can be evaluated by reference to hypothetical coordinate clocks of an underlying nonrotating (inertial) space."
-and again, as a footnote:
"It is important to emphasize that special relativity purports to describe certain physical phenomena only relative to (or from the point of view of) inertial reference systems, and the speed of a clock relative to one of these systems determines its timekeeping behaviors (G. Builder, 1958)."
Although couched in esoteric, 'relativistic' jargon, what is being said here is extremely important because it proposes a re-interpretation of one aspect of special relativity which it suggests has been universally misunderstood. Paraphrased, it says that an observer must be "at rest relative to an inertial frame of reference" (i.e. un-accelerated himself) if the explanations of the physical observations are to be meaningful; but not such restriction applies to the phenomenon being observed--which might legitimately be an electron orbiting inside a hydrogen atom at about 10^15 revolutions per second, or a muon travelling at over 99% of the speed of light and under enormous centripetal acceleration in a storage ring at CERN,' or a clock airborne in a Boeing 707.
And there is no need for any second "observer" to be involved: this Relativity is not reciprocal.
[[*Omega is earth's angular velocity, r is earth's radius, and u is speed of the aircraft over the earth's surface, assumed to be along the equator in this example: Omega = 465.1 m/s u 220 m/s.]]
By these criteria the relativistic equations (the Lorentz transformations) do not require that there should be any symmetry between an observer's laboratory clock and the clocks of the muons that he may be examining. Reciprocity of time-keeping is to apply only between observers both of whom are moving inertially, and one of the three observers in Hafele and Keating's experiment was truly inertial. It seems to be inertial motion, not relative motion, that is now important. It is easily shown by this argument that any other ‘inertial observer'--one situated above the north pole, say moving axially away from the earth at a constant, inertial velocity--will observe exactly the same time differences between the experimental clocks as would an observer who was "stationary" at the pole itself or, hypothetically, at the geo-center. But an earthbound observer, it seems, will see something different.
In summary, any technician who tries to compare the rates of clocks at the US Naval Observatory, Washington, DC with others at the Royal Greewich Observatory, Herstmonceux, or for that matter at the National Physical Laboratory in Teddington, is going to get a wrong answer.
-------- HAFELE-KEATING-BUILDER RULES OF RELATIVITY -----
-- Estimates and observations of the behavior of time as measured by clocks are valid only when referred to some real or hypothetical inertial (un-accelerated) frame of reference.
Clock readings estimated or observed from different inertial reference frames will differ as between each other, but all will be equally valid ('relativity of simultaneity'). C) If v is the velocity of any clock relative to any inertial reference frame K, then the rate of that clock as observed from K will be et=-1/2v2/c2.
-- The rate of any clock depends directly upon the gravitational potential at the location of the clock.
011 V is the difference between the gravitational potentials at the locations of any clock and any reference point Q. then the rate of that clock as observed from Q will be t/t= O No restriction of any kind is placed on the motion of the clock whose behavior is being observed; and in particular the acceleration of an ideal clock, whether caused by gravitational or local mechanical forces, has no effect on its timekeeping behavior.
The effects of relative velocity (v) and relative gravitational potential (V) on timekeeping are simply additive. If either or both of V and v should vary during the observing period their overall effects on timekeeping are to be obtained by integration.
---------------
FURTHER DISCUSSION: SOME CONSEQUENCES
The Hafele-Keating-Builder argument provides an answer to Dingle's 1967 questions, which until now has gone unanswered.
Dingle had quoted Einstein's statement (at the head of this article) and asked: "What entitled Einstein to conclude from his /special relativity] theory that the equatorial, and not the polar, clock worked the more slowly?" The answer, it now seems, is that it is only the 'fixed' (inertial) observer--at the pole--who is entitled to hold a valid opinion about the physical fact of the relative rates of the clocks. Any observer whose state is not ‘inertial' within a necessary degree of precision must automatically come to some erroneous conclusion. It would seem that the earlier argument, that the rotating earth is not an "inertial reference system" within the restrictions of the special relativity theory, was correct.
At the same time it is worth noting that the clock-slowing effect due to motion which was observed in this experiment, assumed genuine (and most certainly it needs to be confirmed by repetition), is according to this explanation entirely due to the special or restricted relativity theory; Einstein's general relativity theory is involved here only as a necessary correction to allow for the variation of the earth's gravitational potential with altitude. This is a static effect-a point which will become important later on. And, remarkably, nowhere has there been a mention of acceleration.
This new interpretation of relativity is completely at variance with previous attempts to resolve the twins paradox (the asymmetrical-ageing variant of the clock paradox, during a space journey). The standard explanation, for example by Sir Hermann Bondi, supposes that some unspecified effect of acceleration modifies the behavior of one of the clocks; it fails through its vague inability to handle more than one case without changing the assumption.
Even the explanation due to Einstein himself, which is specific enough but which relies on a abstruse and unconvincing ad hoc argument (devised for a different purpose anyway), permits an accelerated observer to draw correct deductions about a distant clock. Nor is this the only difficulty that arises if one follows this route: for the paper by Builder, on which Hafele and Keating chose to rely, was in fact arguing the case for a Very Special theory of relativity of Builder's own, in which he claimed, "Thus we conclude that the relative retardation of clocks predicted by the restricted theory does indeed compel us to recognize the causal significance of absolute velocities." (My italics). So clearly we are no longer dealing with Einstein's theory of relativity; there seems to be little left of that but the name! Nevertheless, the new interpretation (or theory) is self-consistent, has provided an answer to Dingle's Question, seems to have resolved the twins paradox, and incidentally seems to agree with experience--that is, the Hafele-Keating experimental results are consistent with the Builder interpretation--so that one has no choice but to take it seriously. Not least of its virtues is that, despite Dingle's protest, it supports Einstein's polar-vs-equatorial clock contention word for word.
EXPERIMENTAL TEST OF EINSTEIN'S STATEMENT
But we have not reached the end of the matter. Is it really true that a clock on the equator will run more slowly than a clock at one of the earth's poles, as Einstein originally suggested?* This is an issue that could be put to practical test. Hafele and Keating by their experiment have alerted us to the accuracy to be expected of modern atomic clocks. The amount of the differential timekeeping discrepancy between polar and equatorial clocks, according to all interpretations of special relativity, is not in doubt: given the earth's equatorial velocity v =Omega= 465.08 m/s, it is
delta_t/t= --1/2v^2/c^2 =-1.2033 x 1042
or A t=-104.0ns per day.
A discrepancy of this magnitude is well within the measurement capability of installed (non-portable) cesium clocks, and to make matters easier still, the rate is constant and cumulative over an observing period of unlimited duration. Thus neither the intrinsic accuracy of the clocks nor their readability is a determining factor in the feasibility of this experiment.
Various difficulties present in the Hafele-Keating experiment are not relevant here.
For example, two sources of error were the integrated geographic locations of the clocks, then carried in aircraft but now fixed, and their velocities over the surface, now zero. There, gravitational effects of altitude varied from zero at sea level to delta_t = +113ns per day at the 12km operating altitude of the 707. Here, the south pole is the obvious choice, since it lies on a land mass and it is the site of a permanent international scientific base. Its height is some 3,000 meters above sea level; if the modern city of Quito (altitude 2,850m) were selected as the corresponding equatorial site, the timing discrepancy due to altitude (gravitational potential, from the general relativity theory) would also be reduced to insignificance. We would then be testing the time dilation of special relativity alone, directly, and without confusing side-issues.
The only technical problem remaining in this experiment is the obvious one--how does one compare the readings of the polar and equatorial clocks in situ? The well-tried method is to rely on radio signals for the transmission of timing information between them. Provided the comparison is mutual (that is, by simultaneous two-way links), such communications links are self-compensating: slow phase drifts in both directions over the same transmission path will cancel each other out to second order.
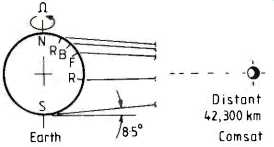
Synchronous or geostationary communication satellites, whose residual station-keeping errors are limited to just a few kilometers and whose relative motions are smooth and very accurately repetitive over the sidereal day, are entirely suitable for this task. (It will be remembered that we are interested in the differential rates of these clocks, not their synchronization, so the mean length of the link is immaterial). However, for our purpose the Satcom link suffers from the prohibitive snag that geostationary satellites are necessarily positioned some 8 1/2 degrees below the local horizon as seen from the pole itself (Fig. 2), so that the timing waveforms would have to Einstein's text (at the head of this article) is the statement that clock B runs slower than clock A while clock A runs faster than clock B, and as such it involves no "paradox". be relayed over about 1,000 km by tropospheric scatter or short-wave ionospheric link before being transmitted out to the satellite. Such links are notoriously prone to n Distant 42,300 km Earth B'5° Comsat multipath interference effects: the result would be to destroy the vital self-compensatory properties of the two-way links. So for the time being we cannot work to and from the poles themselves.
But all is not quite lost. Probably the highest latitude for a terminal with en clair access to a synchronous satellite-while also incidentally looking under the auroral multipath zone--is about 70°. Iceland is an obvious candidate. A clock in the observatory at Reykjavik, at 64° north and at sea level, could with great convenience be compared by direct satellite link with a similar clock at Recife, Brazil, at 7° south and also at sea level. As promising sites to complete an experimental network one might suggest Brighton (51°N) on the UK coast near Herstmonceux, and Funchal (32°N) in Madeira. The predicted relative time dilations at these stations are readily calculable: between Reykjavik and Recife the slip-rate should be-82.5 ns per day, and even over the short Sussex-Madeira link it should still be-33.6 ns/day--that is, a discrepancy of one complete cycle per day at 30MHz.
We do not need to perform this experiment today because its result is known already. International time centers have been comparing the rates of each others' standard clocks for many years as a matter of routine. The finding is that relativistic differential time dilation as predicted by Einstein and implied by Hafele and Keating does not in fact take place. No mention of it appears in the CCIR Report which deals with the presumed effects of relativity on international timekeeping. If this result puzzles you, you have my sympathy; please read on.
A WHIFF OF PARADOX...
Let me amplify that a little, and try to make it clearer. Hafele and Keating's formula for the proportional timekeeping behavior of their airborne clocks, or time dilation, was
delta_t/ = gh/c^2 --1/2V^2/c^2. (1)
The term -1/2v^2/c^2 is Einstein's 1905 prediction due to motion at velocity v (by special relativity theory), where
v = Omega r cos phi+ u, (2)
Phi being the latitude and u being, effectively, the eastward component of the aircraft's speed over the earth's surface. The term +gh/c^2 is an extra, static contribution from general relativity theory, due to the earth's gravitational field; if g is the acceleration, then gh represents the gravitational potential, relative to the earth's surface, of an airborne clock at altitude h. It is held by the Relativists that the Hafele-Keating results, which are said to be entirely consistent with equation 1, provide via its term gh/c^2 and 1/2v^2/c^2 a complete and satisfactory confirmation of both the general and the special relativity theories.
That would be a magnificent outcome if it were true, but unfortunately it suffers from the following small difficulty. Rather than flying these aircraft, keep them on the ground for a day or so. Then their altitude above sea level becomes permanently h = 0 and their ground-speed remains permanently u=0. Making those simplifying substitutions in (1)--which must of course apply just as well to clocks in grounded aircraft--the time-dilation prediction becomes:
delta t/t =-1/2v^2/c^2=1/2( Omega r 4))^2/c^2, (3)
where v = Omega cos phi is simply the eastward motion due to earth rotation (only) of the grounded aircraft at latitude .. And it must describe equally well the eastward velocity of the US Naval Observatory at its latitude, or the Reykjavik and Recife Observatories at their respective latitudes.
Clearly, by this relativistic formula the local dilation of time, delta t/t, should be proportional to the simple function (cos^2 phi)) of an observatory's latitude, as predicted by Einstein and in agreement with the Hafele Keating experimental result. But the truth is that the timekeeping of fixed (earthbound) observatories at sea level does not demonstrate a systematic dependence on latitude.
Surely somebody should have asked, Why not?
...AND A RELATIVISTIC WRIGGLE
This failure of fundamental theory, which from the point of view of the philosophy of science might be considered quite an important failure, was relegated by Hafele and Keating to a mere footnote in their report, in which they cited a discussion by W.J. Cocke:
"Clocks at rest on the earth's surface (at average sea level) keep the same relativistic time independently of latitude differences. The effect of the difference in surface speed at different latitudes is cancelled to lowest order by a corresponding effect from the difference in surface potential owing to the oblate figure of the earth.”
Although just what the `relativistic time' means in this context is not clear, we can still analyze this argument. As defined above, (gh) was the gravitational potential, relative to sea level, due to flight at altitude h. Here it would seem that another kind of 'h' --H, say actually the height difference between the earth's local radius r at latitude 4, and its polar radius b, due to oblateness--is to be made responsible for cancelling out the two relativistic effects of velocity (Special theory) and gravitational potential (General theory) exactly, in accord with the very convenient equation
gH/c^2-1/2v^2/c^2 = 0! (4)
The elegant simplicity of this proposal may well serve, for believers, to conceal the fact that it is untenable. The reason why the earth's surface follows its flattened, oblate (elliptically curved) shape is simply that everywhere on its surface, neglecting effects gravity (plumb-line) is at right angles to the local horizontal (spirit-level); if it were not, the oceans would flow north or south to make it so. The fallacy in the argument lies in assuming that the gravitational term Vg=(GM/r2)H=gH represents the whole of the matter; but the centrifugal term V. (the cause of the earth's oblateness) must also be included. When it is, (see panel), the total gravitational potential at each observatory clock is not just Vg=gH as in equation 4, but exactly Vg+Vc=0. Pace W.J. Cocke, the surface of the geoid--mean sea level, where h=0 --is now (and always has been) a uni-potential surface world-wide.
In other words, the gravitational potential at sea level is the same everywhere in the world. Hafele and Keating's "difference in surface potential owing to the oblate figure of the earth" does not exist. It follows that general relativity is irrelevant to this argument, since its contribution is zero; it does not influence the timekeeping of clocks at sea level at different latitudes, however desirable such an influence might have been for the defense of relativity theory.
INTERIM CONCLUSION
"To sum up: In 1905 Albert Einstein predicted, as a consequence of relativity theory, free of paradox, that an ideal clock [at sea level] on the equator would run more slowly than an identical clock [also at sea level] at the earth's pole. An experiment performed in 1971 purported to confirm the influence of both special and general relativistic effects on the timekeeping of quasi-ideal clocks.
The theory which was said to underlie that experiment was also seen to support Einstein's original prediction.
"However, it is observed that the differential slowing of clocks due to latitude alone (independent of geographic motion and altitude), which was predicted by Einstein, does not in fact take place. It seems that the explanation put forward --and apparently generally accepted --to account for this theoretical failure was physically unsound."
References
1. Einstein, A. On the Electrodynamics of Moving Bodies; trans. in The Principle of Relativity.
Methuen, 1923 and Dover, 1952. pp.49-50.
2. Dingle, H. Science at the Crossroads, Martin Brian and O'Keeffe, 1972. p.40ff.
3. Essen, L. Einstein's Special Theory of Relativity, Proc. Royal Institution, vol 45, 1972, p141: p.150ff.
4. Hafele, J.C. and Keating, R.E. Around-the --world atomic clocks (two papers), Science, vol.
177, 1972. pp.166,168.
5. Hafele & Keating, Op.cit. (4): p.166 col.2 & p.167n(6).
6. Builder, G. Ether and relativity, Aust. J. Phys. vol.11,1958 p.279.
7. Farley, F.J.M. & Picasso, E. The muon (g-2) experiments, Ann.Rev.Nucl.Part.Sci. vol.29, 1979 p.243: pp.259,266.
8. Dingle, H. Op.cit.(2): pp.45-46.
9. Bondi, H. Assumption and Myth in Physical Theory. Cambridge, 1967. pp.43-52.
10. Einstein, A. Dialogue concerning objections to Relativity Theory", Naturwiss. vol.48. 1918p.697; German, untrans. (Part translated in Dingle, Op.cit.(2): pp191-195).
11. Builder, G. Op.cit.(6): p.282.
12. Relativistic Effects in a Terrestrial Coordinate Time System CCIR Report No. 439-3, 1982.
(Defines TAI). 13. Cocke, W.J. Relativistic corrections for terrestrial clock synchronization; Phys.Rev.Lett. vol.16, 1966 p.662.
14. Hafele & Keating, Op.cit.(4): p.168n (9).
15. 'Measured' numerical values inserted into eqn 4 will not yield the result Vg + V. = 0, because the earth is neither spherical nor of uniform density and one has to deal with small differences between very large quantities; for example, the observed value of "g" at the poles is 9.8321 m/s2 whereas the calculated value from GM/b2 is 9.8660 m/s2, a discrepancy exceeding 0.3%. It is as though the apparent position of the geo-center varied by up to 11km, depending on the observer's latitude. The direction of the local vertical is subject to a similar small discrepancy (5.4' arc at latitude 45°) for the same reasons. The precise statement is that the geoid is defined as a unipotential surface in earth coordinates--if one understands potential in its usual, field-theory sense.
Dr Scott Murray's biography appeared in the June 1983 issue.
------------------

Fig. 3. The vector accelerations acting on any particle or body at sea level
and geocentric latitude 4, are two:
which by definition is zero over the entire geoid surface. Thus the contribution of general relativity to timekeeping at sea level is nil.
Note particularly that the term-1/zv2 in (C) is derived from the gravitational potential (general relativity), and is not to be identified with the term --1/2v^2/c^2 of equation 1 in the main text, which was derived from the Lorentz transformations (of the special relativity theory).
==========
(adapted from: Wireless World , Dec. 1986)