by ROY ALLISON
[Roy Allison, founder of Allison Acoustics, joined with Edgar Villchur and others to form RDL Acoustics, in Bellingham, Mass., in 1992.]
Anyone who is familiar with my work knows that I've spent a lot of time on the problem of the ways speakers interact with room boundaries (walls, ceiling, floor) and how this affects sound. This work has led my current company, RDL Acoustics, to develop a simple, inexpensive ($5!) program, Bestplace, for Windows or Macintosh computers; it can tell you a great deal about how your speakers will interact with your listening room.
Bestplace can tell you just where to place your speakers in your room to achieve the optimal interaction with room boundaries.
You only need to enter three simple measurements; the rest is pretty much a matter of clicking on an on-screen "button" or pressing your computer's "Enter" key.
Let's look briefly at why and how the interaction between speakers and room boundaries occurs. The movement of the cone in a direct-radiator loudspeaker is determined almost completely by its own internal construction and its enclosure, not by any external forces. However, the sound power the cone motion produces is very much dependent on the cone's acoustic load-the radiation resistance, specifically.
Throughout the lower half of the audible frequency range, nearly five octaves, a loudspeaker's ability to radiate sound power is sensitive to its nearby environment. There fore, its power response is affected by its location in a room. The changes in response with location can be large, both additions to and subtractions from the loudspeaker's free-space power output. The variations with location are not intuitively obvious; they are calculable, but the math is quite tedious to perform without the aid of a computer. That is why we have developed Bestplace, a computer pro gram to calculate and plot a room's augmentation to a speaker's anechoic power response. The only data you must enter in the program are the distances from the center of the woofer cone to the three nearest room boundaries. These numbers determine how the speaker's output will be changed by its environment.
=============
The Waterhouse Equation
Waterhouse developed an expression for the ratio of power radiated by a small sound source, located near three mutually perpendicular room surfaces, relative to the power that would be radiated by that same source in free space that is, with no boundaries nearby.
("Small" in this context means small in comparison with the wavelength of the frequency radiated. The usual direct-radiator woofer becomes progressively "smaller" as the frequency de creases below about 500 Hz.) This ratio may be either a positive or negative number and is the sum of eight parts. The first part is the original free-space power, which is augmented (or diminished) by the sum of seven reflected impedances: Three from the individual boundary surfaces, another three from the two-boundary intersections, and a seventh one from the three-boundary intersection. The maximum possible output occurs when the source is at zero distance from the corner, in which case Waterhouse's formula has a value of 1 for each term. The total is then 8, for a gain of 9 dB. Of course. zero distance is not possible in the real world, and the gain drops rapidly as the distance between the source and the corner increases.
=============
Theory
Suspended centrally, equidistant from opposite pairs of boundaries in a room, a loudspeaker system's power response is, for practical purposes, the same as it would be in an anechoic chamber. If it is moved down so that the woofer is very close to the center of the floor, low-frequency power output increases 3 dB because the reflected pressure, in phase with the direct output from the cone, doubles the radiation resistance.
Moving the speaker again, so that the woofer is brought very close to the intersection of the floor and one wall, doubles the radiation resistance again, with another 3-dB increase in power output. If we next move the woofer very close to a three-boundary intersection--i.e., the floor and two walls-we would once again in crease the output by 3 dB. Not bad: An eightfold increase in efficiency just by changing the location of the speaker! But wait. You knew there had to be a catch, in this case means at a very small fraction of a wavelength. This is easy to manage at low frequencies but rapidly gets more difficult as the frequency rises and the wavelength be comes shorter. The formula for wavelength (in inches) is 13,560 divided by the frequency; a 10th of a 30-Hz wavelength is 45 inches, but a 10th of a 300-Hz wavelength is only 4 1/2 inches. It wouldn't be easy to de sign an enclosure that would put the center of a 10-inch woofer just 4 1/2 inches from each of three intersecting room boundaries. It is interesting to see the changing effects of boundary reflections on speaker output as the reproduced frequency rises.
Waterhouse [1, 2] and Waterhouse and Cook [3] investigated the matter quantitatively, developing the formula described in the sidebar "The Waterhouse Equation." I confirmed their findings experimentally [4, 5] as they apply to loudspeakers in listening room environments, and pointed out the design consequences. Ballagh [6] and Adams [7] have also made significant contributions.
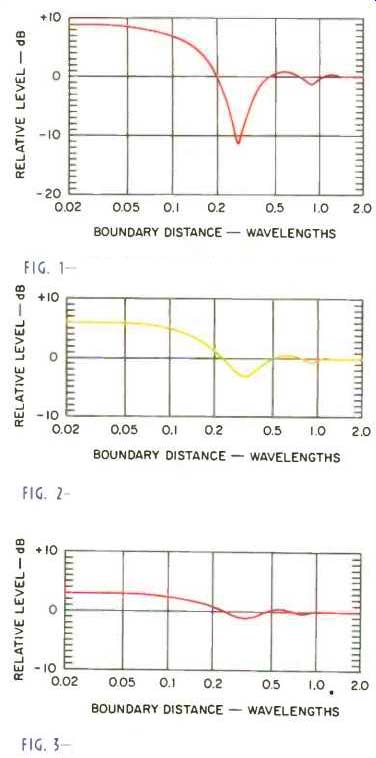
FIG 1--augmentation of three room boundaries when the speaker is equidistant
from all three nearby intersecting boundaries.
FIG. 2--augmentation of two equidistant intersecting boundaries. With third boundary removed.
FIG. 3--augmentation of a single near by room boundary: other boundaries are far away
Figure 1 shows what happens when the three boundaries. At 0.1 wavelength, the power response has fallen nearly 2 dB from its maximum of 9 dB; at 0.2 wave length, it reaches 0 dB, the free-space value, and at 0.28 wavelength, it has plum meted to 11.3 dB below its anechoic value! The power response then rises and ripples a dB or so above and below 0-dB augmentation. For perspective: If the woofer is 24 inches from each boundary, this distance is 0.1 wavelength of 56.5 Hz, 0.2 wave length of 113 Hz, and 0.28 wavelength of the notch frequency, 160 Hz. The notch is created because the strong reflections combine at the woofer cone's surface in phase opposition to the direct output, reducing the radiation resistance at that frequency far below its free-space value. Above 0.5 wavelength (282 Hz in our example), the perturbations are minor.
Figure 1 shows the worst-case condition-fortunately. Suppose we have a large distance from one boundary, effectively putting the woofer equidistant to only two intersecting boundaries. The resulting augmentation curve then looks like that in Fig. 2, where the maximum gain is 6 dB but the notch depth is reduced to 3 dB.
Carrying the process one step further, by having only one nearby boundary, produces the curve in Fig. 3, which shows 3 dB maximum gain and only a 1-dB notch. There is a linear increase of 3 dB each time we bring the woofer close to another boundary but a decidedly nonlinear in crease in the notch depth.
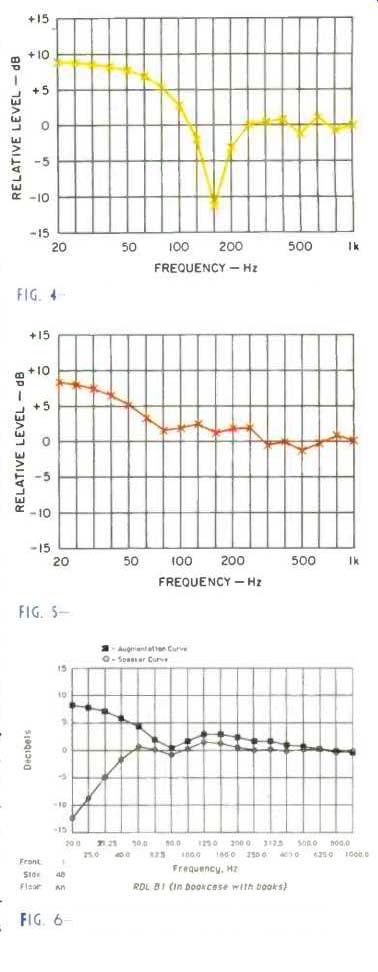
Fig. 4--Augmentation. In third octaves. For a woofer 24 inches away from
each of three mutually intersecting boundaries: plot has been redrawn from
Bestplace output.
Fig. 5--Augmentation. In third octaves. For a woofer spaced 10. 36. And 60 inches from nearest room boundaries: Plot has been redrawn from Bestplace output.
Fig. 6--Bestplace printout. Macintosh version. For RDL acoustics bookshelf speaker surrounded by books.
SMOOTHING THE AUGMINTATION CURVE
The problem of uneven augmentation would obviously be minimized if we could neutralize one room boundary. There are a few ways this can be done. One way is to mount the speakers in the wall, flush with its surface. Another way, feasible with true bookshelf-size speakers, is to place them in bookshelves surrounded by books. A third way, possible only in very large rooms, is to place them far from a third boundary. This would have to be at least 12 feet from one wall in order to limit the boundary's effect to below 50 Hz.
For one reason or another, none of these options is available to most of us. We must deal with three room surfaces close enough to our speakers to influence their behavior. We can make that influence a good one, or at least a fairly neutral one, by taking advantage of the fact that the notch from a single boundary is mild.
This can be done by making the woofer's distances to the three nearest boundaries as different as is practical, so that-rather than suffering the single crevasse in power output when all the distances are nearly the same there are several much smaller dips and a smoother curve overall.
In most loudspeaker systems of medium to large size, the woofer is located not far from the center of the front panel, which limits the maxi mum value attainable for the distance ratio. If the woofer is on the top panel (or, in a floor-standing system, close to the bottom of the front or side panel), the minimum distance between the center of the woofer and one room surface can be as little as 6 or 7 inches.
(Three of the four mid-size speakers I've recently designed are like this; the other is a bookshelf model.) Even with this advantage, however, performance should be optimized by evaluating the impact of the other room boundaries.
The Bestplace program (based on the Waterhouse formula) was developed to aid in this process, by allowing you to see in advance the effect of pos Bible changes in speaker location. The program plots, in addition to the room augmentation curve for the distances entered, a power output curve for my company's speakers in that location. However, it is made more generally useful by a "Not an RDL speaker" option in the curve menu; only the augmentation curve is plotted with this selection. Figure 4 is a Bestplace augmentation curve corresponding to the curve in Fig. 1, obtained when 24 inches is entered for each of the three boundary distances. In Fig. 5, the distances are 10, 36, and 60 inches, yielding a much smoother curve.
If you know the anechoic power output of your speaker (not the on-axis anechoic frequency response), you can add it to the augmentation curve Bestplace gives you to obtain your speaker's power output in that location. Note that a near-field woofer measurement is not the same as a full-space (or anechoic) total power measurement, on which the Water house formula is based. To convert a near-field measurement to a rough equivalent of full-space power, you must subtract 3 dB below the frequency at which the cabinet's front panel becomes a half-space baffle.
The region of the transition frequency depends on the size of the baffle, but if you gradually phase in the change in level from 300 to 600 Hz, you probably won't be grossly off. As a corollary, if you are making calculations based on flush-mounting your speaker, you can use a near-field woofer measurement directly and not have to make the conversion. Flush mounting (or bookshelf mounting with surrounding books) is essentially a half-space environment to start with, which is what a near-field measurement simulates.
=============
Using the Program
When Bestplace is loaded in Windows, the welcome screen offers two choices. One button generates a help menu; the other, labeled "OK," clears the screen except for a three-choice menu bar at the top. These choices are "File," "Run Program," and "Help." "Help" brings down the same menu as can be accessed from the welcome screen.
"Run Program" drops a single-item menu labeled "Create graph." Pressing that button brings up a screen headed "Input Graph Parameters." The first selection, "Select a speaker type," scrolls a list of RDL Acoustics models and then the choice of "Not an RDL speaker," the general-use se lection. Following the window for speaker choice is one with boxes for entering distances from the center of the woofer to the three closest room boundaries. Once these are entered, you are offered a choice of "Cancel" or "Graph" buttons to press. If you choose "Graph," a graph of boundary augmentation versus frequency will be displayed, based on the distances you have entered. If you selected an RDL model to investigate, its power output in that location will also be shown. (Figure 6 shows such a graph, from the Macintosh version of the program.) When the graph has been plotted, you can plot a new one for a different combination of distances by clicking on the "Run Program" menu again. The menu bar re mains on screen with the graph. You may also press "Help." Or, if you press "File," a drop-down menu offers three choices: "Copy to Clipboard," "Print; or "Exit." Bestplace is available on diskette in both IBM and Macintosh versions; in the case of IBM, on either 3 1/2- or 5 3/8-inch diskette. The cost is a nominal $5, postage included.
You may place an order by writing to RDL Acoustics ( 26 Pearl St., No. 15, Bellingham, Mass. 02019) or, if you want to use a credit card, by phone (800-227-0390). Be sure to specify which version you want. Both versions of the program can be downloaded free of charge from the RDL Bulletin Board (800-227-0391). If you'd like technical papers on room boundary effects, including the Waterhouse formulas and verification measurements, they are available free of charge from the same source.
REFS.
1. Waterhouse, R. V., "Interference Patterns in Reverberant Sound Fields," Journal of the Acoustical Society of America, Vol. 27, No. 2 (March 1955).
2. Waterhouse, R. V., "Output of a Sound Source in a Reverberation Chamber and Other Reflecting Environments, "JASA, Vol. 30, No. 1 (January 1958).
3. Waterhouse, R. V. and R. K. Cook, "Interference Patterns in Reverberant Sound Fields, II," JASA, Vol. 37, No. 3 (March 1965).
4. Allison, R. F., "The Influence of Room Boundaries on Loudspeaker Power Output," Journal of the Audio Engineering Society, Vol. 22, No. 5 (June 1974).
5. Allison, R. F., "The Sound Field in Home Listening Rooms, II," JAES, Vol. 24, No. 1 (January/February 1976).
6. Ballagh, K. O., "Optimum Loud speaker Placement Near Reflecting Planes," JAES, Vol. 31, No. 12 (December 1983).
7. Adams, G., "Time Dependence of Loudspeaker Power Output in Small Rooms," JAES, Vol. 37, No. 4 (April 1989).
(Adapted from Audio magazine, Aug. 1994)
Also see:
Coloration of Room Sound by Reflections (Mar. 1993)
Bass vs. Space: Room Acoustics and Good Sound (Audio magazine, July/Aug. 1999)
Flying Blind--The case against long-term listening (March 1997)