by J. ROBERT STUART
[J. Robert Stuart is chairman and technical director of Meridian audio and chairman of the acoustic renaissance for audio. An organization founded to campaign for establishment of a dvd-audio standard that would assure the highest possible quality of sound reproduction.]

Sound, starts as a vibration in air, and we perceive it through a hearing mechanism that is not exclusively analog in operation.
But since, at any sensible scale, the vibration can be considered an analog signal, there has been considerable debate over why what is and ends as an analog air-pressure should be stored digitally. The overwhelming reason to store and transmit information digitally is that it can be conveyed without loss or the introduction of interference. It can even (as we will see later) br manipulated in a way that avoids many of the distortions introduced by analog processing. This somewhat obvious point is of ten overlooked. Analog storage or transmission methods always introduce distortion and noise that cannot be removed and also threaten the time structure of the sounds through wow or flutter effects.
Digital audio has progressed on this basis, and on the assumption that we can convert transparently from analog to digital and back again. A number of experiments have demonstrated this possibility to varying degrees, but it has also become fairly well understood that badly executed digital audio can introduce distinctive problems of its own.
The Compact Disc was the first carrier to really bring digital audio into the home, and its development has taught us a lot. But as digital audio has progressed, we have evolved the capability to record and play back with resolution exceeding that of the standard Red Book CD-two channels of 16-bit linear PCM audio sampled at 44.1 kHz-and current studio practice recognizes this Red Book channel as a bottle neck. High -quality recordings are routinely made and edited using equipment whose performance potential is considerably higher than that of CD.
Along the way, some interesting ideas have been proposed to try to maximize the potential of CD with respect to the capabilities of the human auditory system. One is noise shaping. This technique was first pro posed by Michael Gerzon and Peter Craven in 1989 and has been successfully embodied in Meridian's 618 and 518 processors, Sony's Super Bit Mapping (SBM) system, and elsewhere. Noise shaping has been used on maybe a few thousand titles, but these include some of the very finest-sounding CDs available today. Other proposals were interesting but didn't get off the ground: subtractive dither, for example, and schemes to add bandwidth or channels to CDs.
I have felt strongly for some time that we are on the threshold of the most fantastic opportunity in audio. It comes from two directions. First, psychoacoustic theory and audio engineering may have progressed to the point where we know how to define a recording system that can be truly transparent as far as the human listener is concerned. Second, we will soon see the evolution of a high -density audio format, related to DVD, that will have, if it is used wisely, the data capacity to achieve the transparency we seek.
THE MEASURE OF THE MEDIUM
I am firmly convinced that this next-generation audio distribution format should be capable of delivering every sound to which a human can respond. Achieving that re quires: sufficient linearity (i.e., low enough distortion), sufficient dynamic range (i.e., low enough noise), sufficient frequency range, sufficient channels to convey three dimensional sound, and sufficient temporal accuracy (wow, flutter, jitter).
The Acoustic Renaissance for Audio (ARA) has suggested that a carrier intended to convey everything humans can hear re quires: dimensionality (full spherical reproduction, including height), a frequency range from DC to 26 kHz in air (the in -air qualification matters), and a dynamic range from below the audibility threshold to 120 dB SPL.
Before delving deeper into these questions, we need to make a small diversion.
DIGITAL AUDIO GATEWAYS
Even among audio engineers, there has been considerable misunderstanding about digital audio, about the sampling theory, and about how PCM works at the functional level. Some of these misunderstandings persist even today. Topping the list of erroneous assertions are: (1) PCM cannot resolve detail smaller than the LSB (least-significant bit), and (2) PCM cannot resolve time to less than the sampling period.
Let's examine the first assertion. What is suggested is that because (for example) a 16 -bit system defines 64k (65,536) steps, the smallest signal that can be registered is 1/65,536, or about -96 dBFS. Loss of signals because they are smaller than the smallest step, or LSB, is a process known as truncation. Now, you can arrange for a PCM channel to truncate data below the LSB, but no engineer worth his salt has worked like that for more than 10 years. One of the great discoveries in PCM was that adding a small random noise (called dither) can pre vent truncation of signals below the LSB.
Even more important was the realization that there is a right sort of random noise to add and that when the right dither is used the resolution of the digital system becomes infinite. What results from a sensible quantization or digital operation, then, is not signal plus a highly correlated truncation distortion but the signal and a benign low level hiss. In practical terms, the resolution is limited by our own ability to detect sounds behind noise. Consequently, we have no problem measuring (or hearing) signals of -110 dBFS in a well-designed 16 -bit channel.
As regards temporal accuracy (assertion 2), if the signal is processed incorrectly (i.e., truncated), the time resolution is indeed limited to the sampling period divided by the number of quantization levels -34.6 picoseconds for CD audio. We are again saved, however, as application of the correct dither makes the temporal resolution effectively infinite as well.
So, we have established the core point, that wherever audio is quantized (as in an analog -to -digital converter) or requantized (as in a filter or other DSP process), there is a right way and a wrong way to do it. Neglect of the quantization effects will lead to highly audible distortion. However-and this is perhaps the most fundamental point of all-if the quantization is performed using the right dither, then the only consequence of the digitization is effectively the addition of a white, uncorrelated, benign, random noise floor. The level of the noise depends on the number of the bits in the channel, and that is that!
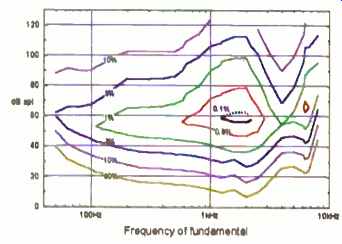
Fig. 1--Detectability contours for second-harmonic distortion. The SPL,
is of the fundamental frequency: inside a contour, distortion of the marked
percentage should be audible.
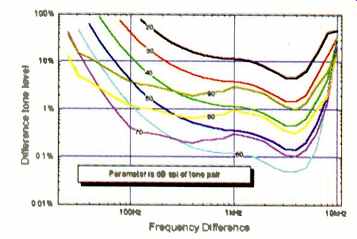
Fig. 2--Predicted detectability of a difference tone produced by IM distortion.
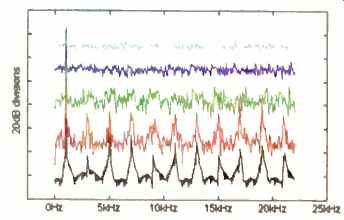
Fig. 3--FFT analyses of undithered 16 -bit quantization of a 1-khz tone
at -20, -10, -60, -80. and 90 dbFS. Curves offset by 25 dB.
LINEARITY
Linear, uniform PCM channels do not introduce distortion if suitable dither is applied at every stage where the audio is processed (i.e., modified rather than transmitted). It is possible to quantize and then process a signal without introducing any thing that we would commonly refer to or hear as a distortion.
But this is not to say that all digital systems are distortion -free, nor that all equipment has been correctly designed; had it been, there would be much less discussion about analog versus digital! The important point is that because it can be done perfectly, we should assume in designing a new carrier that it has been rather than make allowance for needless bad practice.
The reason for this preamble is that truncation-type distortions are of high order and so are far more likely to be audibly offensive than is a low level of uncorrelated random noise, which is a consequence of a good digital process and does not produce nonlinearity. In a well -designed, modern audio system, the significant nonlinearities (distortions) should arise only in the transducers and analog electronics, not in the PCM channel.
With that in mind, let us take one more short diversion, this time into the question of how much distortion we are able to hear.
It has been well established that the amount of distortion we can hear depends on its order--i.e., whether it is second harmonic, third harmonic, etc. And because the human hearing system itself is quite nonlinear, it also depends on how loud the main sound is.
Many of the examples in this article are evaluated using a computer model of auditory detection that I have developed over the years. This auditory model includes a step that calculates internal beats, or distortion products, in the hearing system. Figure 1 hints at the potential of such a tool. It shows a contour map estimating regions for detectability of pure second -harmonic distortion in mono presentation. The figure shows that at low loudness levels our ability to hear the added harmonic component is controlled by the absolute hearing thresh old. Maximum acuity occurs in the medium ground, corresponding to about 60 dB SPL. At this level, maximum acuity is estimated at around 1 to 2 kHz, where a 0.1% second -harmonic addition just reaches threshold. As sound pressure level increases, the broadening of the ear's cochlear filters and internal distortion reduce acuity.
Systems that introduce harmonic distortions also create intermodulation. Figure 2 illustrates the predicted detectability of intermodulation distortion, in this case of a first -order difference tone resulting from nonlinear processing. The horizontal axis is the frequency difference between one tone fixed at 10 kHz and an equal -amplitude tone at higher frequency. As with the harmonic example, we see that as the combination level is increased from 20 dB SPL, acuity rises rapidly, with maximum sensitivity again occurring around 60 dB SPL.
PRECISION AND DYNAMIC RANGE
Distortion can be introduced at analog-to-digital (A/D) or digital-to-analog (D/A) gateways or in analog peripherals. However, in a uniformly sampled, uniformly quantized digital channel, the bits maintain a precise 2:1 relationship. The potential for introducing distortion arises in nontrivial signal processing (including filtering and level changes) and in word -length truncation or rounding. But as we've noted, the nonlinear quantization distortion that results from truncation or rounding can be avoided completely by using appropriate dither in each nontrivial process.
Let us look at the distortion introduced by basic quantization more closely. Figure 3 shows level -dependent distortion produced in an undithered quantizer. The original signal, a 1-kHz sine wave, is attenuated in steps to show the effect of a fade on the out put of an undithered 16 -bit quantizer. At high signal levels, the quantization error is noise -like, whereas at low levels it is highly structured. It is hard to imagine that the structured distortion produced by truncation would not be audible.
On the other hand, dithered quantization introduces uncorrelated noise. Figure 4 shows FFT measurements of a -90 dBFS, 1-kHz signal subjected to 16-bit quantization with and without dither. In each case the signal appears at about the same level.
With dither, we see a smooth noise spectrum-the benign -sounding "error" introduced by correct quantization. Without dither, the signal is very rich in unwanted odd harmonics; the resulting total harmonic distortion (THD) is 27%.
Broadly speaking, truncated, rounded, and dithered quantizations introduce errors of similar total power but different composition. Through most of this article, I assume good practice and consider dynamic range and precision together. In a correctly engineered digital channel, the consequence of each quantization or requantization (word-length reduction or filtering, for example) is the successive addition of benign noise.
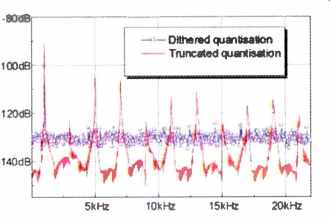
Fig. 4--FFT analyses of a -90dBFS. 1-khz tone quantized to 16 bits with
and without correct dither.
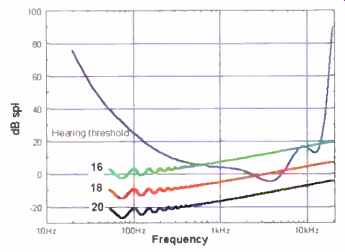
Fig. 5--Audible significance of the noise created by single, dithered
16- , 18- , and 20-bit quantizations, assuming a full-scale signal can
reach 120 db SPL.
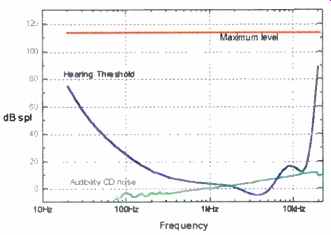
Fig. 6--Dynamic range of CD. The average human hearing threshold is included
for reference.
Figure 5 shows the base noise level for 44.1-kHz sampling in 16-, 18-, and 20 -bit channels. The noise is plotted, however, not in terms of spectral density (-137 dBFS/Hz with 16 bits) but in terms of audible significance to human listeners. The effect of the noise rises with frequency because of the effect of the filters in the human ear. The significance of the noise is plotted against an SPL reference that assumes the acoustic gain at replay will allow a full-scale digital signal to reach 120 dB SPL (a probable worst case). The average hearing threshold is also shown; wherever the noise curve is above the threshold, it may be audible. The magnitude and frequency range of the above -threshold spectrum indicates how it will sound. In the 16 -bit example, then, the component of noise between 700 Hz and 13 kHz should be audible in the absence of masking signals, whereas audibility is predicted between 2 and 6 kHz in the 18-bit example. This graph also suggests that for delivery, a 20 -bit channel should have adequate dynamic range.
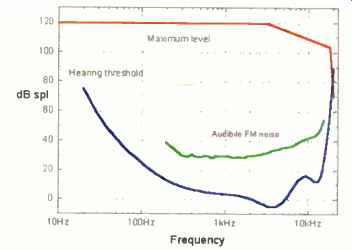
Fig. 7--Dynamic range of FM radio.
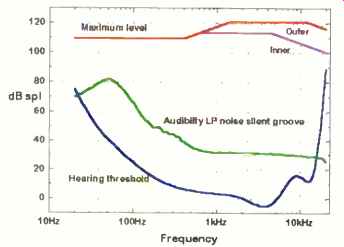
Fig. 8--Dynamic range of LP phonograph records. Maximum levels arc plotted
for both inner and outer grooves.
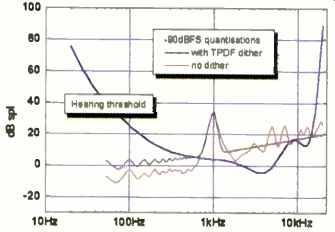
Fig. 9 --Audible significance of dithered and undithered 16-bit, 44.1
khz quantization of a 1-khz tone at -90dBFS (30 dB SPL, assuming 0 dBFS
equals 120 dB SPL).
DISTRIBUTION FORMATS
A distribution format, or carrier, is a means by which recorded music is conveyed to the public. Examples would include radio, TV, CD, and so forth. Normally a distribution channel has a limited (and fixed) rate of data delivery. But because the cost of computer data storage has been falling so fast, there is a temptation these days to regard data rates and quantity as relatively free goods.
Such a supposition might imply that the safest way to design a high -resolution re cording system or carrier is to use consider ably more data to represent the sound than prevailing psychoacoustic theory would suggest necessary. This is a dangerously naive approach, however, as it may lead to poor engineering decisions.
The quality of an audio chain reflects the degree to which it can maintain transparency. Any loss of quality will be due to an error introduced. The error may be any failure in linearity, dynamic range, frequency range, energy storage, or time structure. We would like to approach transparency in each of the measures of audio given earlier.
Obviously, we could ensure transparency by over-engineering every aspect (assuming that we know how to), but that would in crease the data rate of the audio signal in the channel.
Given that every digital distribution channel has a bit budget, a designer at tempting to over-engineer is likely to fall into the trap of choosing, for whatever reason, to over-satisfy one requirement at the expense of others, thereby creating an un balanced solution. In the context of DVD Audio, this could easily be done by, for ex ample, providing excessive bandwidth or precision. Neither choice is inherently wrong, but in the real world of storage or distribution, either is likely to reduce the number of channels available for three-dimensional representation. Here we could argue that replacing CD quality with two -channel transparency, without considering the benefits of multichannel, would be a flawed choice for most listeners.
The ARA list presented earlier suggests that it is sufficient to deliver an audio band width of 26 kHz and that precision of at least 20 bits should be used for well-implemented linear PCM channels. Beyond those points, it was felt that further benefits would not accrue until the sound delivered had, by whatever means, been rendered fully three-dimensional.
Having decided what we need in the distribution channel, the question arises of what coding to use. The simplest channel design is one in which all the data in the original recording appears on the disc, which is how very early CDs and some audiophile recordings were made. More often, the original master requires editing, a process that is performed in a digital signal processor whose word size exceeds that of the original (to preserve linearity). In the end, however, it may be necessary to reduce the original's word length in order to fit the signal onto the carrier. This is commonly the case today when 20-bit master recordings must be shortened to 16 bits for CD.
With a maximum reproduction level of (again) approximately 120 dB SPL, Fig. 6 shows the working region for CD. The no table features are a maximum signal level that is uniform with frequency and a smooth, but potentially audible, noise floor. Because the noise floor of a 16 -bit channel can be audible, quantization distortions may, in principle, also be audible. For comparison purposes, I have included plots of the working regions for FM radio (Fig. 7) and vinyl LP (Fig. 8). These analog formats have nonuniform maximum level capability and suffer from substantially higher noise.
REAL-WORLD CD CHANNELS
Let's go back to the earlier example of the incorrectly quantized -90 dBFS, 1-kHz tone and the resulting distortion components. Figure 9 shows the modeled auditory significance of the measurement given in Fig. 4. (Here again, and in all subsequent figures, the acoustic gain is set so as to permit a full-scale digital signal to generate 120 dB SPL at the listening position.) This plot is quite telling: It predicts, for example, that the harmonics generated by the undithered quantization will be significantly detectable right up to 15 kHz. The curve for the un-dithered quantization reveals that the distortion cannot be masked by the signal tone. It is also noteworthy that the harmonic at 5 kHz is nearly 30 dB above threshold.
This implies that there may be circum stances in which the error will be detectable with relatively conservative acoustic gains (lower volume settings).
Single undithered truncations at the 16-bit level are regrettably all too common in practice. Not only do inadvertent truncations arise in the digital filters of very many A/D and D/A converters, but the editing and mastering processes often include level shifts, mixing events, or DC filtering processes that have not been dithered correctly. Thus, there have been reasonable grounds to criticize the sound of some digital recordings, even though this particular defect can be avoided by combining good engineering with good practice.
Figure 10 represents the audible significance of a channel in which a correctly dithered quantization (perhaps in shortening a word from 20 to 16 bits) is followed by a minor undithered process, in this case a 0.5-dB attenuation. You can see how just one undithered process can degrade a correctly converted signal: An audibly raised and granular noise floor is highly probable.
Figure 11 shows how this effect could operate in practice. The upper curve represents the audible significance of the same -90 dBFS tone with all the errors introduced by an original, "correct" 16-bit quantization followed by four undithered signal-processing operations. Four operations may seem like a lot, but this figure actually illustrates a common case in which everyday A/D and D/A converters are used. (As has been mentioned, the digital filters in such converters are rarely dithered.) The upper curve may be taken as a base line of current bad practice in CD recording/playback. For historical context, see Fig. 12, which includes the audible significance of the noise in a silent LP groove.
In many ways, the pity for PCM to date has been that it is so robust, which is to say that the sound survives the kind of abuse illustrated in Fig. 11 because it is superficially the same. If we were to introduce truncation errors like this in other types of digital processing, chaos might well ensue.
(Among other things, computer programs would refuse to run.) Indeed, compressed audio formats that require bit-accurate de livery cannot tolerate the sort of abuse that poor design has brought so routinely to PCM audio.
This analysis of the dynamic range capability of the 16-bit, 44.1-kHz CD channel makes certain things very clear: Undithered quantizations can produce distortions, which are likely to be readily detectable and also quite unpleasant. Undithered quantization of low-level signals will produce high and odd -order harmonics. Undithered quantizations routinely arise in the current CD recording and replay chain, and great care is required if a recording is to be captured, edited, mastered, and replayed with out any error arising.
The basic noise floor of the 16-bit channel suggests that it can be guaranteed in audible only when the maximum SPL is less than 100 dB, as implied by Fig. 5.
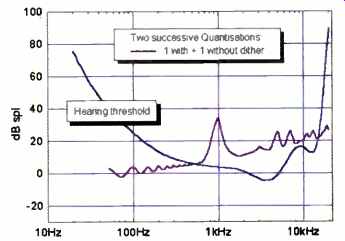
Fig. 10--Audible significance of an undithered, 16-bit requantization
of a 1 –kHz, -90 dBFS tone already correctly quantized to 16 bits at 44.1
kHz.
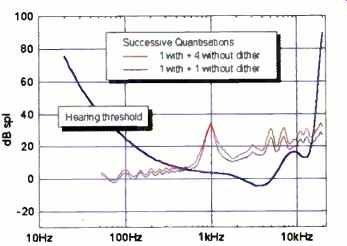
Fig. 11--Audible significance of one (lower) and four (upper) successive,
undithered. 16-bit re-quantizations of a 1-kHz, -90 dBFS tone already correctly
quantized to 16 bit, at 14.1 kHz.
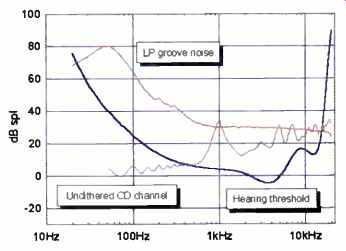
Fig. 12--Audible significance of four undithered 16-bit re-quantizations
of a 1-khz., -90 dBFS tone already correctly quantized to 16 bits at 44.1
kHz., contrasted with the audible significance of LP groove noise.
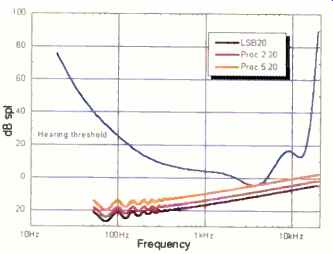
Fig. 13-Audible significance of the noise created by one, two, and five
successive, dithered, 20-bit quantizations.
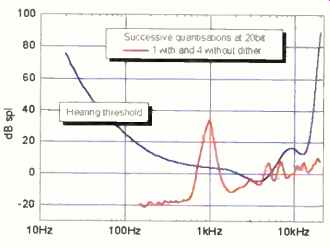
Fig. 14--Audible significance of four successive, undithered 20-bit re-quantizations
of a 1-khz, -90 dBFS tone already correctly quantized to 20 bits al 44.1khz.
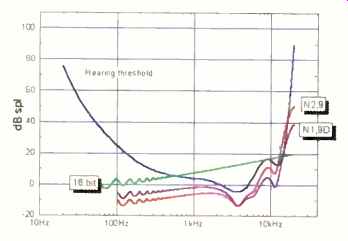
Fig. 15-Audible significance of a simple 16-bit, dithered quantization
plus two examples with noise shaping applied.
20-BIT PCM
Figure 5 also predicts that basic 20 -bit channel noise would be inaudible. Figure 13 investigates the suitability of a 20 -bit recording and replay chain. The channel's basic noise is shown, as is the steady in crease in the noise floor that takes place when the signal is operated on in the channel. The curves represent the effects of one, two, and five dithered quantizations, resulting from one and four operations subsequent to the initial conversion. In fact, a modern system using 20 -bit resolution throughout will probably perform a mini mum of five operations over and above the original quantization process itself, because the A/D and D/A converters will usually contain two cascaded digital anti-aliasing or oversampling filters.
The data used in Fig. 13 suggests that a 20 -bit channel (if engineered correctly) should be capable of providing a transparent and subjectively noiseless sound reproduction chain. This assertion is reinforced by Fig. 14, in which the signal processing postulated in Fig. 11 (a sequence of five quantizations, only the first of which is dithered) is recalculated for a 20-bit channel. This is significant abuse, but it still appears that the distortion components should be barely audible. This is important because it puts an upper limit on the resolution required in a distribution channel.
24-BIT PCM
There is no convincing argument for using 24-bit data in a distribution format.
Figure 13 clearly implies that the noise floor and resolution limit of a 24-bit channel will be 24 dB greater than is necessary.
Why do it, then? One reason would be to provide more data for the subsequent DSP operations to work with. This reasoning is superficially correct. However, I think it is unlikely that A/D converters capable of delivering a 133-dB signal-to-noise ratio will ever be made, and therefore a 24 -bit channel would be kept busy conveying its own input noise! Furthermore, the majority of DSP systems and interfaces use a 24 -bit word length. It is very, very difficult at present to guarantee transparency when performing nontrivial DSP operations on 24 -bit data in a 24 -bit processing environment. Obviously we could develop DSP processors capable of handling longer words, but why should we? Not only is the combination of well-handled, carefully delivered 20 -bit data and a 24 -bit processing environment good enough, but to deliver anything more is virtually to guarantee a higher risk of inadvertent truncation in the average replay chain.
But there's a more pragmatic reason not to distribute 24-bit data: It is virtually certain that the overwhelming majority of DVD players will not pass 24-bit data correctly. Even if they were to use 24 -bit con version, truncation is almost guaranteed, whereas 20 -bit data in the same pathway will pass virtually unscathed.
NOISE SHAPING AND PRE–EMPHASIS
It is possible to exploit the frequency -de pendent human hearing threshold by shaping quantization and dither so that the resulting noise floor is less audible.
Figure 15 shows how the Meridian 518 (an in -band noise shaper) can make a 16 bit transmission channel's subjective noise floor more equivalent to that of a rectangular (unshaped) 20 -bit channel. If such a channel is to be useful, the resolution of the links in the chain before and after the noise-shaped channel must be adequate. In simple terms, this means mastering and playing back using well -designed converters offering at least 2-bit resolution.
It was the view of the ARA committee that noise shaping can be a linear process and that it deserves serious consideration when distribution channels are to be matched to data -rate limitations.
FREQUENCY RANGE
Up to this point, the graphs I've presented have been based on the standard hearing threshold. However, individuals can have somewhat different thresholds; the mini mum audible field has a standard deviation of approximately 10 dB. Some individuals' thresholds are as low as -20 dB SPL at 4 kHz. Similarly, although the high-frequency response cutoff rate is always rapid, certain people can detect 24 kHz.
Figure 16 shows how hearing thresholds can vary. This graph still suggests that a well -engineered, 20 -bit channel should be adequate, bearing in mind that very few rooms, no recording venues, and no micro phones genuinely approach the quietness of the 20 -bit noise floor.
Figure 17 adds the frequency response of a typical D/A converter at 44.1 kHz. This diagram defines the working region of a Red Book CD channel.
DO WE NEED MORE THAN 44.1 kHz?
The high -frequency region of Fig. 17 is shown in detail in Fig. 18. It can be seen that an average listener will find little to criticize regarding the DAC's in-band amplitude response. To acute listeners, a 44.1-kHz sampling rate (even with the extremely narrow transition band shown) means a potential loss of extreme high frequencies (between 20 and 22 kHz). Increasing the sampling rate to 48 kHz does a lot to remedy this.
However, the significance of this has to be questioned. Although there is an area of intersection between the channel frequency responses and the hearing thresholds, this region is all above 100 dB SPL. I know of no program material that has any significant content above 20 kHz and 100 dB SPL! Numerous anecdotes suggest that a wider frequency response "sounds better." It has often been suggested that a lower cutoff rate would give a more appropriate phase response and that the in-band response ripple produced by the kind of linear -phase, steep -slope filter illustrated in Fig. 17 (DAC) and Fig. 19 (ADC) can prove unexpectedly easy to detect. A commonly pro posed explanation is that the shallower high -frequency response rolloffs of analog tape recorders account for a preferred sound quality.
It has also been suggested that the pre-ringing produced by the very steep, linear-phase filters used so far for digital audio can smear arrival -time detection and alter stereo imaging. This pre -ringing shows up in many reviews of CD players. It can be significantly reduced by making the filter less steep (which could be done by increasing the sampling rate) or by not using a linear-phase characteristic.
The research literature contributes very little to this discussion. One well -performed set of experiments by Ohashi has, however, strongly indicated that certain program material may benefit from a system frequency response extending beyond 50 kHz.
The real problem facing researchers is that these experiments are extremely difficult to do. Ultra -high-frequency effects cannot be investigated using existing hardware: Micro phones, recorders, filters, amplifiers, and tweeters would all need to be redeveloped. It is difficult to alter just one parameter, and experiments are hampered by the fact that an ultra -high -frequency -capable chain has yet to be developed to the same level of performance as the current reference.
What can be concluded is that there is some real evidence-and a lot of anecdotal evidence-to suggest that the 20 -kHz band width provided by a PCM channel using a sampling rate of 44.1 kHz is not completely adequate. There is also considerable support for the observation that 48 -kHz digital audio sounds better than the same system operated at 44.1 kHz. This suggests that the 44.1-kHz system undershoots by at least 10%.
My own opinion is that the evidence fails to discriminate between the result of the filtering (genuine listener response to audio content above 20 kHz in air) and side effects of the filtering implementation. A very recent report of certain experiments suggests that, indeed, the side effects are the real culprit.
I have experienced listening tests demonstrating that the sound is degraded by the presence of normal (undithered) digital anti -alias and anti -image filters. I am also aware of careful listening tests indicating that any ultrasonic (i.e., above 20 kHz) con tent conveyed by 96-kHz sampling is not detectable either in the context of the original signal or on its own.
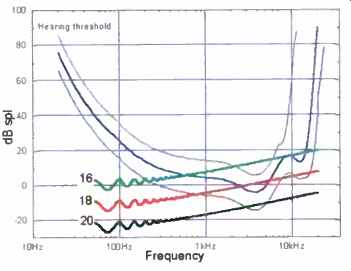
Fig. 16--As Fig. 5.but showing variation created by different hearing
thresholds.
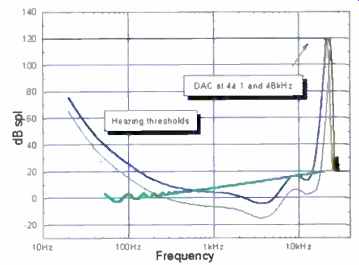
Fig. 17--Frequency response at 44.1 and 48 kHz against the audible significance
of a dithered 16-bit noise floor and average and acute hearing thresholds.
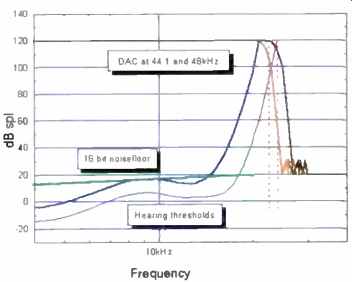
Fig. 18--Detail of the high- frequency range in fig. 17.
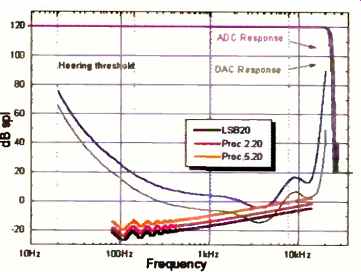
Fig. 19--Useful operating region of a well -engineered 20-bit channel.
The audible significance of noise created by one, two, and five successive,
dithered quantizations is shown against acute and average hearing thresholds.
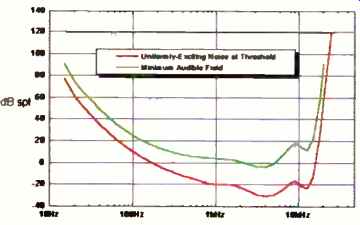
Fig. 20--The average human hearing threshold above a corresponding plot
for the spectrum of the most intense in-band sound that cannot be heard.
Other listening tests I have witnessed have made it quite clear that the sound quality of a chain is generally regarded as better when it runs at 96 kHz than when it runs at 48 kHz and that the difference ob served is "in the bass." Why should this be? Two mechanisms are suggested: aliasing distortion and digital -filter artifacts.
Figures 17 and 19 show the frequency responses of commonly used D/A and A/D converters. In each case, the stop-band attenuation of 80 to 100 dB seems impressive.
But if we invert the curve, we can see that a detectable in-band aliasing product may be generated by signals in the transition region.
Most people listening to PCM signals are listening to channels that do not preserve transparency in the digital filters them selves. Another way of putting this is that we cannot yet reliably discriminate between the phase, ripple, bandwidth, and quantization side effects produced by the anti-aliasing and oversampling filters.
Many of the listening experiences that have raised questions about the high-frequency response of the Red Book CD channel have involved band -limited material, speakers without significant ultrasonic response, and listeners who have a self -declared lack of acuity at very high frequencies. It therefore seems probable that we should concentrate even harder on the methods used to limit the bandwidth rather than spending too much time considering the rapidly diminishing potential of pro gram content above 20 kHz.
This conclusion supports the development of high -resolution recording systems that capture the original at a sampling rate higher than 48 kHz but do not necessarily distribute at so high a rate. Such a system might, for example, benefit from the anti aliasing filters in a 96 -kHz ADC at capture but use different filtering means to distribute at 48 kHz, thereby reaping most of the benefits that could have been obtained by using a chain that operated at 96 kHz throughout. Interestingly, this is exactly how current DVD players work when playing a DVD containing 96-kHz PCM audio.
The signal is carried at 96 kHz on the disc, but because there are not yet standards for a 96 -kHz digital output, the players down-sample to 48 kHz (and usually 20 bits).
PSYCHO-ACOUSTIC DATA
There is very little hard evidence to suggest that it is important to reproduce sounds above 25 kHz. Instead, there tends to be a general impression that a wider bandwidth can give rise to fewer in -band problems. Yet a few points must be raised before dismissing audible content above 20 kHz as unimportant.
The frequency response of the outer and middle ear has a fast cutoff rate resulting from combined rolloff in the acoustics of the meatus (the external ear canal) and in mechanical transmission. There also appears to be an auditory filter cutoff in the cochlea (inner ear) itself. The cochlea operates "top-down," so the first auditory filter is the highest in frequency. This filter centers on approximately 15 kHz, and extrapolation from known data suggests that it should have a noise bandwidth of approximately 3 kHz. Middle -ear transmission loss seems to prevent the cochlea from being ex cited efficiently above 20 kHz.
Bone -conduction tests using ultrasonics have shown that ultrasonic excitation ends up in this first "bin." Any information arriving above 15 kHz therefore ends up here, and its energy will accumulate toward detection. It is possible that in some ears a stimulus of moderate intensity but of wide bandwidth may modify perception or detection in this band, so that the effective noise bandwidth could be wider than 3 kHz.
The late Michael Gerzon surmised that any in-air content above 20 to 25 kHz derived its significance from nonlinearity in the hearing transmission and that combinations of otherwise inaudible components could be detected through any resulting in-band inter-modulation products. There is a powerful caution against this idea, however. As far as I know, music spectra that have measured con tent above 20 kHz always exhibit that content at such a low SPL that it is unlikely the (presumably even) lower SPL difference distortion products would be detectable and not masked by the main content.
WHAT SHOULD THE SAMPLING RATE BE?
Why should we not provide more band width? The argument is simply economic:
A wider bandwidth requires a higher data rate. For a given carrier, a higher data rate reduces playing time or the number of channels that can be conveyed.
To get another perspective on this question, we will take an interesting detour, but it requires acquaintance with two new concepts. The upper curve in Fig. 20 shows the familiar human hearing threshold. Current psychoacoustic theory considers that this hearing threshold derives from two mechanisms. First, the threshold curve's bathtub shape is due essentially to the mechanical or acoustical response of the outer, middle, and inner ear. Second, the threshold level itself is determined by internal noise. The hearing system provides a continuous background noise, which is of neural or physiological origin and which determines the quietest sounds we can detect. Obviously, we do not hear this background noise because the brain normally adapts to ignore it! However, if we were trying to understand human hearing as a communication channel, this noise floor is one of the important parameters. Now, the threshold shape is not what engineers call the noise spectrum but is, instead, the effect of that spectrum. The difference comes from the fact that the human cochlea behaves as though it has a bank of internal filters. These filters are approximately one-third of an octave wide above 1 kHz, and the effect of these filters is to accumulate all the noise around them. If we calculate the noise spectrum that has the effect of the hearing threshold, we get the lower curve in Fig. 20.
This plot shows a noise spectrum that has three fascinating properties. (1) A noise exhibiting this spectral density will be un detectable or, when its level is raised, will be equally detectable at all frequencies; it is uniformly exciting at threshold. (2) This noise spectrum, just below threshold, is the most intense in -band sound that we cannot hear. (3) The "threshold noise-spectral-density (NSD)" curve is analagous to the internal noise of the hearing system.
Taking this last point, we make a further step. Since Fig. 20 shows the effective noise floor of the hearing system, we can now at tempt to specify a PCM channel that has the same properties (in order to estimate the information requirements of human hearing). The point is that if we can model the human hearing communication channel, then that channel must-by common sense-be the minimum channel we should use to convey audio transparently.
Figure 21 re-plots this auditory threshold on a decibel-versus-linear-frequency basis, i.e., a " Shannon plot." The area bounded by the noise floor, maximum level (head room), and maximum frequency in such a plot is a measure of the information or data capacity of the channel. When the noise floor and headroom are flat, we call it a rectangular channel. According to Shannon's theory and to the Gerzon-Craven criterion for noise shaping, this floor can be represented by an optimum minimum channel using noise shaping that conveys 11 bits at a sampling rate of 52 kHz. This straightforward analysis overlooks the fact that if only 11 bits are used, there will be no opportunity for any processing whatsoever and no guard band to allow for differences in system or room frequency response or be tween human listeners. In a sense, the 52-kHz, 11-bit combination describes the minimum PCM channel, using noise shaping, capable of replicating the information received by the ear. Transmission channels need to exceed that performance, so we can argue convincingly that a 58 -kHz sampling rate with 14 bits ought to be adequate if in-band noise shaping is used.
More interestingly, this simple analysis tells us that 52 kHz is the absolute mini mum desirable sampling frequency. For comparison, Fig. 21 shows the channel space occupied by CD audio. It also includes the noise-spectral density of an 18.2 -bit, 96-kHz channel without noise shaping, the minimum noise floor that suggests transparency at that sampling rate.
The conclusion, then, is that both psychoacoustic analysis and experience tell us that the minimum rectangular channel necessary to ensure transparency uses linear PCM with 18.2 -bit samples at 58 kHz. The dynamic range must be increased according to the number of processes taking place be fore and after delivery, and the number of channels feeding into the room, so that we may converge on 20 bits at 58 kHz for five or more channels.
SAMPLING-RATE ISSUES
If we were to be forced, right now, to specify a channel immune to criticism, we would have to: (1) Increase the sampling rate by a margin sufficient to move the phase, ripple, and transition regions further away from the human audibility cutoff.
One could probably make a sensible argument for PCM sampled at 66.15 kHz (44.1 kHz times 1.5). The potential response is shown in Fig. 22. (2) Increase the word length (to 20 bits, for example) so that the audible significance of quantizations, whether performed correctly or incorrectly, will be minimal. Of course, with a higher sampling rate it is not strictly necessary to use a word length exceeding 16 bits. This is because the operating region of a 16-bit, 88.2-kHz (or higher, such as 96 -kHz or even 192 -kHz) channel includes a large, safely inaudible region within which noise shaping can be exploited.
Given that material recorded at high sampling rates will need to be downsampled for some applications (CD, for example), there are strong arguments for maintaining integer relationships with existing sampling rates-which suggests that 88.2 or 96 kHz should be adopted. This would not be an efficient way to convey the relatively small extra bandwidth thought to be needed, but the impact of using these higher rates can be substantially reduced by using lossless compression (packing). Although there is a small lobby that suggests even higher sampling rates should be used, such as 192 kHz, I disagree. When 88.2- or 96-kHz channels have been correctly designed in terms of transmission, filtering, and so forth, higher rates simply will not offer any benefit.
I realize that by expressing the requirements of transparent audio transmission I am nailing a flag to the mast and lay myself open to all manner of attack! However, this analysis has been based on the best under standing to date on this question, and we should exceed these requirements only when there is no detrimental cost to doing so. A Next issue: Part 2 concludes with a look at how transparent PCM audio coding could be implemented for DVD-Audio.
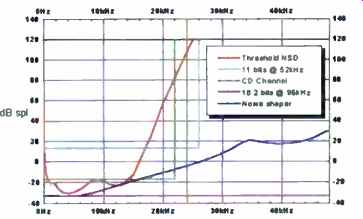
Fig. 21-A Shannon plot of the uniformly exciting noise threshold versus
the characteristics of various PCM channels.
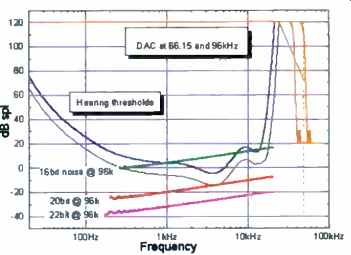
Fig. 22-Charac. of PCM channels using various word lengths and sampling
rates, plotted against acute and average hearing thresholds.
Adapted from 1998 Audio magazine article. Classic Audio and Audio Engineering magazine issues are available for free download at the Internet Archive (archive.org, aka The Wayback Machine)