

By: HERMAN BURSTEIN
The A/B tests reported in Audio and elsewhere try to discover whether, and to what extent, audible differences exist between two similar components such as preamps, power amps, CD players, etc. Very often, a unique device, such as the ABX comparator, is employed to indicate whether a test subject can distinguish between components A and B-say, two power amps. In a number of trials, typically 16, the comparator randomly selects A or B as component X, and the subject must decide whether he is hearing A or B. By pushing designated buttons, the subject can listen to A, B, or X (which is A or B), in any sequence and as often as desired, in order to decide whether X is A or B. Once the decision is made and noted, the subject proceeds to the next trial. The number of trials and the number of correct identifications are tabulated, yielding a score-for example, 12/16, which signifies 12 correct identifications in 16 trials. Studies with the comparator ordinarily employ several subjects, tested one at a time, and they may involve several pairings, such as four amplifiers compared two at a time in all possible combinations. (While it is possible to make such tests by switching the interconnects between the devices under test, such a plug-pulling technique requires the help of a trained and unbiased assistant, introduces hum or r.f.i./e.m.i. problems in many cases, and very often interjects an unacceptably long delay between presentations. making comparison difficult.) The results of these and other NB tests are usually subject to statistical analysis, and it is the purpose of this article to clarify what such analysis can do. First, however, it should be made equally clear what statistics cannot do. Statistical analysis cannot improve the quality of a study, although it may seem to impart a cloak of respectability--"blinding with science," as they say. Statistics can add information to good research, but it adds nothing to poor research. The issue here is the validity of a test, which has nothing to do with statistics. So we'll first discuss validity and then turn to the useful role statistics can play in evaluating the results of valid A/B tests.
Validity and Reliability
Here, the issue is: Does the test really measure what it purports to measure? To illustrate, assume a subject is asked to distinguish between two power amps. The test design must ensure that only audible differences permit him to do so. If this is the case, the test has validity, but if an extraneous factor enables him to distinguish between components, the test lacks validity.
Some examples of extraneous factors are visual or aural clues consciously or subconsciously provided by a researcher who knows which amp is playing (this can't happen if a good comparator is employed), an inadvertent (we hope) but slight difference in level between amps, a significant difference in cables, a click that precedes switching to one amp but not the other, operation at a level exceeding the low-distortion capability of one of the amps, a flaw that develops in one amp during the test, etc. There is no overemphasizing the great care required to achieve validity--to prevent all but the audible differences from clueing the subject as to which amp is which. If a test lacks validity, it cannot be salvaged by statistics.
Associated and sometimes confused with validity is reliability. The issue of reliability is: Are the test results consistent? If a subject distinguishes between components one day but not the next, or if some subjects hear differences and others don't, reliability is poor. Further, reliability is a prerequisite for validity but does not ensure it.
For example, if subjects can consistently distinguish between two amps because of a flaw in one-such as a leaky capacitor that causes audible distortion-we have reliability but not validity. On the other hand, if reliability is poor, validity is suspect.
When a test is considered to have reliability and validity, statistics can help us evaluate the results. There are two mathematically related approaches, and the researcher may use either or both. One approach tests the hypothesis that audible differences between two components truly exist; the other estimates how often a subject (or subjects) hears these differences.
Testing a Hypothesis
We deal here with the significance of test results. The issue is: Are the results due to audible differences or to chance? If we call the results significant, we attribute them to audible differences, not to chance.
In an A/B test, we expect that even a subject who hears no differences and merely guesses which component is playing will, on average, guess correctly half the time; for example, he will make eight correct identifications in 16 trials, for a score of 8/16. If his score is higher-say, 12/16-it seems he hears differences. Nevertheless, a score exceeding 8/16 can be due to chance, just as a coin flipped 16 times can come up heads more than half the time (there is a 40% probability that heads will come up more than eight times in 16 tosses). Thus, we have a dilemma. In our example, is a score as high as 12/16 due to chance or to audible differences? We can resolve this dilemma by using statistics or, more correctly, statistics plus judgment. This is not to deny the role of common sense in some cases. For example, if a subject makes 30 correct identifications in 32 trials, and if we have no question about validity, it would be difficult to gainsay the common-sense conclusion that audible differences very much exist. Still, it is nice to know that the statistical odds against this happening by chance are about 8 million to 1.
To return to the dilemma of whether a score as high as 12/16 is the result of chance or audible differences, we must first restate the problem in statistical terms. This requires choosing between a null hypothesis (Ho), which holds that a score as high as 12/16 is due to chance, and an alternative hypothesis (H1), which holds that a score as high as 12/16 is due to audible differences.
Statistics provides no direct way of indicating whether H1 is true. It can only directly inform us about H0. Whatever it indicates about Ho leads to an opposite inference about H1. This is a seesaw proposition. If Ho is supported, H1 is discredited; if Ho is discredited, H1 is supported. Further, statistics cannot prove Ho to be true or false (and, conversely, H1 to be false or true). As long as we deal with a sample, we deal with the probability, not the certainty, of Ho being correct. Certainty can be obtained only by testing an entire population, not just a sample of it-and then there is no need for statistics, which is concerned with probability, not certainty! In the case of an A/B test, testing the population is impossible, even for one subject, because the population consists of an infinite number of trials.
Therefore, we rely on samples and their attendant probabilities concerning Ho. But small samples can deviate appreciably from the "truth" about Ho.
The larger the sample, the closer it tends to come to the "truth." Statistics supplies the probability of getting a score higher than chance alone would produce: In our example, a score as high as 12/16 instead of 8/16. This probability is termed the significance level, labeled a (alpha); a is the probability associated with Ho being true. If a is sufficiently low, we reject Ho and infer that H, is true: In our example, we would infer that audible differences, not chance, account for a score as high as 12/16. If a is not sufficiently low, we accept Ho and infer that H, is false.
It is of critical importance, prior to conducting an A/B test, to define what is meant by a value of a that is sufficiently low to justify rejection of Ho. This value is called the criterion of significance and is labeled a' (alpha prime). It is critical because it directs us whether to accept or reject Ho, and thereby whether to reject or accept H,. If a is greater than a' (the significance level exceeds the criterion of significance), we accept Ho and thereby reject H,. In our example, this would signify that we lack a sufficiently low probability of getting a score of 12/16 by chance; rather, we believe that chance alone could reasonably account for this score.
But if a is less than or equal to a', we reject Ho and therefore accept H,; we believe that the probability of a 12/16 score being due to chance is sufficiently low to reject Ho and to make H, credible; we believe that audible differences exist.
Where does the value of a' come from? Not from statistics. It comes from our judgment. A widely used convention is to employ a probability of 0.05 as a suitable value of a', although other values are also used. To illustrate, assume that, prior to NB testing, we went along with the crowd by choosing 0.05 as a'; let's also assume that a subject's score is 12/16. We find from the binomial distribution that, for this score, the significance level a is 0.038; that is, if only chance is at work and not audible differences, the probability of getting a score as high as 12/16 is only 0.038. Inasmuch as a is less than a'--i.e., 0.038 is less than 0.05 we call our finding significant; we attribute the score to audible differences.
Suppose a is greater than a'; we would then call our finding not significant and would attribute the score to chance. To illustrate, if a subject's score is 11/16, a equals 0.105, and if we use a' equals 0.05, then we accept Ho because a is greater than a'--i.e., 0.105 is greater than 0.05. Therefore, we reject H, and disclaim audible differences.
Note importantly that our conclusion as to the significance of test results is not based simply on the objective laws of probability. It is also based on a subjective factor, our choice of a'. Although validated by common usage, nowhere is it written that a' must be 0.05. Other values, such as 0.10 and 0.01, are often used.
Suppose we choose to employ a' equals 0.01. We would then call a score of 12/16 not significant because a is greater than a'--i.e., 0.038 is greater than 0.01. We would accept Ho, thereby rejecting H, and attributing the score to chance rather than to audible differences.
Contrariwise, suppose a subject's score is 14/16, and we retain a' equals 0.01. For 14/16, a equals 0.002. Since a is less than a', we judge that our findings are significant, that audible differences exist.
A Matter of Form
There is an issue of good form in stating the significance of findings. Researchers in some fields only state whether the significance level satisfies their chosen criterion of significance--say, 0.05. Thus, their findings are reported either as "significant at the 0.05 level" or "not significant at the 0.05 level." However, this omits vital information: The actual significance level.
If, say, the significance level is 0.002, this is important to know. Or, if the researcher's criterion is 0.05 and the actual significance level is, say, 0.055, this information is more helpful than simply being told the findings are not significant at the 0.05 level. The reader might be satisfied with a higher criterion of significance, such as 0.10, and so the results would appear significant.
Thus, it's good practice to state the actual significance level.
Error Risk
We have stressed that a sample cannot prove anything about audible differences but can only lead to inferences about their existence. When we call findings significant, we are stating a belief that such differences exist.
But, like it or not, we must recognize that judgment has played a critical role in our conclusion, which is based on subjective selection of the criterion of significance, alpha a '.
Accordingly, we must further recognize that sampling entails the risk of error in accepting or rejecting the alternative hypothesis, H,. There are two kinds of error risk; both are important, although some researchers may be more concerned with one kind than with the other:
Type 1 error risk is called a' (yes, the same symbol as for the criterion of significance). This is the risk of rejecting Ho when it is actually true. Conversely stated, Type 1 risk is that of considering H, true when it is actually false, when a subject hears no audible differences.
Type 1 risk is determined by the value we have chosen as the criterion of significance and therefore bears the same symbol as this criterion. To illustrate, if we choose a' equals 0.05, and if only chance (guessing) is at work, then 5% of the time we will erroneously conclude that we have significant results.
The smaller the value chosen for a', the smaller is Type 1 risk--namely, the probability of concluding that audible differences exist when in truth they don't. As one reduces a', one reduces the probability of concluding that audible differences exist.
Type 2 error risk is called 13 (beta). This is the risk of accepting Ho when in fact it is false. Conversely, it is the risk of considering H, false when it is actually true. The magnitude of 13 depends on four factors: Sample size, n. As n increases, G3 decreases.
Value chosen for a'. As a' decreases, 13 increases. Because a reduced a' makes it more difficult to accept H1, rejection of H, becomes more likely.
The score that chance tends to produce--in the case of A/B tests, 50%. The smaller this score, the smaller Beta is.
Effect size, which we may label p'. This is the smallest score that we consider interesting or meaningful. For example, we are not impressed if a subject can score about 52%-barely greater than what pure chance permits-but we begin to be impressed by, say, a score of 70%. In this instance, effect size is 70%. The larger the value chosen as p', the smaller is the value of Beta.
So long as we are sampling, we cannot know whether we have committed Type 1 error by accepting H1, or Type 2 error by rejecting H1. We can only know the risk of each. Prior to sampling, these risks should be adjusted by judicious decisions as to the criterion of significance, sample size, and effect size.
Sample Size
Based on statistical probabilities (on the binomial distribution or on the normal distribution as an approximation of the binomial), one can calculate a sample size to meet all requirements.
To illustrate, assume that a researcher planning an A/B test specifies Type 1 risk of about 0.05, Type 2 risk of about 0.10, and effect size of 70%. (We specify error risks of about 0.05 and 0.10 because sample size and number of correct identifications must be integers, so that the specifications for a' and Beta cannot be met exactly.) The required sample size is 50 trials.
After an A/B test has been conducted, one can evaluate the results in terms of error risk. To illustrate, again assume a score of 12/16, with a significance level of 0.038. If we previously chose a' equals 0.05, we consider a score of 12/16 significant and conclude that audible differences exist.
Type 1 error risk is now the same as a-namely, 0.038. The risk of being wrong in accepting H, is 3.8%; the chance, so to speak, that the subject was always guessing and never heard differences is 3.8%. Still with a score of 12/16, now assume that we previously chose a' equals 0.01, leading us to reject H, and conclude that audible differences do not exist. Further assume an effect size of 70%. In this situation, Type 2 error risk is 0.75. If a subject can make correct identifications 70% of the time in the long run, we run a 75% risk of being wrong in rejecting H1.
An error risk of 0.75 is, of course, outlandish in a search for the truth about audible differences. More attention should have been paid to the design of the A/B test with respect to specifications of error risk, effect size, and resultant sample size. To illustrate, assume that the researcher had specified Type 1 and Type 2 error risks as 0.05 and 0.10 respectively, and effect size as 70%, and had thereby arrived at a sample size of 50. Assume the test produces a score of 32/50. The significance level is 0.032. Inasmuch as he selected a' equals 0.05, the findings are judged significant. Type 1 error risk is 0.032, not far from the specified 0.05. Now assume a score of 31/50, with a significance level of 0.059, leading to rejection of H,. Then the risk of Type 2 error is 0.08, also not far from the specified 0.10. If a score higher than 32/50 were achieved--for instance, 36/50-the significance level would be 0.0013; Type 1 risk of 0.0013 is much better than specified. If a score lower than 31/50 were achieved--say, 27/50--Type 2 risk, for an effect size of 70%, is reduced to only 0.012, much better than specified.
In terms of time and money, A/B testing is costly. Moreover, extensive testing of a single subject within a brief period may bring on fatigue, clouding the results. For these and other reasons-such as availability of personnel-large sample sizes, desirable as they may be, often have to give way to smaller ones, with concomitant increases in Type 1 and/or Type 2 error risks.
A researcher limited to a small sample, with its inevitably high error risks, may keep one risk moderately low by allowing the other to become immoderately high, but both the researcher and the reader should be aware of this. To illustrate, assume that a researcher limited to a sample of 32 trials seeks to challenge the hypothesis that audible differences exist. Further assume that he employs the conventional a' equals 0.05 to avoid reproach for using too rigorous a criterion of significance (such as 0.01), and that he reasonably specifies effect size as 70%. A score of 22/32 is needed to achieve significance; anything lower will produce a significance level higher than the 0.05 criterion. A score of 21 or less will fail to achieve significance and will allow the researcher to disclaim audible differences, but Type 2 error risk here is 0.36. For this test, a denial of audible differences would rest on weak statistical ground.
It is outside the scope of this article to explain the computation of significance level, error risk, and sample size. For these, the reader is referred to my 1988 article [1].
Point and Interval Estimates
A different approach to evaluating the results of A/B tests, either as an alternative or as a supplement to the test of a hypothesis, is the interval estimate, also called a confidence statement. It is often, but not necessarily, accompanied by a point estimate.
These estimates seek to inform us how frequently a subject (or subjects) can identify which component is which.
Clearly, an identification rate of, say, 80% is more interesting than a rate of, say, 60%, even if both of these rates are judged significant.
We may designate pc as the proportion of the time that a subject could correctly distinguish between two components in an infinite number of trials. Based on a sample of trials, the point estimate is a single figure that estimates pc; we may call this estimate pc. The interval estimate consists of two figures that delimit a range within which we believe pc lies. Statistical probabilities (in this case, derived from the binomial distribution) are required for an interval estimate but not for the point estimate.
The Point Estimate
Let n be the number of trials in an A/B test, and c the number of correct identifications. The estimate of pc is simply:

For example, if a subject scores 12/16, we obtain pc equals 12 divided by 16, which equals 0.75.
However, this is not the point estimate we really want, because we know that some correct identifications are apt to result from guesswork. If a subject always guesses, on average his score will be 50%, or 0.50. Let ph be the population proportion of correct identifications based solely on knowledge and not on guesswork. Let pk be the estimate of pk. Then:

Thus, we estimate that the subject can truly distinguish between components, based solely on audible differences, half the time, not three-quarters of the time.
The Interval Estimate
As with the point estimate, we will first deal with an estimate of pc and then with converting this into an estimate of pk.
We have noted that, due to chance, a sample proportion may differ appreciably from the population proportion, especially for small samples. Thus, Pk may deviate appreciably from pc, but the point estimate gives no indication of how much. An interval estimate does indicate how close to the mark we may be by stating a range within which we believe PC lies. This range includes the point estimate. The narrower the interval, the closer we think we are to pc An interval estimate, or confidence statement, has the following two essential components:
Confidence limits, called pc and Pc (p sub-bar and p-bar), are, respectively, the lower and upper bounds of the interval within which it is estimated that Pc lies.
Confidence level, called y (gamma), expresses our degree of belief that pc lies between pc and pc. The value of y is chosen arbitrarily, the most common choice being 95%, although other choices, such as 90% or 99%, are often made.
One of these components without the other is meaningless.
As in determining significance, human judgment plays an essential role in obtaining confidence limits. The higher the value chosen for y, the farther apart are the confidence limits and the wider is the interval estimate. If we choose an extremely high value of γ-- say, 99.9%--the interval estimate tends to become meaninglessly wide, particularly for small samples. To narrow the interval, we must increase sample size and/or adopt a lower value of γ. Seldom is this value lower than 80%. Anything lower--say, 60%--excessively erodes confidence in the stated interval. All in all, we must choose γ wisely, understanding that there is a trade-off between y and the width of the interval. While a high y is desirable, this entails a wider interval, which is undesirable. If we want both a high y and a narrow interval, sample size must be adequately increased.
Loosely, y is sometimes described as the "probability" that pc lies within the calculated interval. Correctly, y means the following, using y equals 95% for illustration: If we were to take a vast number of samples from a population, and each time follow a statistical procedure that employs γ equals 95%, pc would be within the calculated interval 95% of the time and outside the interval 5% of the time. Inverting this relationship, we associate 95% confidence with any one interval estimate.
If, instead, we employ a statistical procedure based on y equals 90%, the interval estimate would be narrower, but pa would lie within the interval 90% of the time and outside it 10% of the time.
To illustrate all this, again assume a score of 12/16. At y equals 95%, then we obtain pa equals 0.476 and P, equals 0.927. In words, we are 95% confident (please don't say "sure" -- sampling never permits us to be sure) that pa is between 0.476 and 0.927.
Recall that our point estimate is 0.75, illustrating that the interval estimate brackets the point estimate.
An interval estimate of 0.476 to 0.927 may be too wide to be meaningful. As already indicated, one way to narrow it is by choosing a lower value of γ--say, 80%. At y equals 80%, we obtain pc equals 0.561 and PC equals 0.886. If this interval is still too wide, the only suitable step (assuming we want both pc and PC) is to increase the sample size. Let's try n equals 64, with the score remaining 75% -- i.e., 48/64. Now we obtain pc equals 0.667 and Pc equals 0.825 at y equals 80%.
Suppose we want both a high confidence level-say, y equals 95%-and a really narrow interval-say, about 4 or 5 percentage points wide. Then the sample size would have to be on the order of 1,000. If n equals 1,000 and the score is still 75% (750/1,000), then pc equals 0.726 and P, equals 0.772 at y equals 95%. The interval has been reduced to a width of 4.6 percentage points at the cost of a tremendous increase in sample size.
Sometimes only one limit is of interest-say, the lower limit. This raises the lower limit somewhat. (If we were interested only in the upper limit, this would lower that limit somewhat.) Returning to our example where we have a score of 12/16 and y equals 80%, we can say that pc equals 0.615--provided we say nothing about Pc. In words, we are 80% confident that the subject can make correct identifications at least 61.5% of the time. This compares with pa equals 0.561 when we make a statement about both the lower and upper limits at y equals 80%.
We now turn our attention to pk instead of pa-namely, to the proportion of correct responses based solely on audible differences. In a manner parallel to equation 2, we may estimate confidence limits pk and Pk as follows, retaining the confidence level employed for pk and pk:

To illustrate, assume we have a score of 12/16, with y equals 80%, pc equals 0.561, and i5 equals 0.886. Then, at y equals 80%,
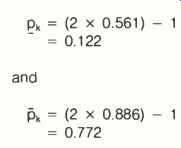
In words, the interval estimate of pk ranges from 0.122 to 0.772 at the 80% confidence level.
Equations 3 and 4 enable the reader to convert binomial confidence limits for pc into confidence limits for pk. The reader interested in obtaining binomial confidence limits pk and Pk, and in determining sample size for an interval estimate, is referred to [2] and [3]. I guess it's time to take a nice deep breath.
References
1. Burstein, H., "Approximation Formulas for Error Risk and Sample Size in ABX Testing," Journal of the Audio Engineering Society, Vol. 36, No. 11, November 1988.
2. Burstein, H., "Transformed Binomial Confidence Limits for Listening Tests," JAES, Vol. 37, No. 5, May 1989.
3. Burstein, H., Attribute Sampling: Tables and Explanations, McGraw-Hill, New York, 1971.
(adapted from Audio magazine, Feb. 1990)
= = = =