By Victor Brociner
In speaker systems using closed and vented cabinets, low-frequency performance is predictable by calculation, which indicates an optimum relationship between speaker area and cabinet volume. This has been confirmed by experiment. Contrary to popular ideas on the subject, performance is not proportional to speaker size.
ASK A Hi-Fi ENTHUSIAST how to improve the bass performance of a speaker system of moderate size, and the chances are he will reply "Get a larger woofer." Surprisingly, when the recipient of this advice follows it, he will probably be disappointed. If he had asked a slightly more sophisticated advisor, he might have been told to use a woofer with greater compliance. In this case, he would be somewhat puzzled at not being able to hear much difference.
Had he been advised to use a smaller speaker, there would be no need to discuss the result of the experiment because he would have concluded that the "expert" was joking, or crazy.
But if he had taken the trouble to try it, and certain conditions had been met, he might have been agreeably surprised.
Is this affront to our customary worship of size supported by the facts? Fortunately, the low-frequency performance of speakers is fairly simple to calculate, so we can proceed to make a series of experiments-on paper-to explore this problem.
Afterwards, it will be of interest to test our conclusions experimentally.
The Requirements
First, what do we mean by "moderate size?" Bookshelf-type speaker systems have internal volumes in the range of 0.5 to perhaps 3 cubic feet. This class of speaker is extremely popular, and warrants our primary attention.
Second, what is meant by "improving the bass response?" We assume that this comprises:
1. Extending the frequency response to a lower limit.
2. Maintaining a smooth response, without peaks and with a minimum amount of roll-off.
3. Keeping distortion within acceptable limits at reasonably high power levels.
Basic Theory
The acoustic output of a direct radiator speaker is expressed by the formula:
Where
P_A= R_A U^2
P_A = acoustic power in watts
R_A=radiation resistance in mks rayls (acoustic ohms)
U =rms volume velocity in m^3/ sec
and RA = [2 pi rho f^2] / c for low frequencies
where rho =density of air in kg/m^3
f =frequency in Hz
c =velocity of sound in m^3/sec
Also U ( volume velocity) = Av
where A = area of the cone in m^2
v=velocity of the cone in m/ sec
Figure 1 shows that at low frequencies the radiation resistance slopes upward at the rate of 12 dB per octave. The dashed line shows the high cone velocity at resonance, followed by a downward slope that becomes 6 dB per octave in the so-called mass-controlled region of operation. The power output, derived from these curves by the formula given above, is shown by the solid line.
This is the frequency response of the speaker assuming piston action, that is, no cone break-up which is a valid assumption for the lower part of the curve at least.
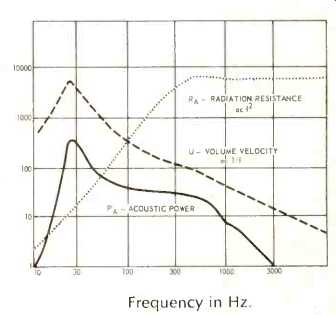
Fig. 1--Calculated performance of piston as a direct radiator.
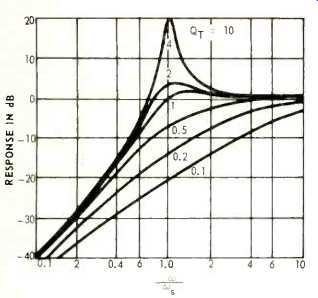
Fig. 2--Frequency-response vs. Q.
The response at resonance relative to the flat section of the frequency-response curve is determined by a single parameter: the Q of the speaker amplifier combination. As in all resonant circuits, the higher the peak, the narrower it is. A family of response curves for different values of Q is shown in Fig. 2. Critical damping occurs for Q=0.5; for this condition, the curve has no rise above the flat portion of the curve. It is down 6 dB at resonance and drops off at 12 dB per octave below this point. For Q= 1, there is a slight rise above resonance--about 1 dB-and response at resonance is equal to that in the flat range. As a matter of fact, the response at resonance is given by a simple expression:
20 log10 Q
It is seen that for values of Q greater than one there is a peak at resonance; while for values less than one, response is down at resonance.
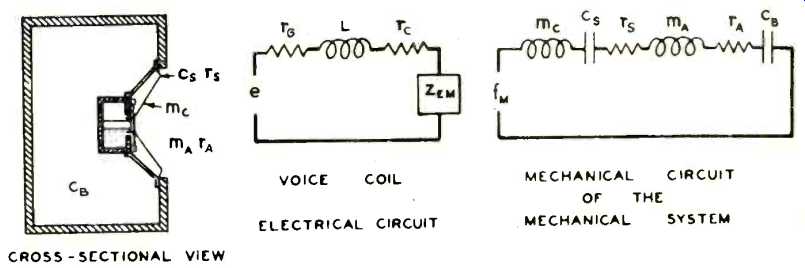
Fig. 3--Analog circuit of speaker mounted in a closed box.
Closed Box
The curves apply to a speaker in a true infinite baffle, or in a closed box, radiating into a hemisphere. As is well known, placement of the speaker at a wall-floor junction or in a corner of a room tips the bass response upward.
The resonant frequency referred to above is that of the speaker-box combination and not just that of the speaker. When a speaker is mounted in a closed cabinet of moderate size, the air in the box behaves like a spring acting against the motion of the cone. The inverse of the stiffness of this air spring is the compliance of the box. It is proportional to the volume of the enclosure. The compliance of the speaker-box combination is less than that of the speaker alone, raising the resonant frequency. Figure 3 shows the direct analog circuit of a speaker mounted in a closed box. The moving mass of the speaker is represented by an inductance, while capacitances correspond to compliances. The box compliance is in series with the speaker compliance, resulting in a total compliance that is less than either of them.
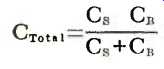
Typically, C_B may be 1/8 Cs. Then C_Tot =1/9 Cs as
The resonant frequency fr= 1/2 pi __/mC
where m=mass in kg
C=compliance in m/n (meters per Newton of force)
Since f_r is inversely proportional to the result of decreasing the compliance to 1/9 its original value is to raise the resonant frequency to three times its original value. A speaker with a free-air resonance of 20 Hz in the box used as an example would have a system resonance of 60 Hz.
When a speaker is connected to an amplifier, the Q of the combination is lower than that of the speaker alone.
Typical hi-fi amplifiers have such high damping factors, or to put it another way, such low source resistances that they can be considered virtual short-circuits as far as speaker Q is concerned. Under these conditions, the amount of additional damping provided by the amplifier is almost completely determined by the voice-coil resistance. The Q of the amplifier-speaker combination is related to the speaker Q as follows:
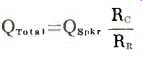
where R_c=resistance of the voice coil
R_R=resistance at the peak of the resonance curve
Suppose that the speaker taken as our example is critically damped (Q=0.5) when in its enclosure. Its frequency response is shown as curve 1 in Fig. 4. How can better bass be obtained? Obviously, by increasing the size of the enclosure. But we have ruled this out. The problem is what to do about the speaker, not the box. The effect of the stiffness of the box can of course be reduced by making the speaker stiffness greater. It might be made equal to that of the box, that is, eight times as great as before. Then the box will only halve the original compliance, and the frequency of resonance will only increase by a factor of _/2 instead of 9, as before. The trouble is that when the speaker stiffness is increased by a factor of 8, its free-air resonance is increased by _/8 to 56 Hz. The box now raises this by only _/2 to 78 Hz, resulting in Curve 2; obviously we are worse off than before. We might have known that nothing can be gained by increasing stiffness. But we can learn something interesting if we look at it in reverse: decreasing speaker stiffness gains very little as long as the box stiffness is the controlling factor and the mass of the speaker's moving system is not increased. "Low-resonance" woofers with light moving systems do not provide good bass response.
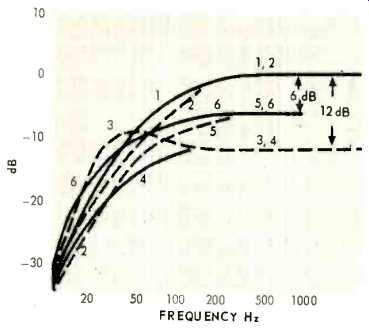
Fig. 4--Calculated frequency response of speakers of different parameters
mounted in a closed box.
We might try to increase the stiffness by a smaller factor, say 4, and increase the moving mass by 4 (without changing the voice-coil driving system) so as to retain the original 20-Hz free-air resonance. Now the box increases the total stiffness by a factor of only _/3, the ratio of system to speaker resonance is only V and the net resonant frequency becomes 20 x _/3=35 Hz. This looks good.
What has it cost? The mid-frequency of a speaker is inversely proportional to the square of its moving mass. This has been multiplied by 4, so the efficiency is lowered by 12 dB. See Curve 3 of Fig. 4. Note that the curve shape is different. Something has happened to the Q.
Q= 2 pi fr m / R_M
Where:
fr =resonant frequency
m =moving mass
R_M =total resistance
The mass m has been multiplied by 4, f, has been divided by 60/35, so the new Q=4 x 35/60 x 0.5 or about 1.2. The Q could be reduced to 0.5 by increasing the damping mechanically, acoustically, or electrically.
Both damping and efficiency could be improved by using greater flux density; this is a fairly expensive expedient.
What else could be done? A more detailed examination of the box compliance is in order. If it is assumed that the box can be represented by a pure compliance, which is reasonably true at low frequencies for enclosures that are not disproportionately long or narrow,
C_A= V/rho c^2
where V =volume of the box in m^3
p =air density in kg/m^3
c =velocity of sound in m/sec
This assumes that the box contains comparatively little sound absorbing material. The correct amount of appropriate material can increase the box compliance by a factor of 1.4 Dimensionally, CA is in units of d^5/F where d=distance and F=force.
We are used to stating compliance in terms of d/F or distance per unit force. Let this mechanical compliance be C_M.
Then
C_A=d^4-=d^4 CM
Since d^4 represents an area squared we can write
C_A (acoustical compliance)=A^2 CM
where A=area
But what area? Well, what we want to know is the effect of the box on the speaker. So the area must be that of the speaker. Hence,
C_M (mechanical compliance) = C_A/As^2
Intuitively, the result is obvious. If we apply the same hand pressure, first to a small piston and then to a large one when both are mounted in boxes of equal size; the box will feel much stiffer (less compliant) with the large piston than with the small one.
The compliances used in the analog circuit of Fig. 3 are mechanical compliances. Consequently we can make the box compliance look greater by reducing its area. Going back to the original example in which the box compliance was 1/8 that of the speaker, suppose that the speaker diameter is reduced by a factor of 0.707 and all other parameters kept the same (including the mass). The new area is one-half that of the original speaker. The mechanical compliance (of the box) seen by the speaker is multiplied by the square of the compliance ratio (new to old) or 4. Instead of 1/4, the box compliance is now 1/2 that of the speaker, and the new system resonance is 20 13 or 35 Hz.
What has been lost this time? Reducing the cone area by t/2 cuts the radiation resistance to I/ of its former value. The efficiency is decreased by 6 dB. The frequency response is shown by Curve 5. The Q is reduced to about 0.3 and the frequency response is more nearly flat than that of the original speaker. Decreasing the damping to restore Q to 0.5 would result in Curve 6. The power handling capability of a speaker is proportional to the square of the area, so this has been reduced to i/ the original value, assuming the permissible voice-coil excursion is as great as before.
The speaker designer can juggle many parameters to obtain the desired compromise among frequency response, curve shape, efficiency, power handling capacity, and cost.
The speaker purchaser cannot easily specify or even determine some of these factors. Most moderately priced° woofers of the "high-compliance" type are likely to be under damped, so there is not too great a probability that system Q's will be appreciably less than 0.5. If the box size is fixed, frequently the bass response can be most easily improved by using a smaller speaker, provided one is willing to sacrifice some power handling capacity.
Vented Box
The vented, ported, or ducted box, or bass reflex cabinet is also capable of analysis in terms of analog circuits and families of curves. For a box tuned to the speaker free-air resonance, the equation is
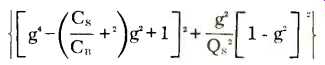
where: Cs =compliance of box
Cs =compliance of speaker
g =f/fr
fr =free-air resonant frequency of the speaker.
Q_S =Q of the speaker in free air, connected to the amplifier.
It is now no longer possible to draw one family of response curves because there are two parameters-the speaker Q and the ratio C_s/C_B. Typical response curves have been published by James F. Novak of Jensen' and are reproduced here, slightly modified, in Figs. 5, 6, and 7.
These curves appear quite complicated to interpret, but a study of them reveals that some interesting generalizations can be made. The first is fairly obvious: for small cabinets where the speaker compliance is several times the cabinet compliance, the speaker circuit Q must be between 0.3 and 0.4 for smooth response without peaks. Higher values can result in violent peaks, as in the case of the closed box. For boxes of moderate to small size, the peak is given approximately by:
SPL=10+20 log Qa
for low values of Q. For example, a Q of 1 produces a 10 dB peak which is accurately given by the formula.
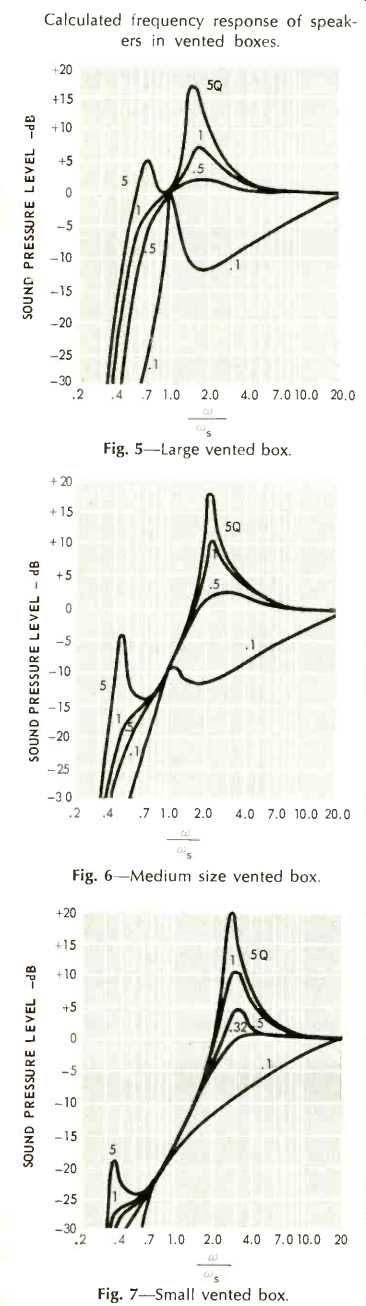
Fig. 5-Large vented box.
Fig. 6-Medium size vented box.
Fig. 7-Small vented box.
This peak occurs at the upper resonance mode of the system, corresponding to the upper peak in the well-known impedance curve. For practical boxes this occurs at 2 to 3 times the resonant frequency of the system with the vent closed. The peak thus can easily be in the vicinity of 90-100 cps, where it causes an extremely annoying booming effect, with a great deal of hangover. This is a cogent reason for maintaining values of Q down to the previously mentioned values of 0.3 and 0.4.
How far down can one expect the bass response to go? At the speaker resonance, the sound pressure level referred to mid-frequency response is:
ΔSPL=20log10 CS/CB
Fig. 8 if one considers Curve 2 the original response and Curve 1 the curve resulting from a lower resonant frequency. The responses at 40 Hz are nearly identical. (It is assumed that the box is always tuned to resonate at the free-air resonant frequency of the speaker.) As with the closed box, increasing mass reduces efficiency and raises the Q, requiring more damping, and lowering output by 12 dB, as illustrated by Curves 3 and 4.
The last alternative illustrated comprises improving the box/speaker compliance ratio by increasing the box compliance-not by making the box larger, but by using a smaller speaker. Curve 5 is for a speaker of half the original cone area. The frequency response is the same (Curve 4) but the loss of output is only 6 dB. Comparing the closed and vented boxes, it is apparent that the latter provides flat response to a somewhat lower frequency, with a sharper low frequency cut-off. The vented enclosure has three parameters in place of the two of the closed box, affording the designer more flexibility in optimizing bass response. On the other hand, it can be seen from the curves of Fig. 8 that a relatively small deviation from the correct values of the parameters of the vented box can result in large deviations from flat response, which is not the case for the closed box.
Experimental Results
In order to test the theoretical conclusions by experiment, a woofer was constructed with a 3 3/4-inch diameter cone and a free-air resonance of 34 Hz. This required a very large surround; since a part of the surround moved so as to radiate an appreciable amount of sound, the effective cone diameter was actually about 4 1/4 inches. This woofer was mounted in a 0.6 cubic foot cabinet tuned to 34 Hz by means of a port with a cylindrical duct. It was realized, of course, that the small power-handling capacity of this speaker would make it an impractical design; the extreme conditions were imposed to make the comparison with a large speaker more striking.
The frequency response up to 1000 Hz was measured and compared with that of a heavy 15-inch woofer in a 4 cubic foot vented enclosure. In Fig. 9 the dashed lines depict the response in an anechoic chamber and the solid lines show the performance in a typical living room. Listening tests were conducted with the speakers concealed behind a sound permeable curtain, with signal levels adjusted for equal acoustic outputs.
At moderate sound levels below the overload point of the small woofer, it was not possible to distinguish its bass response from the large system.
The author wishes to thank Daniel von Recklinghausen, Technical Director of H. H. Scott, Inc., for his invaluable assistance in providing the necessary computer calculations of the data plotted in Figs. 4 and 8.
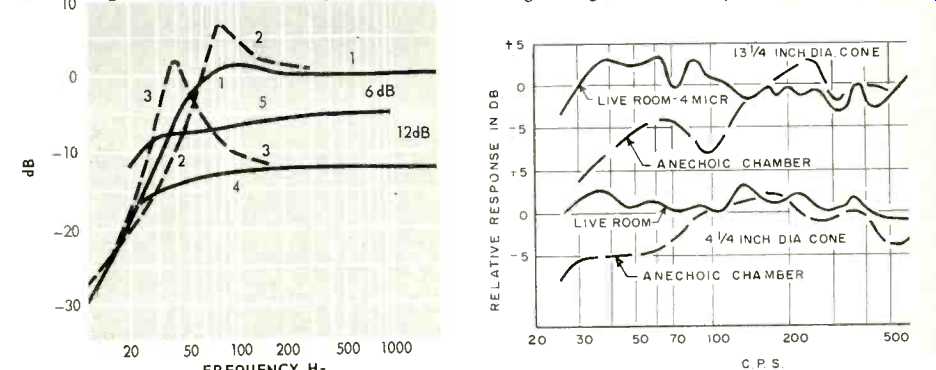
Fig. 8--Calculated frequency response of speakers with different parameters
in a vented box.
Fig. 9--Relative response curves of a small and a large speaker.
FOOTNOTES
1. Performance of Enclosures for Low-Resonance High-Compliance Loudspeakers--James F. Novak-IRE Transactions on Audio-Jan-Feb 1959.
2. This experimental speaker was constructed and measured while the author was Engineering Manager at University Loudspeakers, Inc.
(adapted from Audio magazine, Mar. 1970)
Also see:
That Damping Factor (by Paul W. Klipsch) (Mar. 1970)
Some Loudspeakers Past and Present (Apr. 1970)
The Loudspeaker as a Spherical Sound Source (Mar. 1973)
Layman's Guide to LOUDSPEAKER SPECIFICATIONS--Part 3 (conclusion) (Jan. 1970)
= = = =