by Norman Crowhurst
BY THE NEXT TIME George wandered in Henry's office, when neither of them were too busy, George had been thinking quite a little about their earlier discussions on calculations associated with electronics.
"You know," George opened the conversation, "when I took some course in mathematics for electronics, or whatever it was called, there was one thing that always left me in the air. It strikes me now that perhaps you could help me understand it." "What's that?" questioned Henry.
"Maybe it's really more than one thing, but they all relate to calculations involving reactances," George responded. "I don't know, somehow I've drifted into depending on charts of one kind or another and, if I can't find a handy-dandy chart that just suits my needs, I'm lost. Of course, it is always nice to have a chart do the work, but I'd be a lot happier if I knew what work the chart did for me." "You mean you're always afraid, when you don't know what you're doing, that you might misuse the chart, because you don't understand what it's supposed to do?" asked Henry.
"That's about it." "So ask me-perhaps we can figure it out," said Henry.
"I think the first thing that bothered me is that 2-pi bit and `angular frequency' or something, in the formulas for reactance of inductances and capacitances. Then, when you get past that, there's the whole vector addition bit, where you add quantities together, but they don't follow the rules of addition." "Let's take one piece at a time," suggested Henry. "The word `reactance' means something fundamentally different from `resistance'. A resistance ‘solidly' resists current flowing through it. The voltage that `registers' that resistance is always strictly proportional to the current that causes it. If a resistance is 100 ohms, and the current 20 milliamps, then voltage will be 20 x 100 = 2,000 millivolts, or 2 volts. That's true at every instant, in a resistance, no matter how voltage and current change.
"But in reactances it's different. It is not current or voltage that directly produces a voltage or current effect, as in resistance, but change of current that produces voltage, or vice versa.
Let's take inductance first. A Henry--the unit of inductance--is defined as having a value that, when current changes at 1 amp per second, the reactive voltage generated is 1 volt." "Yes," responded George, "I remember that bit, now you repeat it, but from there on, the whole thing lost me, pretty fast. The teacher got into the angular measure of angles ` or something ...." "You mean the circular measure of angles, as opposed to the more conventional `degree' measure," suggested Henry.
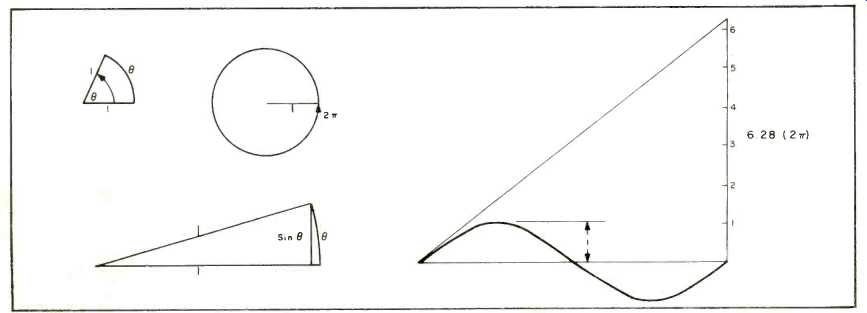
"I guess that's it," George said, "And then a 2-pi got in there, and I never could see how frequency got into the picture. I used the formula for quite a while, without knowing why, and then I found charts took all the trouble out of it, but I've never been happy about it." "First let us look at the circular measure of angles," suggested Henry, as he started to draw. "Really, it's the degree measure that starts the difficulty. There is no real reason, except that somebody a long while ago did so quite arbitrarily, for dividing a circle into 360 equal parts called `degrees' or a right angle, which is a quarter-or 'quadrant'-of a circle, into 90 of them.
"The circular measure of angles simply takes a radius, rotates it from its starting point, so one end stays at the center and the other end follows the circumference of a circle, and the movement along the circumference, measured with the radius as unit length, describes the angle made."
Henry was drawing as he did this, and George picked it up. "Oh, I see, so when you've completed a circle, which degree measure calls 360 degrees, the circumference is 2-pi times the radius that draws it?" "That's the idea," said Henry. "So far, so good. Now we come to apply that to a sine wave." "That's another place where I got lost," said George. "Nice neat 30, 60, 90 degree angles, with 45 in there somewhere, made easy figuring, but this `pi radian' bit lost me." "Do you remember the ratio that defines the sine of an angle?" asked Henry.
"Yes," replied George, "in fact that is all I can remember of my trig studies, I think. The sine is the ‘opposite over the hypotenuse'." He drew it as he said it.
"Now," said Henry, if the angle is small, as it is when it's crossing from negative to positive, near zero, the hypotenuse is the same as the radius, and that little bit of `opposite' and the little bit of circumference are the same thing, for the time being, aren't they?" George could see this, so Henry switched his attack and drew out a sine wave. "So the rate at which the sine is changing, where it crosses the zero line, is the same as the rate at which the angle is changing, when you use circular measure, instead of degrees." George did not say anything, so Henry went on.
"Now, if this rate of change did not change, how big would the sine be, by the time you completed a circle, or period of some frequency?" And he drew a complete sine wave, with a tangent going on up.
"Two-pi?" suggested George.
"Right. Now remember that change of current is what causes voltage, in an inductive reactance. Maximum change is where the sine wave crosses the zero line, as shown by maximum slope at that point. And extending it like this shows that, if this rate of change kept up for the whole period-of whatever the frequency--the change would be 2-pi units." "Come again," said George, "I'm not quite with you." "Suppose," said Henry, "the maximum current, at the peak of the sine wave, is 1 amp, and the frequency is 1 Hz, or 1 cycle every second. Then the rate of change where the current crosses the zero line, is 2-pi amps per second." "Daylight is beginning to dawn," said George. "Go on." "Now, if the frequency is 60 Hz, then each cycle takes 1/60th of a second, so the rate of change, where the current crosses the zero line, is 2-pi times 60, times the maximum current at the peak of the sine wave." "Got it," said George. "So 1 Henry will have a reactance of 2-pi times 60--what's that, a little more than 360 ohms?--at line frequency." Henry showed George how putting the `pi' mark on the 'C' scale of his slide rule by the '5' on the 'D' scale put 1 on the 'C' scale opposite `6.28' (approximate value of 2-pi) on the 'D' scale, and then that '6' on the 'C' scale came opposite 3.77 on the D scale.
"More precisely," he said, "it's 377 ohms." "It's making sense now," George said. "I could follow the part that showed that maximum voltage appeared at zero current, because that was where current was changing fastest.
It was how the 2-pi got into the relationships that bothered me. That whistle will be blowing anytime now, to summon me back to work, so I must reserve the getting of capacitive reactance straight for another time. Then there's that `operator-j' bit. I never did understand that, although guys who did, seemed to do some pretty cute tricks with it and save a lot of time." Just then the whistle did blow, so they parted for the time being.
(adapted from Audio magazine, Apr. 1972)
Also see:
= = = =