
Starting with this issue, I am privileged to share with you the results of
a series of tests and evaluations of various microphones. This is a pleasure,
as it allows me to pass along some of what I learned as an engineer in RCA's
Acoustics Laboratory. You may well recall from the recent historical article
in Audio by Bob Paquette (Dec., 1974) that RCA and Western Electric were leaders
in microphone development in the 1920s and '30s. I was a latecomer, joining
RCA in 1957, but was fortunate to work with several of the great pioneers in
acoustics.
I discovered that development of specialized precision test apparatus had paralleled developments of commercial microphones. These instruments were never described in the literature, probably because they are less interesting than commercial microphones or other products. We use some of these unique instruments in our testing, and I will attempt to fill in the literature void by describing them in detail.
Our title hints that our evaluations may not be as thorough as we'd like. A microphone is a personal instrument, handled, fondled, dropped, or used as a hammer by humans. Our test may show that a microphone has superior technical characteristics for a given application, but the user must be the final judge. If the microphone does not look, feel, or sound right to you, then it is not the best instrument for your purpose.. Sometimes your application may involve stresses or environmental factors that we did not anticipate in our testing Microphone performance requirements are varied and numerous, and only rarely does one particular model fulfill all requirements.
Looking at the brighter side, I have been testing microphones for 20 years and have no connection with any product manufacturer. I a am under no pressure to "go easy" on advertisers.
(Editor's Note: Oh, drat!) Therefore, I can serve you, the reader, as a qualified and unbiased consultant on microphone select on. Our tests will be as accurate and complete as possible. I hope to earn your confidence. Reader comments and questions are invited and will be welcome.
Testing Methods-Standard or Special?
General principles and methods of testing microphones are well established in the standards literature, which is listed in the table. The ANSI document, in particular, is a detailed and up-to-date "cookbook." There is no need to develop additional, more sophisticated tests. This situation is different from evaluation of loudspeakers, where the standards literature leaves much to be desired. We hope that the novel and excellent methods developed by Dick Heyser and presented in Audio will, in the future, be adopted as national and international standards.
However, even a reader with an engineering degree can learn few specifics of microphone testing from the standards documents. This is good because standards must allow for continuing refinement in test apparatus. Each laboratory must engineer their own test facilities. You will find a mixture of off -the -shelf instruments plus numerous custom instruments and test fixtures. Each lab claims conformance to standards, but the differences between laboratories are great enough to account for significant inconsistency in published data. Add to this the sales department's very natural desire to smooth out the wiggles in the frequency response curves, and you end up with catalog literature that cannot be used for reliable comparisons of performance.
(Editor's Note: I wish you hadn't said that; it means another ulcer.) Our tests may not be more accurate than Manufacturer "X," but we use the same instrumentation to test brands "X," "Y," and "Z," so the results may be precisely compared. In addition, we promise to publish all of the wiggles we find!
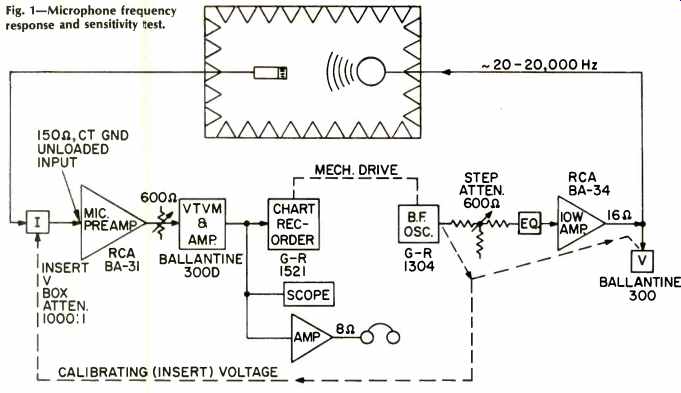
Fig. 1-Microphone frequency response and sensitivity test.
Sensitivity Ratings
According to ANSI S1.10 the Free -Field Response Mf of a microphone at a particular frequency is defined as:
Mf = e/Pf
where e is the open -circuit output voltage and Pf is the free field sound pressure which existed prior to introduction of the microphone.
This must be converted to decibels so that the data can be plotted on a standard graph of a dB versus frequency. The desired quantity is the Free-Field Response Level Rf (unit is the decibel.)
Rf = 20 Login10 Mf/Mr
Mr is the reference level which is 1 volt per newton per square meter. The Pascal 1Pa) is equal to one newton per square meter. Rf is expressed in decibels with reference to 1 volt per Pascal. This may be abbreviated to dBV/Pa.
Example: A rated sensitivity of -60 dBV/Pa means that for an input of 1 Pascal (+94 dB Sound Pressure Level re 20 micro pascals), the open -circuit output of the microphone is 60 dB less than 1 vo t, or 1 millivolt.
Note: The above are S.I. (International) units. You will find many specifications use the older c.g.s. units where Mr equals 1 dyne per square centimeter or 1 microbar. 1 Pascal equals 10 microbars. Thus, with 20 dB less input, the microphone will have 20 dB less output (Rf), and the sensitivity figure becomes -80 dEV/microbar.
The open-circuit output e is essentially equal to that obtained with a preamp whose actual input impedance is much greater, say 10 times, the actual impedance of the microphone at any frequency. This is known as an "unloaded input" circuit. Most audio equipment designed for low impedance microphones has "unloaded inputs." Infrequently we find equipment where the manufacturer has provided "matched" input impedance. You should generally avoid purchase of such equipment because the frequency response of such microphones may be degraded.
The open -circuit response level in dBV/Pa is the fundamental microphone sensitivity rating. The others were described it great detail by A. Lorena in the December, 1976, issue, and I will not cover the same material. I will however correct some errors and omissions and emphasize just two of the coatings.
You have observed that sensitivity is rated for 1 Pascal or 94 dB Sound Pressure Level, which as indicated corresponds to a very Vouc" voice at one toot. The important correction to be made to Lorona's article is that standard speed level (per ANSI Standard S1.8-1969) is 65 dB at one meter, which results in 75 dB at one foot. The discrepancy between the 75 and 94 dB levels is a well-known bi: of non -realism in the Standards.
The dBV rating works for both high- or low-impedance microphones. There is an additional useful rating for low impedance microphones that I call "Power Sensitivity," which is expressed in dBm:
Power Sensitivity equals the power output level in decibels with reference to 1 milliwatt (dBm) that would theoretically be obtained if the microphone was operated into a matched load with a sound pressure input of 1 Pascal.
"Theoretically" refers to the assumption that the microphone impedance is equal to rated value, and that the load value equals this value. In practice, the microphone is unloaded, so the dBm value is thought of as "power available" to a matched load.
Table 1--Standards relevant to microphone testing.
ANSI 51.10-1966 R1971: Calibration of microphones.
EIA SE-105: Microphones for sound equipment.
EIA RS-221: Broadcast microphones, Polarization or phasing of.
ANSI-American National Standards Institute.
EIA-Electronic Industries Association.
Example: Assume our -6G dBV/Pa microphone is 250 ohms impedance. (This yields round numbers, unlike the 150 ohm value that is widely used.) 1 milliwatt into 250 ohms develops 0.5 volts. The open circuit value is 1 volt. Thus, -60 dBV equals -60 dBm. The Power Sensitivity or dBm rating equals the dBV rating if the microphone impedance is 250 ohms.
The third sensitivity rating of significance to all microphones is the EIA Sensitivity rating (GM). It is calculated from our (S.I. units) dBV rating Rf:
GM = Rf - 20 - X
X is from a table in EIA Standard SE -105. For microphone rating impedances from 75 to 300 ohms, X equals 71.8.
Example: Our microphone with Rf = -60 dBV/Pa and (150 or) 250 ohms impedance has GM= -60-20-71.8=-151.8 dB
What is the utility of this strange number? It turns out to be very useful for by adding the Sound Pressure Level (SPL) input to the GM value, you obtain the approximate dBm output (into that fictitious matched load).
Example: You are expecting to record a rock group with the above microphone and anticipate a maximum SPL of 120 dB. Your recorder overloads at 15 millivolts input. Do you need an attenuator between mike and recorder? Adding +120 to -151.8 we obtain -31.8 dBm "Power Output." Recalling that dBm equals dBV for a 250 ohm impedance, the open circuit output of the mike is -31.8 dBV or 25 millivolts.
This will overload your recorder so you need an attenuator.
(You may check this result by noting that 120 dB is 26 dB greater than 94 dB (1 Pascal). The mike output is -60 dBV for 1 Pa, and thus the output for 120 db SPL is -60 +26 or -34 dBV. This is close enough to 31.8 dBV for practical purposes.) In the event that arithmetic is not your bag, I suggest the Shure SRC -1 Sound Reinforcement Calculator. This excellent cardboard computer relates all three of these sensitivity ratings and will tell you millivolts output versus SPL. Just remember to add 20 to the dBV numbers; Shure uses c.g.s. instead of S.I. units.

Fig. 2-Photo of measuring rack.

Fig. 3-Small sound source and 640AA.
Frequency Response and Sensitivity Test
The object of this test is lo measure microphone response level, Rf versus frequency. The 1000 Hz value of Rf is generally the published sensitivity. The frequency response is simply the plus or minus variation of Rf compared to its 1000 Hz value. (Fig. 6).
Figure 1 shows a diagram of our instrumentation, and Fig. 2 shows the author at the controls. The heart of this system is the precision Spherical Sound Source shown in Figs. 3 and 4. It was developed 29 years ago by A.L. Witchey.
It consists of a 2 -in. diameter aluminum dome diaphragm attached to its periphery to a tapered thickness aluminum coil form that was machined from bar or tubing. The coil is long compared to the magnetic gap. The moving system is suspended by three loops of nylon thread which fasten at six points around the front and rear of the coil form.
Precise tension adjustment is provided by adjustable pulleys and screws accessible from the outside. In the photos, you can see the suspension housings projecting radically from the dome. The resonance of the moving system is extremely low; if you displace it by a d.c. current, it may take a minute to return to rest position! Damping is high because of eddy currents induced in the solid metal coil form.
This source is essentially a combination of a dome radiator and an acoustic suspension low frequency speaker. (And you thought these were new concepts.) This arrangement results in low frequency response in excess of that normally expected from a 2-in. radiator, and in very smooth frequency response.
The calibration of this source is shown in Fig. 5. Some broad band equalization is employed, but it is not practical to flatten the response below 100 Hz. Microphones, particularly directional types, have a proximity effect (see Fig. 9) that provides "bass boost" which offsets the source response below 100 Hz. Thus, we can calibrate some microphones down to 40 Hz with this source. The rising high frequency response is an artifact resulting from an old error.
This could be equalized flat if we choose to do so.
Returning to Fig. 1, note that the "EQ" for the sound source is inserted ahead of the power amplifier. The oscillator is driven by the recorder and slides slowly from 20 to 20,000 Hz. The frequency is synchronized with the chart. A sample chart is shown as Fig. 6. How do we calibrate the decibel scale so we can calculate the JBV and other sensitivity numbers? All we need is a dBV calibration on the chart. This is accomplished by the "insert voltage" method of ANSI S1.10. To calibrate the scale in terms of open circuit microphone output, the method requires "inserting" a known voltage in series with the microphone (with the Sound Source "off"). (The voltage source impedance must be low compared to the microphone impedance.) I found long ago that the ANSI method wouldn't work with a balanced input broadcast type preamp such as the RCA BA -31. I invented a little gadget which I call a "balanced calibrator" to solve this problem, the "Insert V Box" shown in Fig. 1. To make a -60
dBV (1 milli-volt) mark on the chart requires 1 volt into the box. Now if I vary the oscillator frequency and draw a curve with the insert voltage I have what I call a "cal curve," Fig. 7.
The test equipment between microphone and recorder has flat response except for these loading effects on the microphone by the preamp. On some directional microphones, such as the BK -5B, the impedance peak at the low frequency resonance may be four or five times the nominal impedance value. This causes loading of about 3 dB at 50 Hz for the RCA BK-5B/BA-31 combination, and the acoustical response data must be corrected for this deviation. Obviously I could use an op -amp in the preamp input and eliminate microphone loading, but the commercial preamp permits detection of electrical defects in the microphone.
Let's assume that we've calibrated the dB scale of Fig. 6, and drawn the axial response curve, denoted by 0°. The BK 5B has wider and smoother response than many unidirectionals. It is my favorite for all classical or pop music recording. All of the minor "wiggles" or response variations of this excellent microphone are revealed because the smoothness of the Source response exceeds that of the microphone! For everyday work, no corrections for Source response variation need be made to the Fig. 6 curve.
For publication or other purposes requiring accuracy, we need to correct Fig. 6 for Source variations and the "cal" curve. Directional microphone data must be corrected for proximity effect. Certain infidel acousticians would refer to Fig. 4 as the "holy cow" curve, a term that usually refers to calibration curves of commercial speaker sources. These sources have irregular response so that you must constantly compare test curves to the "holy cow," which is a poor testing method.
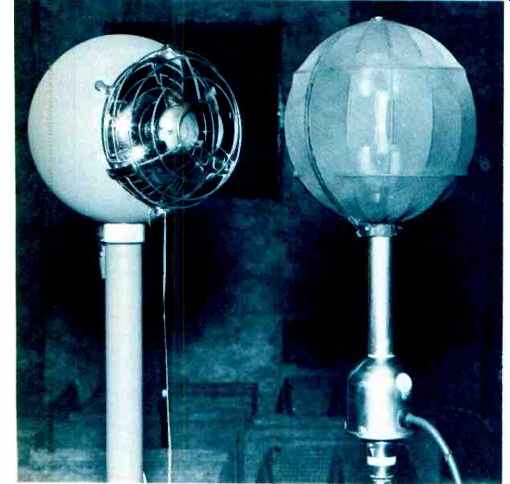
Fig. 4--Small sound source and SPX.
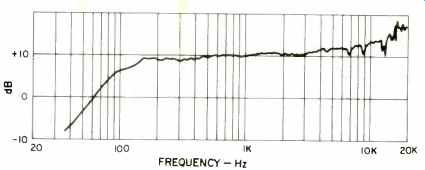
Fig. 5-Calibration of small sound source.
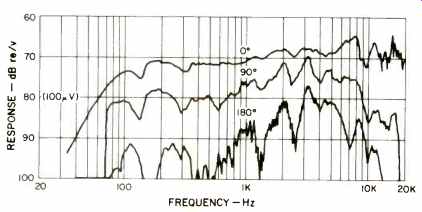
Fig. 6-Chart record of test-BK-SB.
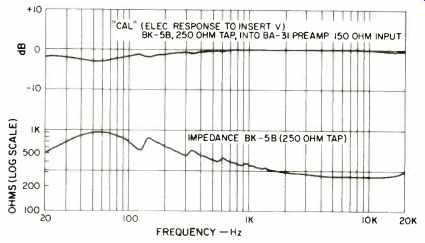
Fig. 7-" Cal" and impedance curves.
Most laboratories do not have custom built sound sources with uniform response, so that various artificial means of "flattening" the SPL versus frequency are employed. One method is to insert a small condenser microphone along side of the microphone being tested. The condenser output is used to regulate the oscillator and speaker output by an AGC circuit resulting in uniform SPL versus frequency at the condenser microphone. This method does not conform to ANSI 51.10 and results in variable errors depending on how much the test microphone disturbs the sound field at the condenser. A better method involves tape recording the condenser mike output with no test microphone in place.
Then the test microphone is substituted for the condenser.
The tape is played and controls the speaker output by AGC action. This method appears to meet ANSI 51.10 but requires periodic re-recording of the tape, plus careful attention to maintenance.
The Source in Fig. 5 was calibrated in 1967. It is current because no significant changes have been observed in the Source since then! The stability and precision of the Source calls for equally precise calibration. Figure 3 shows calibration by our Western Electric 640 -AA microphone. The condenser capsule (the forward most inch of cylinder) is calibrated by the National Bureau of Standards (NBS) and is a Prime Reference Standard Microphone. It is our working standard. Our other 640 -AA, also NBS calibrated, remains in the dessicator, unless we suspect a change in the working standard and need a cross-check. Calibration by 640 -AA involves a preamp, power supply, and potentiometric d.c. meter. Nearly a full day's time is required, so this is not done frequently.
For a quick, every -day calibration check, a secondary standard microphone is used that plugs in place of dynamic or ribbon types. This is the SPX -II Standard Ribbon Velocity Microphone (Fig. 4), developed by A.L. Witchey about 1956.
It was based on the SPX microphone, which was built about 1936 by L.J. Anderson. At that time, there were no good laboratory condenser microphones. The figure -8 pattern of the velocity microphone discriminates against room reflections which cause "wiggles" on speaker response curves. This frequency results in the curves drawn by the SPX-II being smoother than those obtained with an (omnidirectional) laboratory condenser microphone, in real world imperfect anechoic chambers. With a condenser microphone, you frequently go outdoors to obtain a smooth curve. (The velocity microphone is a better choice for testing speakers and "room equalization" adjustments as its discrimination is not unlike binaural hearing. If you want to hear like an omnidirectional condenser, close one ear!) The SPX -II has flat response to 20,000 Hz on or off axis. The 640 -AA, or any one inch condenser, undergoes a change of about 8 dB at 8000 Hz from 0° to 90°. Thus, SPX -II data requires no response correction.
Proximity effect with the velocity microphones close up to sources of spherical waves is easily corrected by RC rolloff equalizing that matches the curves of Fig. 8. You must be in the far field, which means at least twice the source diameter, so your estimate of distance to (equivalent) point source is accurate. Since our Sound Source (diaphragm) diameter is only 2 inches, the far field begins at 4 inches. This permits measurement of the proximity effect of the microphone under test at realistic close-talking distances.
I have applied the corrections for source, preamp loading, and proximity effect to the sample microphone curve of Fig. 6 with the result in Fig. 7. Only the axial response is shown.
The (M) response at low frequencies is essentially flat as shown, for plane wave or distant sources. "M" response is intended for (Music) sources more than 2 feet distant. For close up (voice) the V1 and V2 equalizers compensate for proximity effect.
Directional Pattern
The familiar polar pattern is measured at a single frequency by rotating the microphone and recording on a circular chart. The alternative is to draw frequency response curves at selected angles, such as Fig. 6. This method is easier and emphasizes the importance of uniform frequency response versus angle.
The microphone may be rotated in the horizontal or vertical plane. The horizontal plane is generally selected because of the obvious symmetry of a round diaphragm. The larger the diaphragm, the more high frequency rolloff occurs off-axis. If you have a ribbon 0.060 x 1.0 inch and a 1.0 inch diameter diaphragm, the off-axis response of the ribbon will have much less high frequency loss in the horizontal plane.
But in the vertical plane where the "diaphragms" are similar in dimension, each will have a similar loss. Microphones with physical asymmetry should be tested for both horizontal and vertical directivity. The horizontal pattern is, in most applications, more important than the vertical.
We will use the response versus angle test method in all of our tests. It is not too difficult to translate this mentally into a polar pattern. Look at our example in Fig. 6, in the 500 Hz frequency range, the 0° or front response is the reference and through symmetry, is identical to the 270° response. The 180° response is more than 15 dB down, which is a null or zero response for practical purposes. This is a tricky example: Your mental polar pattern is not a cardioid because the 90° response is more than 6 dB down. It is not a super-cardioid because no rear lobe has developed to accompany the increased "sharpness" of the frontal pattern. It turns out that this is the so-called "uniaxial" characteristic described in a patent by Dr. H.F. Olson. This characteristic provides more reduction of reverberation or noise than a cardioid or super-cardioid.
Using the same mental process, note how the polar pattern becomes poorer than a cardioid at 3000 Hz. Variation of directional pattern with frequency is undesirable and is often observed at high frequencies. Good discrimination at low frequencies is relatively more important. The sound absorption of rooms usually increases with frequency, so that the undesired reverberation and noise are much more intense at lower frequencies.
Impedance Test
The very simple test arrangement of Fig. 10 was used for many years at RCA in the manufacture of ribbon microphones. The a.c. current is generally 10 microamperes, which will not harm any type of microphone. The current remains constant so that
V=IZ=10-SZ
Voltage is the analog of impedance. When Z equals 1000 ohms, V equals 0.01 volts. If Z is 150 ohms, V is 0.0015 volts.
By varying the frequency, the curve of Fig. 7 is obtained. The BK -5B has large magnets, and at low frequencies the exaggerated peak is entirely related to ribbon motional impedance. The curve does not settle down to the nominal 250 ohm value until 5000 Hz! The impedance in this region is attributable to the d.c. resistance of the ribbon (multiplied by a transformer). Before you get upset, recall that microphones should work into unloaded inputs. The " Cal" curve of Fig. 7 shows rather negligible loading even with a mismatch in nominal impedances. This test uses a broadcast preamp, but I obtain equally good results with a Revox recorder and Shure line transformers.
Omnidirectional dynamic microphones generally have a flat impedance curve, and a response doesn't vary with (resistive) loading. A matched load may be used. These remarks also apply to a condenser or any microphone having built-in electronics.
Cardioid dynamics will have an impedance curve similar to the ribbon type, with the resonant peak generally higher in frequency and lower in amplitude. The resonance corresponds to the low acoustical cutoff frequency of either dynamic or ribbon directional microphones.
Phasing
Correct phasing of microphones is of obvious importance. Phase reversals when using similar microphones generally result from user error. If you mix up types, then you should rely on the manufacturer's data for correct corrections.
All microphones should conform to EIA RS -221 but some do not. The standard does not mention 3 -pin XL -type connectors except to require that the plus terminal be marked with a red dot or stripe, but I have never observed this marking on any microphone. The standard also requires the red (or non -black) cable conductor to be a plus, with positive sound pressure.
The test methods suggested in RS -221 are not practical, though I have found the EMT Polarity Tester to be accurate and easy to use. Its operation is shown in Fig. 10. The detector reacts to the polarity of the pulse leading edge.
Hum Sensitivity
In the 1950s an RCA study of broadcast studios revealed that 1 milli-gauss was a reasonable number for the flux density of an ambient 60 Hz magnetic field. Since then, broadcast and professional grade microphones have published Hum Sensitivity Ratings. This rating is the same as Power Sensitivity, except an input of 1 milli-gauss 60 Hz is specified. The rating should be comparable to the equivalent noise input of the preamp. A low noise preamp would have a rating of -125 to -130 dBm for 15 kHz bandwidth. The microphone thermal noise is on the order of -132 dBm, and studio microphones should have -125 to -135 dBm hum sensitivity. Lavalier or hand-held microphones should be -115 to -120 dBm.
I find that microphones for non-professional applications may not have a rating, so I feel that a quantitative test is a waste of time. I will make subjective comparisons with a microphone I know to be good (BK -5B, -130 dBm), using a hum field of approximately 1 gauss. Any microphone that appears to have high hum will be so indicated. This would be an important consideration only if you plan to use the microphone for distant speech or classical music, or for any application in a high hum field.
Wind and "Pop" Sensitivity
There is much confusion concerning these phenomena.
To begin with, I shall quote Dr. Harry Olson, who said to me on more than one occasion that "wind sensitivity is proportional to microphone sensitivity." This means that wind sensitivity, with other things equal, is not a function of the type of transducer element. There is subjective appeal in believing that a fragile ribbon, for instance, is more wind sensitive than a plastic diaphragm. Not so! I have observed high wind sensitivity in microphones of all types. Wind sensitivity is related to the performance of the microphone screens, grilles, and case. A good aerodynamic shape, such as a sphere on the end of a cylinder, encourages non-turbulent flow of air which results in low wind noise. I have also encountered a misconception regarding the mode of noise generation, the sound of wind flowing around trees or houses is not the noise with which we are concerned. That is ordinary airborne sound. Wind noise is generated at the microphone by a steady or " d.c." flow of air (or at least it was before you introduced the microphone.) "Pop" noise is closely related, but it is noise generated at the microphone by a pulse of air from the talker, usually a "p" sound.
In addition to a good aerodynamic shape, a microphone needs wind protection in the form of layers of cloth or open -cell acoustical foam and the wind screen should be as large as possible. A small diameter foam screen is often as effective as a large cloth covered screen. Objective tests of wind sensitivity are difficult. Usually you must swing the microphone in a circle at the end of a boom. Blowers are not suitable because they are not quiet. I have seen a small, easy to use, "pop" generator at one laboratory, but none of these methods is "standard." It is quite easy to subjectively rate microphones for "pop" by reciting "Peter Piper picked..." at close range. "Low" noise is evidenced by the non-existence of "pop." "High" noise causes loss of speech intelligibility and is very objectionable. "Medium" is somewhere in between. Although a performance standard is not really needed, I usually refer to the BK-5B as a standard as it has low wind sensitivity and an integral blast filter (which resists gun shots) plus a large accessory windscreen.
Vibration Sensitivity
Unlike wind noise, vibration sensitivity is primarily related to the mass, and the noise is generated by motion of the case relative to the moving system. A massive diaphragm, such as found in dynamic cardioid microphones, will tend to stand still while the case vibrates, generating high noise. A lightweight ribbon will tend to vibrate with the case, generating low noise.
A secondary mode found in certain microphones involves a bell -like "ringing" of the case or housing. This is generated differently. The vibration case generates airborne sound, which is picked up as ordinary sound by the transducer element. "Ringing" can be quite severe in die cast aluminum housings. In this instance, vibration sensitivity is, like wind noise, proportional to microphone sensitivity. Obviously all types of transducers will pickup the ringing sound equally.
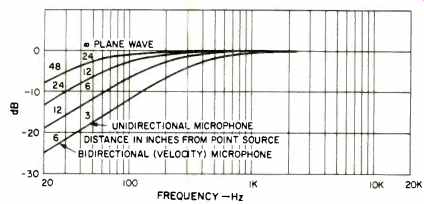
Fig. 8-Inverse of proximity effect.
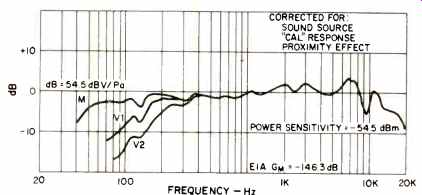
Fig. 9-Frequency response of BK-5B.
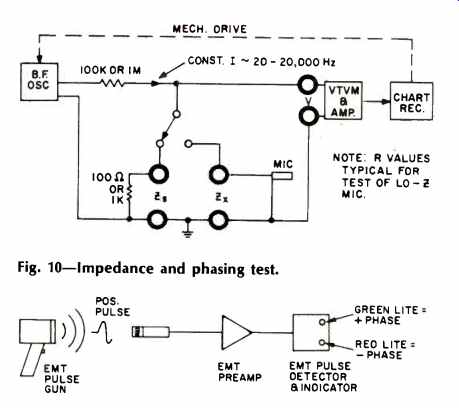
Fig. 10-Impedance and phasing test.
The mass -related or "seismic" type vibration noise can be reduced by cushioning the transducer within the case. The "bell" noise cannot be reduced by cushioning. This noise can be reduced by "detuning," adding mass or stiffness to the case or by adding viscous, damping material to the case.
"Detuning" usually involves expensive tooling changes and is rarely considered. Damping is less expensive and is often a by-product of materials such as silicone compounds used to secure transformers or other parts inside the case.
Vibration sensitivity is another peripheral item where objective testing can be complex and no standards exist. I will therefore perform a subjective test, comparing the test unit to the BK -5B as a standard; I have never tested a microphone with lower vibration sensitivity than the BK -5B.
Distortion
I recall from studies by Olson that dynamic or ribbon microphones have low distortion levels well up past the overload of any known preamp. The margin is such that a 10 or 20 dB attenuator on the microphone does not change this conclusion. Microphones incorporating electronic amplifiers, such as condensers, have a clipping level that is frequently below preamp overload, depending on gain factors.
The only way to generate the required pure tones at 110 to 130 dB SPL is with a resonant pipe. This is not worth the effort, because the voice can generate peaks up to 130 dB at close distance. Peak clipping is easily observed on a scope.
Knowing the acoustic sensitivity, the clipping SPL can be calculated. If your application is rock music, then a clipping (peak) level of 130 dB is desirable. For classical music, 120 dB is satisfactory.
Biomechanics
This is, I believe, a new term which refers to human factors involved in the physical operation of tools or machines.
It is currently being applied as a science by Ingersoll-Rand in design of hand tools, and they have published some results which can be applied to microphone evaluation. These concern the motions and positions of the fingers, hand, wrist, and arms. Microphones that "feel" awkward to use probably violate some of the rules of biomechanics. As an example, the fork mount on our favorite BK -5B microphone is so awkward to use that it will be our standard for "poor" biomechanics. Microphones that are easy to use and have a good "feel factor" will be rated "good." The "fair" rating will apply to others.
Listening Test--Audio Quality
Listening tests of microphones are best performed by making an A-B test, comparing the unit on test to a reference microphone. The reference microphone, theoretically, is an arbitrary choice, but I will choose a high quality unit of similar type that is familiar to me. (A comparison of an omnidirectional to a cardioid type is not valid, for instance.) You may object to my choice of an RCA broadcast microphone, for example. There might be a large difference in price, it is sold primarily to broadcast stations and practically impossible for an audiophile to obtain. However, if I choose a well-known microphone, my experience is that if the test unit is rated poorer than the reference, people will conclude I am "selling" the reference microphone. I can more easily maintain an unbiased posture by choice of a reference that is not generally available to the market. If I always use the same reference, the ratings between microphones can be accurately compared, just the same as hum, wind, and vibration ratings.
Quality and Durability
This is the most subjective rating. You must rely on my judgment as an expert. The "standards" will be existing samples or mental images of microphones tested in the past. If I suspect fragility, I may drop the microphone or pull on the cord. Ratings of poor, fair, and good will be assigned.
Conclusion I have described how we will test microphones and how to interpret our ratings. Sufficient tutorial material is included to enable the audiophile to sort out the many performance factors and make a more intelligent choice of a microphone for a particular application. The increasing sophistication, cost, and complexity of home audio equipment will result in wider use of professional grade microphones. The user will therefore require more knowledge and technical information about microphones, and we hope that such articles and tests as these will provide such knowledge.
Also see:
Part 2: The Compleat Microphone Evaluation--An Update (Sept. 1978)
An Inexpensive Microphone (The Workbench) (May 1973)
(Audio magazine, April 1977 )
= = = =