

by ROBERT F. HERROLD
Robert F. Herrold is working on a book about microphones, and this article is adapted from portions of his manuscript. He is currently employed as Product Manage-, Microphones by Audio-Technica in Stow, Ohio.
A microphone is a transducer, a device that converts one form of energy into another; in the case of a microphone, sound energy is converted into electrical energy. Although all microphones are transducers, the various types of microphones convert energy in different ways.
All microphones require a means to "gather" sound, to be able to reproduce it. Moving-coil or dynamic microphones gather sound by means of a movable diaphragm. Attached to the diaphragm is a coil of wire typically made of copper, aptly named a voice-coil, which surrounds a permanent magnet.
Elementary physics tells us that when a coil of wire moves in a magnetic field, an electrical voltage will be induced in the coil. When sound energy hits the diaphragm of the microphone, it responds sympathetically along with the attached voice-coil, c eating an output voltage (see Fig. 1).
Because the output voltage of the microphone is very small, it requires amplification to be usable. The amplified voltage signal will eve-dually be converted back into sound energy via another type of transducer, either a loudspeaker or headphones. With the exception of the telephone mike, the moving-coil or dynamic microphone is probably the most widely used today. It is extremely rugged, and its output impedance is low. Impedance will be discussed later. (The voice-coil leads shown in Fig. 1 have been illustrated simply, for convenience Typically, these fragile leads are internally dressed to keep them from being accidentally broken.)
Electret Condenser Microphones
The electret condenser microphone also reproduces sound via a movable diaphragm; however, there is nothing attached to the diaphragm as with the moving-coil microphone.
The term "condenser" may be confusing unless you know that it is merely another term for "capacitor." Electrical engineers tend to use "capacitor," while microphone engineers and users generally say "condenser." An electronic capacitor is a device that allows an alternating voltage or signal to pass through it. Due to its basic nature, the capacitor will not allow a d.c. (direct, non-alternating) voltage to pass through it. The electronic capacitor has two fixed, internal plates (as shown in Fig. 2).
The electret condenser microphone's element is similar to an electronic capacitor, but it incorporates one fixed plate and one moving plate (the "metallized surface" shown in Fig. 3). Sound hitting the moving diaphragm causes an output signal to be generated. For the electret condense' microphone, one other requirement must be met in order to successfully generate an output signal--a d.c. voltage potential, known as a bias voltage, between the two plates. The bias voltage is referred to as a permanent electret charge. (The term "electret" implies a permanent-charge situation.) In most current electret designs, the electret charge is placed in the fixed plate or back plate.
The output impedance of the electret condenser microphone is so high as to be unusable. To transform this ultra-high impedance into a usable impedance, an electronic circuit called an impedance converter is incorporated inside the microphone. The impedance converter consists of a device called a field-effect transistor, or FET, which requires a source of power to operate, just as an ordinary transistor does. The source of power can be an internal battery or an external phantom power source, depending on the design of the microphone. Phantom-source microphones are typically more expensive than their battery-powered, electret condenser counterparts.
The true (non-electret) condenser microphone works in the same fashion as the electret condenser microphone, but it has no permanent charge between the two plates. The true condenser requires a special, internal, voltage-boosting circuit powered by an internal battery or an external power source. The voltage boost is required to obtain the proper bias voltage between the two plates.
Depending on the design, the electret condenser microphone can function on battery voltages ranging from 1.1 to 9 V. Requirements for phantom power voltages may range from 9 to 48 V. Modern-day, true condenser microphones use 48 V of external (phantom) power, and utilize a built-in, voltage-booster circuit as mentioned above. Older condenser mikes required an external power source of 200 V.
Condenser-type microphones typically yield the widest frequency response and the highest output sensitivity of any low-impedance microphone type.
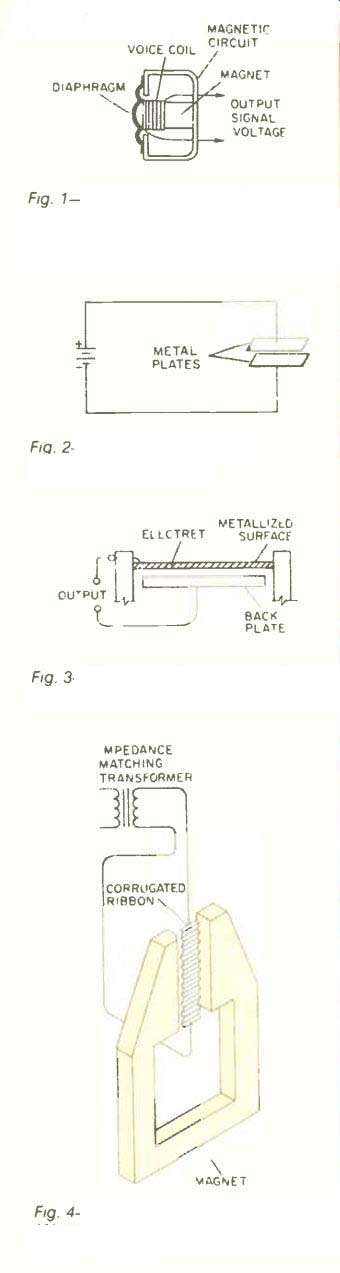
Fig. 1--Moving-coil or dynamic microphone. (Alter Martin Clifford, Microphones-How
They Work & How to Use Them.)
Fig. 2--Electronic capacitor. (After Clifford.)
Fig. 3-Electret condenser microphone. (After John Eargle, Sound Recording.)
Fig. 4-Dynamic ribbon microphone. (After John M. Woram, The Recording Studio Handbook.)
Dynamic Ribbon Microphones
The ribbon microphone (Fig. 4) is another type of dynamic microphone. Also called a velocity microphone, i; works on the same principle as the moving-coil or dynamic. However, instead of utilizing a diaphragm and attached voice-coil, it uses a combination ribbon diaphragm/voice-coil which is pleated (or corrugated) to give it strength and stability. The metallic ribbon moves in the magnetic field of the permanent magnets in response to sound pressure; this results in a voltage generated along the length of the ribbon, the output signal. The pleated ribbon is susceptible to permanent stretching if a sudden blast of air hits it, altering the sound of the microphone. (Obviously, it is not a good idea to blow into such a microphone.) The output impedance of the dynamic ribbon microphone is low.
PZM Microphones
The PZM (or boundary) is a special microphone for special applications; "PZ" stands for pressure zone and "M" denotes microphone. The pressure zone is a constant area of pressure that exists within a few thousandths of an inch of a flat, hard surface. The PZM utilizes a small, omnidirectional or unidirectional electret condenser transducer in a housing suitable for mounting on a flat surface. The output impedance of the PZM is low.
Line (Shotgun) Microphones
The line microphone (Fig. 5), or shotgun, as it is often called, can use a moving-coil, a condenser, or electret condenser transducer. The best performance from the shotgun is achieved by using a condenser, because this type of transducer yields higher sensitivity and better polar and frequency response than the others. Condenser-type units can also be smaller in diameter and lighter in weight. (Sensitivity, frequency response, polar response, and impedance will be covered later.) The output impedance of the line microphone is low.
The line opening along the front portion of the microphone leads inside to a very narrow slot, or line, in a small-diameter tube. Sound enters the line opening and travels down the tube to the diaphragm. At frequencies that have wavelengths shorter than a certain selected wavelength, sound entering the line is cancelled except for sound approaching almost entirely along the axis of the microphone. Maximum cancellation occurs at 90°. This is why it is referred to as a shotgun microphone: It tends to pick up sound only from the direction in which it is pointed.
At frequencies in which the wavelength is longer, the line mike no longer functions so selectively, and the pickup pattern tends towards more uniformity with angle. Therefore, a rear entrance is added to make the line microphone into a cardioid (a heart-shaped directional pattern) at lower frequencies, where the line no longer functions. Because the shotgun microphone is very directional, it can be used to pick up sound at fairly long distances. It is often used to pick up dialog in television broadcasts and in the movies where it may not appear on camera.
Contact Microphones
The contact microphone is used to pick up the sounds of a guitar, for instance, by attaching it directly on the surface of the instrument. The contact microphone uses a piezoelectric transducer, two small squares of ceramic material permanently bonded to either side of a thin piece of metal, like a sandwich. The ceramic material contains a permanent electrical charge (somewhat like an electret condenser). The output impedance of the contact microphone is high.
Figure 6 illustrates a piezoelectric microphone transducer. In contact versions, the piezo sandwich is made so rigid that it will not respond to sound waves in the air. It must be physically attached to a vibrating surface, such as the sounding board of a guitar. The sound energy coming from the board causes the sandwich to flex. The flexing action causes an output voltage to be generated across the output leads of the device.
Wireless Microphones
A wireless microphone is so named because the microphone cable has been eliminated. It often uses a moving-coil or electret condenser microphone, though it could be used with other types as well. These microphones generate an output voltage in a typical fashion, but how does this signal reach the electronic input without a cable? The microphone being used has built into it, or plugs into, a small radio transmitter. The transmitted signal is received by a radio receiver placed somewhere in the vicinity of the microphone/transmitter.
As one might expect, wireless microphones cost more than regular types, and some cost thousands of dollars. A good rule of thumb is to multiply the cost of a regular microphone by a factor of at least 10 to determine the price of the wireless version. Most wireless microphones are used by TV or stage performers who need to be very mobile. Obviously, when a performer must execute a rapid dance number, for example, a microphone cord would get in the way.
Fig. 5--Line (shotgun) microphone. (After Alec Nisbett, The Use of Microphones.)
Fig. 6--Piezoelectric microphone. (After Clifford.)
Fig. 7--Production limits of frequency response.
Fig. 8--Three-pin male cable connector.
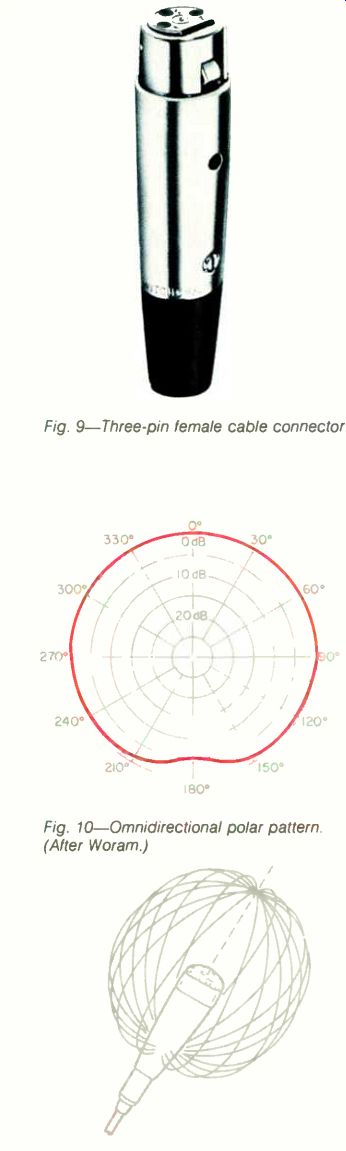
Fig. 9--Three-pin female cable connector.
Fig. 10--Omnidirectional polar pattern. (After Woram.)
Fig. 11--Three-dimensional representation of omnidirectional polar pattern. (After Woram.)
Frequency Response
Frequency response is a familiar term to most people, especially those who own high-fidelity equipment. Most of us know that the range of frequency response a human can supposedly hear is from 20 Hz to 20 kHz. In reality, the average adult cannot hear the extremes of the audio spectrum. Also, I have yet to discover a loudspeaker system capable of reproducing 20 Hz, though it is quite easy for a tweeter to reproduce 20 kHz.
Of the many types of microphones available, few offer flat frequency response. If a microphone has a wide range and flat frequency response, it will obviously be capable of faithfully reproducing sound. But such a response is usually available only in units costing many hundreds of dollars. For that matter, wide-range response is not always desired.
Difficult as it is to design a microphone with a flat and wide frequency response range, it is even more challenging to manufacture quantities of microphones of a given design without individual variations, from one microphone to another, in frequency response. Manufacturers develop what are called production limits, an example of which is shown in Fig. 7.
Production limits allow for a controlled amount of variation from unit to unit. The more expensive the microphone, the tighter the limits (or tolerance). As an example, a microphone costing $500 or more would probably have limits that only vary by 0.5 to 1 dB. Microphones costing $200 to $400 might have limits that vary by 1 to 2 dB. Microphones costing $100 to $200 might have limits that vary by 2 to 3 dB, and very inexpensive microphones might not have any limits, to keep production costs down. (These numbers are not meant to be construed as gospel, of course.) The likelihood of finding two microphones with exactly the same frequency response is about the same as finding two identical snowflakes; however, minor variations in frequency response are undetectable even to the trained ear.
The central curve of Fig. 7 is the curve of the microphone. The top curve is the upper limit of frequency response; the bottom curve is the lower limit. The reference point for production limits is usually 1 kHz because microphone frequency response is normally stable in this area, whereas there tends to be some variation at very low and very high frequencies.
The production limits for this microphone vary by approximately ± 2 dB.
Figure 7 allows us to determine several things about this particular microphone. It does not have a flat frequency response, nor does it have a frequency response of 20 Hz to 20 kHz.
As the frequency response is usually thought of as the points at which the curve is 3 dB down from flat, it can be seen that this microphone's range is from 50 Hz to approximately 15 kHz.
"Flat" is determined here with reference to the 1-kHz stable area of the microphone curve.
Sometimes a frequency response range for a microphone will be given in a manufacturer's literature, but no curve will be shown. In such cases it is not safe to assume, for instance, that the stated response is 3 dB down at the end points; it may be 3 dB up. You will be most likely to encounter this problem when dealing with very inexpensive microphones.
Most microphones that are designed to reproduce the entire audio spectrum are expensive, calibrated laboratory types, used for highly accurate acoustical measurements. The majority of microphones today do not have a flat, wide-range frequency response, for a good reason. Microphone applications vary widely and require different types of response curves to meet them. This is why frequency response curves are so important; we may incorrectly assume that the frequency response stated by the manufacturer is flat, just as we may erroneously assume the frequency response to be 3 dB down at the extremes.
Many microphone users prefer a rising high-frequency response; however, microphones exist which have responses that are flat, rising, falling, or rolled off. Typically, flat microphones and those with a rising high-end are used in recording. Microphones with rising response and low-end roll-off are preferred for up-close vocals or speaking. Microphones with a rising high-end are also liked in live applications for picking up cymbals, brass, etc.
Impedance
Impedance means something that is a hindrance. In audio usage, impedance hinders the flow of an alternating current in an electronic circuit. The unit of measurement used for impedance is the ohm.
Technically, impedance is made up of two basic components, the first of which is resistance. A resistive electronic device is called a resistor. The second component of impedance is reactance, which can consist of a capacitor or an inductor (coil). (Usually a small coil of wire is used in an electronic circuit.) The value of a resistor remains fixed unless it is subjected to excessive current flow, in which case it could be damaged. But the value of a capacitor or inductor varies with frequency. The impedance of a microphone is normally measured at a single frequency and is considered constant or resistive in nature. However, if one were to measure the microphone impedance at different frequencies, there would be a significant change in value.
The sum of the values of the resistive and reactive components at a given frequency determines the total value of the impedance of the microphone. This is the value stated on the microphone's specification sheet.
There are two basic microphone impedance classifications in wide use today, low impedance (Lo-Z) and high impedance (Hi-Z). It is important to use Lo-Z microphones with Lo-Z equipment and Hi-Z microphones with Hi-Z components. But what if you don't know what the input impedance of your equipment is? Simply plug in the microphone and find out if it will work.
You don't have to worry about doing any damage, either to the microphone or to other stereo components. If you plug a Lo-Z microphone into a Hi-Z input, the resulting sound output will be very weak and you will have great difficulty in speaking or singing loudly enough to be heard. If you plug a Hi-Z microphone into a Lo-Z input, the sound will be loud, probably distorted.
It will also have an overabundance of bass, and high-frequency response will be totally lacking. Obviously, if you plug in the microphone and everything comes out sounding good enough and loud enough, the impedance match is correct.
Low-impedance microphones used in pro and semi-pro recording normally are wired in a three-conductor, balanced-line configuration to reduce noise pickup and hence permit the use of longer cables. A three-pin male audio connector (Fig. 8) at the output end of the cable mates with a three-pin female panel connector at the equipment's input. (A three-pin female connector is shown in Fig. 9.)
There are some Lo-Z microphones in use today that have a 1/4-inch phone-plug output-cable connector; these are usually inexpensive types for use with cassette recorders. The 1/4-inch phone plug mates with a 1/4-inch phone jack on the recorder.
Some cassette recorders have miniature phone-jack inputs. Adaptors are readily available to convert a standard 1/4-inch phone plug into a mini-phone plug. High-impedance microphones also use a 1/4-inch phone plug on the equipment end of the microphone cable, which would mate with a 1/4-inch phone-jack input connector.
Examples of Lo-Z equipment using three-pin input connectors are more expensive reel-to-reel tape recorders and microphone mixing consoles (mixers). Examples of Hi-Z equipment using 1/4-inch phone-jack input connectors are inexpensive mixers, guitar amplifiers, and older cassette decks and open-reel tape recorders. Some cassette decks are made to work properly with both impedance types by using an automatic, impedance-compensating network.
Fig. 12--Head diffraction, omnidirectional microphone.
Fig. 13-High-frequency roll-off due to case diffraction, omnidirectional microphone.
Fig 14--Cardioid polar pattern. (After Woram.)
Fig. 15-Three-dimensional representation of cardioid polar pattern. (After Woram.)
Microphone Sensitivity
Microphone sensitivity (or output level) is the measure of the output voltage of a microphone which is subjected to a known amount of audible sound pressure level (SPL) input. For the sake of uniformity, all manufacturers have an accepted sound pressure standard they use to specify the sensitivity of a microphone. This makes it easy to compare models from different manufacturers. The standard sound pressure level used is 94 dB. A typical sensitivity specification for a low-impedance dynamic microphone might be: -56 dB re: 1 mW/10 dynes/cm^2. (1)
At first glance this appears to be written in Greek, but upon closer inspection, it becomes obvious that most of the terms used are standard abbreviations. To understand what the above specification is saying, each term needs to be looked at individually.
First, -56 is a negative number which implies that it is less than another, more positive number. (More will be said about this in a moment.) The abbreviation dB can be recognized as the decibel; "re" is an abbreviation for the term "referenced to." Continuing, mW stands for the term milliwatt. The prefix milli means 1/1,000; watt is a unit of power. Therefore, 1 mW is 1/1,000 watt-not much when compared to the power utilized by a light bulb. The next term, dyne, is a metric unit of force much smaller than an ounce. Last, cm2 stands for centimeter squared, or square centimeter. There are approximately 2.5 centimeters to an inch.
Dynes/cm^2 is a short way to say dynes per square centimeter. By definition, a force per given area is pressure, so 10 dynes/cm^2 is the amount of pressure that is exerted upon the diaphragm of the microphone.
It can be pointed out here that 10 dynes/cm^2 is equivalent to 94 dB SPL, which is the standard pressure for measuring microphone sensitivity.
Plainly stated, equation (1) says that the microphone in question has a sensitivity that is 56 dB less than the arbitrarily agreed-upon 0-dB reference, which is 1 milliwatt per 10 dynes per square centimeter.
The pressure (10 dynes/cm^2) can appear on specification sheets in several different forms, as follows: 10 dynes/cm2 = 10 microbars
= 1 Pascal = 1 Newton/meter^2
= 94 dB SPL. (2)
One could replace 10 dynes/cm2 in equation (1) with any of these other terms and still have the same equation.
Equation (1) can be further abbreviated by writing it as-56 dBm. Many specifications show the sensitivity in this abbreviated form, where "m" stands for 1 mW/10 dynes/cm2 and automatically implies the milliwatt reference.
If a microphone is 6 dB more sensitive, say, than the one described in equation (1), its specification would be written-50 dBm. Therefore, the less negative the sensitivity number, the more sensitive the microphone. Dynamic microphones normally fall in the sensitivity range of -50 to -65 dBm. Condenser types generally fall in the -35 to -55 dBm range.
So far, only the sensitivity of low-impedance microphones has been discussed. The sensitivity specification for high-impedance microphones is stated differently, but this does not present a problem.
A typical specification for a high-impedance microphone might resemble: -75 dB re: 1 V/dyne/cm^2 (3)
Looking at equation (3), it is seen that the sensitivity number is negative, as before, but it is obvious that the reference has changed. In lieu of 1 mW is 1 V, where V stands for volt.
Also, 10 dynes/cm^2 has now become 1 dyne/cm^2, a change by a factor of 10 in the force on the diaphragm. A factor-of-10 change means a 20-decibel change.
Therefore: 1 dyne/cm^2 = 1 microbar
= 0.1 Pascal = 0.1 Newton/meter^2
= 74 dB SPL. (4)
When testing high-impedance microphones, manufacturers still use the standard 94 dB SPL, but they mathematically adjust the resulting sensitivity downward by a factor of 10, or 20 dB. Equation (3) can also be simplified by rewriting it as -75 dBV, where V stands for 1 dyne/cm^2 and automatically implies a voltage reference.
At this point, one might ask a very logical question: "When should I use a high-sensitivity microphone in preference to a low-sensitivity microphone?" Low or high sensitivity is not a function of whether the microphone has low or high impedance, so I'll discuss sensitivity in terms of low-impedance microphones, the type used in the majority of applications today.
High-sensitivity microphones are preferred in those applications in which the microphone must be placed at some great distance from the source of sound, such as on a movie or TV set, or when recording an orchestra, recording a choir, or picking up a play.
High sensitivity is appropriate for these applications, since it affords the best signal-to-noise ratio by allowing mixing-console and amplifier gain (volume) to be set at a minimum. The lower the gain settings on electronic devices, the less internal self-noise is amplified, thus minimizing hum, hiss and other electrical or electronic noises.
High sensitivity is a drawback when a microphone is going to be used very close to the source of sound, such as when close-miking a trumpet, a rock vocal, a kick drum, or an amplified instrument. A high-sensitivity microphone puts out considerably more voltage than one of lesser sensitivity. Indeed, when exposed to a loud sound source, such a microphone puts out a surprising amount of voltage-enough to overload the input of a mixing console or tape recorder.
Input overload means that the maximum input voltage rating of the tape recorder, mixer, amplifier, or other electronic device has been exceeded, resulting in a very noticeably distorted sound. People are often quick to place the blame for this on the microphone, but usually it is the input of associated equipment that is distorting, not the microphone.
When a signal greatly exceeds the maximum input voltage of the electronics, there will be flat spots in the most positive and the most negative portions of the signal; these portions will not pass through the equipment and so will be lost. Such a signal is referred to as a square wave; it results in sound that is very distorted to the ear.
A microphone with lower sensitivity will often correct this situation. If not, an input attenuator (pad) should be used. These devices are available with fixed values of 10 or 15 dB, or with 10-, 20- and 30-dB steps.
Although there is no specific point at which a microphone's sensitivity can be classified as "high" versus "low," I feel that microphones having an output sensitivity in the range of-54 to-35 dBm, or greater, can be considered to have high output sensitivity. Those microphones in the range of -55 to -75 dBm, or less, can be considered to be of low sensitivity.
=========
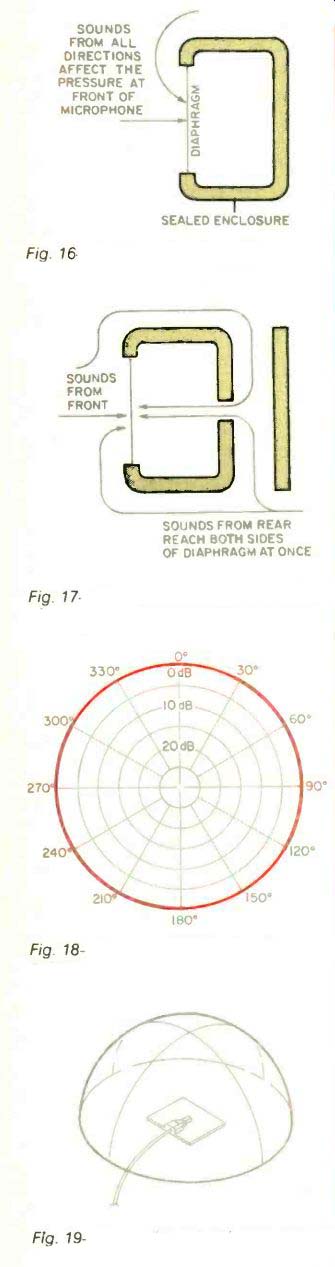
Fig. 16-Omnidirectional microphone capsule. (After Woram.)
Fig. 17-Cardioid microphone capsule. (After Woram.)
Fig. 18-Boundary (PZM) microphone polar pattern.
Fig. 19-Three-dimensional representation of boundary microphone's polar pattern.
========
Though the dynamic microphone will seldom distort, there are situations in which the microphone itself can cause distortion. Well-designed condenser types will not distort unless the sound pressure they are exposed to exceeds 135 to 140 dB. Some of these microphones have switchable internal pads that will add another 10 to 15 dB of headroom before distortion occurs.
The electret condenser that is internally powered with a 1.5-V battery will typically distort if SPLs of 125 to 130 dB are exceeded. This is equivalent to a rather loud vocal, so the problem is not cause for undue alarm.
At this point it might be useful to summarize some of the main points made here about microphone sensitivity. When two microphones are subjected to the same sound input, the one that generates the largest output voltage is said to have the greatest sensitivity. For low-impedance microphones, this is expressed in decibels relative to 1 milliwatt; for high-impedance units it is given in decibels relative to 1 volt. High-sensitivity microphones are good to use for pickup of distant sounds, while low-sensitivity models are good for close-up sounds.
All microphones, but particularly those with high sensitivity, can overload equipment, causing distortion; this can be eliminated by using an attenuator (pad). Low-voltage condenser microphones can also cause distortion when exposed to very loud sounds.
Polar Response (Directionality)
Most people have difficulty visualizing and understanding polar patterns because they are normally depicted in a two-dimensional form on paper. In reality, they are three-dimensional.
The three-dimensional aspect of polar response can best be explained by considering the simplest pattern, the omnidirectional. As its name implies, the omnidirectional microphone picks up sound from all directions. This is illustrated in Figs. 10 and 11.
Regardless of where a sound source is located along the circle shown in Fig. 10, an omnidirectional microphone at the center "hears" the sound just as though it were coming from directly in front. In other words, the omni microphone picks up sound from all directions equally well. Other microphone types that do not have this capability will be discussed later.
If Fig. 10 were made to be three-dimensional, it would take on the appearance of a balloon as shown in Fig. 11. If a person were to stand anywhere on the surface of the balloon and talk, it would have the same effect as if he were standing directly in front of the microphone.
The omnidirectional microphone described so far is actually an idealized model. In reality, omnidirectional microphones exhibit some directionality (the tendency to be other than omnidirectional) at higher frequencies, due to their shape. To be truly omni, the microphone housing must be cylindrical (tubular) and measure V2 inch or less in diameter.
With a reasonable shape for an omni microphone, the handle is cylindrical but the head is not, and it is larger in diameter than the handle. High frequencies have difficulty trying to get around the head when approaching from the rear. Figure 12 shows high frequencies diffracting off the head, thus causing the sound intensity at these frequencies to be reduced. Lower frequencies have longer wavelengths and are able to turn corners.
In Fig. 10, the perimeter of the circle represents the ideal omni. The inner, curved line represents loss of high frequencies due to the aforementioned "head" or case diffraction.
The concept of polar patterns still may not be entirely clear. You may be asking, "Exactly what frequencies does the inner curve represent?" If the microphone were truly an omni, the outer circle would represent all frequencies. But because the high-frequency loss becomes greater as the frequency increases, the inner curve shown it Fig. 10 can only be true for a single frequency. From the standpoint of the high-frequency loss concept, however, the curve serves its purpose.
Figure 13 should help to clarify this concept. The top curve shows the on-axis (0°) response of the microphone, and the others show high-frequency roll-off due to diffraction off the case.
As previously mentioned, the roll-off becomes more pronounced as frequency increases.
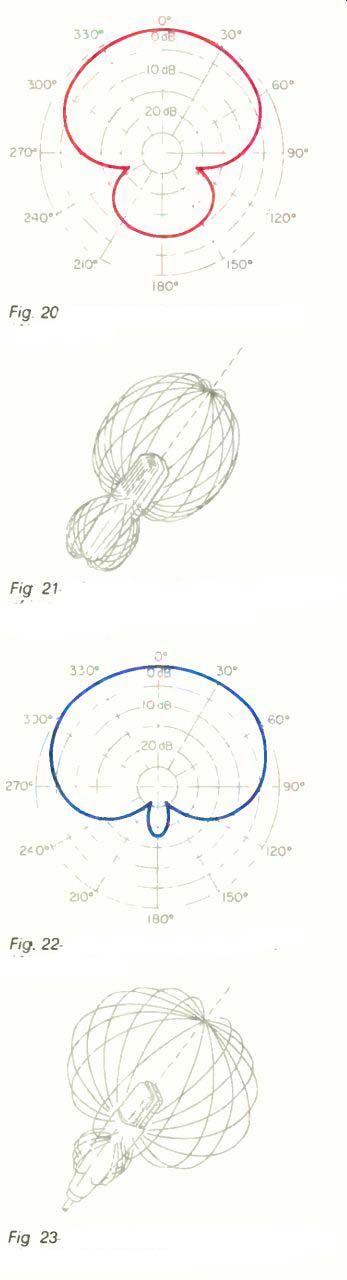
Fig. 20--Hypercardioid polar pattern. (After Woram.)
Fig 21--Three-dimensional representation of hypercardioid polar pattern. (After Woram.)
Fig. 22-Supercardioid polar pattern. (Alter Woram.)
Fig 23--Three-dimensional representation of supercardioid polar pattern.
From a consideration of the omnidirectional microphone's polar pattern, we can more easily understand the polar pattern of the most widely used microphone today, the cardioid. The term unidirectional is often used in place of cardioid, even though it is a misnomer. Unidirectional implies only one direction, and such a device does not yet exist. The word cardioid means heart-shaped.
Figure 14 shows a cardioid (heart-shaped) line indicating how the microphone actually responds at the different angles. In comparison, the outer perimeter of the circle represents what an omni microphone response would be under the same conditions, if it were to replace the cardioid. Figure 15 shows that the cardioid polar pattern, in three-dimensional form, has somewhat the appearance of an apple.
At the 90° and 270° positions in Fig. 14, it will be noticed that the output of the cardioid is lower than the omni. At these positions, the output of the cardioid is half that of the omni, or 6 dB less.
At 180°, the output of the cardioid microphone is at its minimum (maximum rejection of unwanted sound occurs), possibly one-tenth or less of the output of an omni.
Fig. 16 shows an omnidirectional microphone capsule exposed to sounds converging upon it from various directions. Notice that all sound must converge to the front of the microphone, at the diaphragm. This is why its polar pattern is spherical.
Figure 17 shows a cardioid microphone capsule exposed to sounds arriving from various directions. Notice that sound can converge directly on the front of the diaphragm and indirectly on the rear of the diaphragm, through the rear opening.
The front and rear openings of a cardioid microphone are acoustically balanced for several reasons: Sound approaching directly from the front of the microphone hits the diaphragm first and produces sound output from the microphone. Sound also enters the rear opening, but it is (purposely) slightly delayed in order to be out of phase with the sound entering from the front. This delayed rear sound also produces a sound output from the microphone.
Sound approaching the microphone from the sides arrives first at the front of the diaphragm, but the sound entering the rear openings arrives at the rear of the diaphragm just a little later, thus reducing the sound output by half (-6 dB). Sound approaching from the rear of the microphone enters the rear opening first. It is delayed (by an internal acoustical-delay mechanism) so that it arrives at the rear of the diaphragm at the same time as the sound reaches the front of the diaphragm, resulting in little or no output from the microphone due to cancellation.
Because the cardioid microphone discriminates against sound approaching it from the rear, a big benefit is derived: The reduction of feedback.
Feedback is a howl or squeal that can occur when a microphone is in the same room with the loudspeaker that is reproducing the sound. If the amplifier is turned up too high, the microphone can "hear" itself in the loudspeaker.
Suddenly, a point is reached at which the original signal from the microphone is amplified rapidly over and over again, resulting in a sustained howl or squeal.
The cardioid microphone provides a significant reduction in feedback and background noise compared to an omni microphone. In addition, a cardioid has two other distinct advantages over the omni. The distance from the sound source to the cardioid can be twice that of the omni and still provide the same quality of sound pickup.
When used at the same distance from the sound source as the omni, the cardioid will reduce background ambience by two-thirds.
Other types of polar patterns exist. Figures 18 and 19 show a hemispherical polar pattern associated with boundary, or PZM, microphones. Figures 20 and 21 depict a hypercardioid pattern associated with certain ribbon and condenser-type microphones made for particular applications. In Figs. 22 and 23, a supercardioid pattern is shown. This is associated with certain dynamic and condenser microphone types used for special applications. Figures 24 and 25 show a bidirectional or figure-eight polar pattern, which is most often associated with ribbon microphones. Figures 26 and 27 depict the polar pattern of a shotgun (line) microphone.
Because the line microphone is a significantly different type, it is appropriate to give a more detailed explanation. The line or shotgun microphone is extremely directional at high frequencies (typically, above 1 kHz) and hypercardioid at frequencies below 1 kHz (though there is no sharp transition at 1 kHz from hypercardioid to line). Therefore, at low frequencies, refer to the hypercardioid polar pattern of Figs. 20 and 21, and for high frequencies refer to Figs. 26 and 27.
At high frequencies, the shotgun microphone will act like a flashlight, in that you have to point it at the sound source to pick it up well. Keep in mind that the "lobe" size of Fig. 26 varies with frequency. It will be larger at 1 kHz than it will be at 10 kHz.
Properly used, polar pattern information can provide the user a tool with which to build an entire sound system for a church, auditorium, meeting room, etc. Or it can be used to design a recording or broadcast studio. Proper understanding of polar characteristics can aid in reducing feedback and ambient noise, which will make for a much higher quality sound pickup and reproduction.
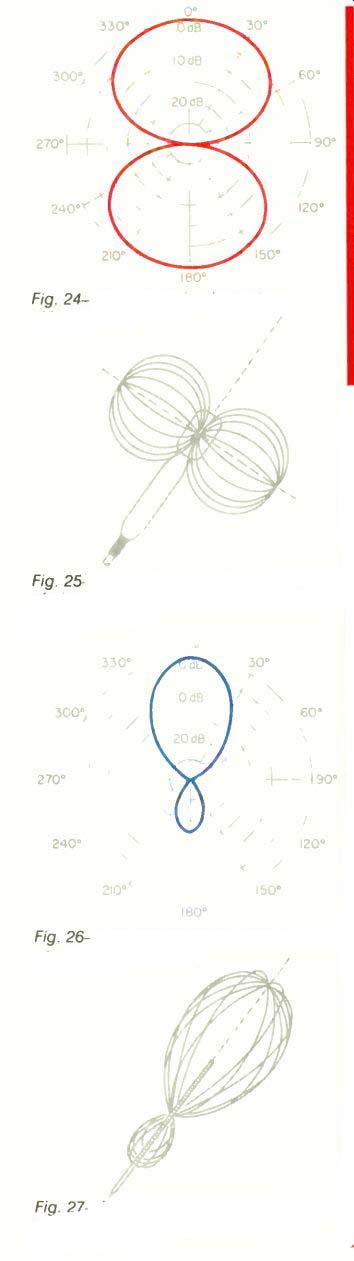
Fig. 24-Bidirectional polar pattern. (After Woram.)
Fig. 25-Three-dimensional representation of bidirectional polar pattern. (After Woram.)
Fig. 26-Line (shotgun) microphone polar pattern. (After Woram.)
Fig. 27-Three-dimensional representation of line microphone's polar pattern. (After Woram.)
(Audio magazine, Apr. 1985)
Also see:
MICROPHONES--Quo Vadis? (Apr. 1972)
A Microphone Primer: Basic Construction, Performance, and Applications--Part 1 (Dec. 1972)
A Microphone Primer: Conclusion (Feb. 1973)
Mike Technique and Sound Effects (Dec. 1974)
Electro-Voice microphones (Jan. 1973)
= = = =