by D.A. Kerr
MOST HEADSETS for use with modern music systems have a nominal impedance of 8 ohms, and most modern stereophonic amplifiers include circuitry to drive such headsets. But many high-quality headsets, such as those intended for professional use, have much higher nominal impedance, typically 600 ohms. The same is true of many representative high quality headsets, including the AKG (Philips) K-180 and Beyer (Revox) DT302 at 600 ohms, Telefunken TH-28 at 400 ohms, Koss Pro/4AA at 250 ohms, Lafayette F-600 and Ercona D-42 at 200 ohms, and Sennheiser HD414 at 2000 ohms.
The audiophile who has two or more headsets of different rated impedances may be at a loss to know how to accommodate them to his amplifier. Fortunately, a simple circuit modification may be easily made to most amplifiers to allow headsets of different impedances to be used interchangeably with comparable performance. No impedance selector switch is required, and the circuit delivers equal audio power to either headset assuming of course, that they are of comparable efficiencies.
Such an arrangement may at first seem paradoxical: if the circuit matches the impedance of one type of headset, it certainly cannot match the other. But impedance matching, in the conventional sense, is not used in the normal headset-driving circuit.
The tiny amount of power required to drive a headset, typically less than one milliwatt, is many thousand times less than a power amplifier would deliver into a truly matched load.
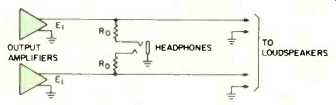
Fig. 1A-Typical circuit for driving stereo headphones.
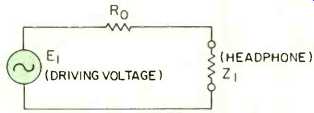
Fig. 1B-Equivalent circuit (one side only).
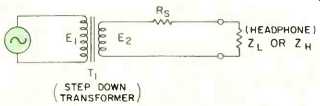
Fig. 2-Basic dual-impedance head-phone circuit.
This is because in modern audio power amplifiers the load (loudspeaker) is not matched to the internal impedance of the output stage.
Typically the source impedance of the output stage is many times less than the rated load impedance. This produces presently accepted values of damping factor and, for modern amplifier circuits, is consistent with low distortion operation.
Figure 1A shows a typical headphone circuit, and Fig. 1B shows its essential technical features. Resistor Ro in series with each headphone channel is chosen to provide an appropriately small amount of power to the headphone. It can even be thought of as providing an intentional mismatch between amplifier and headphone.
The impedance of the source feeding the headphone is essentially equal to Ro, typically much greater than the impedance of the headphone load, Z. Now consider our objective of delivering comparable amounts of power into two significantly different impedances. We will call the lower of these ZL (perhaps 8 ohms) and the higher one ZF, (let us say 600 ohms). Imagine that the internal, or source, impedance (Rs) of the new headphone driving circuit were a value between ZL and ZH . When the load is ZL, there is a mismatch between the source and the load due to the fact that Rs is higher than ZL. When the load is ZH, there is a mismatch due to the fact that Rs is lower than ZH. By properly choosing the value of R s, these two mismatches may be made equal in magnitude, and thus the same power will be delivered to each headset.
This value of Rs is √ZLZH, and is given in Table 1 for the most common combinations of ZL and ZH. However, in most cases we cannot simply replace the R o resistors in the present headphone circuit with resistors of value R_s. This is because Rs is usually significantly smaller than the source impedance, R_O. Hence the resulting power to either headset would be much greater than with the original circuit, requiring the amplifier to be operated at an unnaturally low volume level when headphones were in use.
In Fig. 2 we see a hypothetical circuit which solves this problem. The source impedance has indeed been made R s, but step-down transformer T1 has been added to reduce the voltage supplied to the circuit to a value producing the same power into the headsets that would have been delivered by the original (R o) circuit into the headset impedance for which it was intended.
Fortunately, in most cases the transformer can be eliminated by the circuit of Fig. 3A. So far as the behavior of this circuit at the output terminals is concerned, it can be considered identical to the circuit of Fig. 3B. The equivalent source voltage of this second circuit, E_E, is the true driving voltage, E1, reduced by the voltage dividing action of R1 and R2. The equivalent source impedance, RE, is the value which would be obtained by connecting R, and R, in parallel.
Thus, by properly choosing the values of R1 and R2, we can create a circuit which acts like the circuit of Fig. 2, the voltage-divider action exactly replacing the voltage step-down provided by the transformer, T1, and the equivalent source impedance (RE) having the value desired, Rs. If Rs were larger than R o transformer T1 would have been a step-up transformer, and no choice of R1 and R2 could be made which would allow the circuit of Fig. 3A to replace the circuit of Fig. 2. This situation rarely arises with conventional audio power amplifiers.
The equations for determining the values of R1 and R2 are given in the box.
Fortunately, for the impedance values, and values of R o encountered in most applications of this circuit, we can use a compromise circuit which avoids replacing the original series resistor, R o , with a new resistor, R , . We merely leave the present R o resistor(s) in the circuit and add, in parallel with each, a resistance which we shall call RP. By proper choice of RP, the source impedance becomes Zs, as originally desired, and equal power will be delivered to headsets of either impedance. Although this power level may be slightly different from that delivered by the original (unmodified) circuit, in most situations the difference will be far less than the differences in headset power level provided by different amplifiers, for example. And this circuit is easy to install, involving only addition of the two resistors RP in parallel with the headphone connections.
Table 2 gives appropriate value of RP for combinations of an 8 ohm headphone impedance and various higher impedances, as well as for various values of R_o originally present in the amplifier. For all combinations, the difference between the power level supplied by the new circuit and that supplied by the original circuit is less than 3 dB. The values in Table 2 have been rounded to the nearest Radio TV Manufacturers' Association value for 20% resistors. If the value of R o desired is not in the table, use the nearest listed value. The power dissipated in the Rp resistors is very small, and 1/4 watt carbon resistors may be used. If space permits and since they are more easily available, 1/2 watt or larger resistors may be used.
In most modern amplifiers, the most convenient location for the added resistors is right at the jack. The common (ground) end of each resistor can be connected to the common (sleeve) terminal of the jack, with the other end of the two resistors going to the tip and ring terminals. Figure 4 shows the final circuit.
For those interested in applying these circuits to situations not covered by the tables, the box gives the equations needed to calculate the various values.
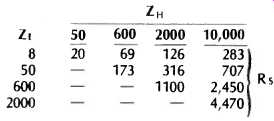
TABLE--1 R_s values for equal power into various values of Z_L and Z_H (ohms)

TABLE--2-Load impedance, 8 and: To determine values of R_P, which in parallel
with present resistor R_o will produce equal power into various load combinations.
(All values ohms)
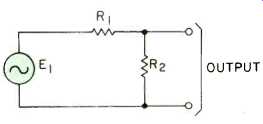
Fig. 3A--Voltage divider circuit.
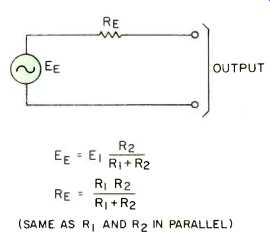
Fig. 3B--Equivalent voltage divider circuit.
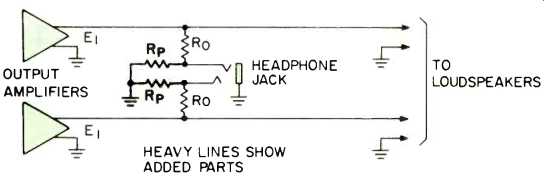
Fig. 4--Final dual-impedance headphone circuit.
It would often be desirable to provide dual-impedance headset operation for the monitor circuit of a tape recorder. However, if the present monitor circuit feeds directly from the line output of the recorder, or from a low-power headphone amplifier, then the circuit described by this article probably cannot be used. This is because such lower-power sources usually have low values Ro, and as previously mentioned the dual impedance circuit cannot handle the case where R s is to be greater than R_o. Another way to characterize this limitation is that a low-power source cannot deliver adequate power to a headphone through the impedance mismatch upon which operation of the "dual impedance" circuit depends. If the headphone monitor circuit is driven from an internal loudspeaker amplifier, with series resistors, as in Fig. 1, then this dual-impedance circuit can be applied.
Equations
To determine impedance, R_s needed to provide equal power into loads Z1 and Z_H (Ref. Fig. 2):
(1) R_s = √ (ZL - ZH).
Series resistance, R1, and shunt resistance, R2, to give source impedance Rs and to deliver the same power to loads ZL or ZH as the original circuit (Fig. 1) would have delivered to load of impedance Z1: (Ref. Fig. 3A)
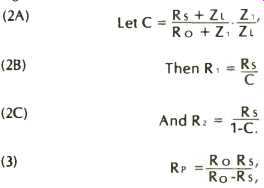
Shunt resistance, RP, to produce the desired source impedance Rs while keeping the series resistance at its initial value, R o (Ref. Fig. 4). The use of this approach produces equal power in loads ZL and ZH, but this power level is most generally different from that which would have been delivered by the original circuit to a load of Z. The shift in level from that of the original circuit is given by the equation:
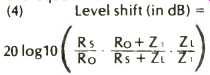
Negative values (i.e., quantity in parentheses less than 1) represent less
power delivered by the new circuit than by the original. For ease in interpretation,
the following table gives the values of the quantity in parentheses for various
level shifts:

(adapted from Audio magazine, May 1975)
Also see:
Piezoelectric Headphones (May 1975)
= = = =