
By W. J. J. Hoge
[Acoustical Engineering Manager, CTS Corporation, Elkhart, IN 46514, USA]
The first description of what is normally called a transmission line loudspeaker was published in 1936 by Benjamin Olney (1). The system was the "acoustical labyrinth" which he patented in 1934 (2) and represented an attempt to overcome the poor performance of the open-back cabinets of console radio sets. Olney's employer, Stromberg Carlson, produced the system for a few years during the '50s until they left the component high fidelity market. Transmission line systems did not really begin to catch on until after 1965.
In that year A. R. Bailey published a transmission line system construction article (3). Since then, several manufacturers have placed such systems on the market.
In the past few years the performance of direct-radiator loudspeakers has been well analyzed and methods for synthesizing optimum design specifications have been developed (4, 5, 6). These techniques have been successful in many applications (7, 8), however, until very recently, the theory of transmission line loudspeakers has not been very well understood (9). Direct-radiator loudspeakers are divided into three types, closed-box, vented-box, and passive radiator systems. Similarly, there are three types of transmission line systems. For the sake of brevity, let us call them Type A, Type B, and Type C. In Type A systems, the back side of the driver radiates into a sealed enclosure, while the front is coupled to a transmission line. The system output is solely from the output end of the line.
Type B and C systems allow the front side of the driver to radiate into the listening area, while the rear of the driver is connected to the transmission line, usually via a coupling volume. For Type B systems, the far end of the line from the driver is blocked. Type C systems have an aperture at the far end of the line so that the signal in the room is the sum of the outputs of the driver and the transmission line. What goes on in these systems, and is one better than the other? To answer these questions, we must analyze the systems.
Using Signal Flow Graphs
There are several common techniques for system analysis. The most popular is the dynamic analogy method which allows an equivalent electrical circuit of the loudspeaker to be drawn. However, another method, state-variable analysis, is this author's favorite. This method uses signal flow graphs instead of equivalent circuits (10).
That's nice. What's a signal flow graph?
Well, a signal flow graph is a way of writing a set of equations for a system and then interconnecting them so that the system can be analyzed. Consider the system in Fig. 2. (Kindly Editor's Note: This is the newly designed symbol for the U.S. Patent Office.) A voltage is applied to the lamp by the battery, and a resulting current flows. If the battery potential is E volts and the resistance in the current is R ohms, then the current I is given by Ohm's Law:
(Eq. 1)
A signal flow graph of the equation would look like this:
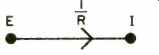
(Sfg. 1)
The dot is called a node. The line with the arrow……is called a branch. A node represents some physical quantity in which we are interested, while a branch shows the relationship between the two nodes which it connects.
Now, let us develop a simplified signal flow graph of a transmission line loudspeaker.
We start with the electrical input from the generator Eg. It causes a current in the voice coil Ivc. If RE is the voice coil resistance, then we have
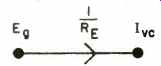
(Sfg. 2)
The current in the voice coil interacts with the magnetic field to produce a driving force on the diaphragm Fp. If B is the flux in the gap and I is the length of the wire in the gap, then
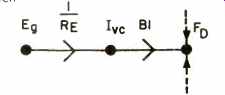
(Sfg. 3)
Note that some additional branches are entered in the Fp node. This is because other parts of the system are "pushing" on the diaphragm and contribute to the total force.
We'll crank them in a bit later.
Newton's Second Law of Motion tells us that if we push on something, it will accelerate. The acceleration of the diaphragm ap with effective mass MMS is given by:
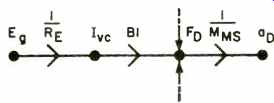
(Sfg. 4)
The velocity of the diaphragm up is found by the equation:
uD = integral aD dt (Eq. 2)
At this point we hear screams of despair from those Gentle Readers who did not take calculus (and some who did and know that integral calculus is a pain in the neck, or perhaps someplace lower). But have no fear! The author has a trick up his sleeve. Under certain conditions (This Engineering technique is known as "arm-waving" and is usually accompanied with the magic words, "It can be shown that..."), of which this is one, we can turn calculus into simple algebra by saying that
s = d/dt (Eq. 3)
If this is true, then
1/s = integral dt (Eq. 4)
Thus it can be shown that
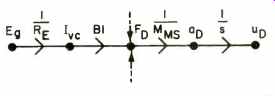
(Sfg. 5)
In a similar manner we integrate up to find the displacement of the diaphragm xp.
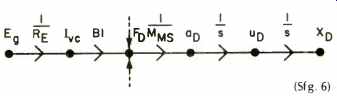
(Sfg. 6)
We can complete the signal flow graph for the driver by adding a branch from xp to FD to give the restoring force from the compliance of the suspension CMS, a branch from up to Fp to give the force opposing motion of the diaphragm caused by mechanical losses RMS, and a branch from up back to the voice coil circuit to represent the voltage generated when the coil of wire moves in the magnetic field.
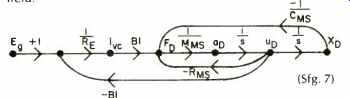
(Sfg. 7)
The minus signs indicate that the restoring force and the losses oppose the driving force and that the voltage generated by coil motion opposes the input signal.
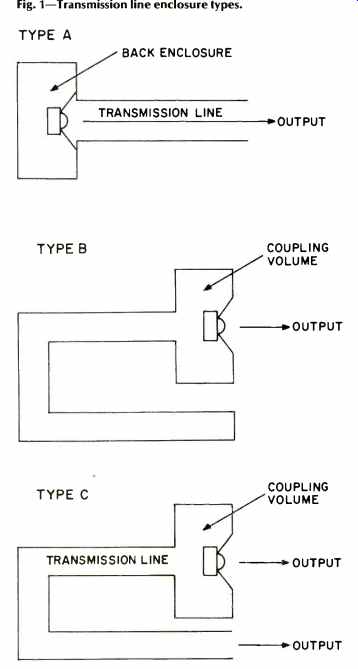
Fig. 1--Transmission line enclosure types.
The mechanical motion of the diaphragm causes a current of air (or volume velocity) Up to flow into the room. Also, a volume velocity UB flows into the enclosure. Obviously, UD is 180° out of phase with UB, but the two are of equal magnitude. UB causes a pressure variation pB in the enclosure given by
PB = 1/CAB integral UB dt (Eq. 5)
where CAB is acoustic compliance of the air in the en closure (or coupling chamber). If SD is the area of the diaphragm, then
(Sfg. 8)
...which is the signal flow graph of a closed-box loudspeaker.
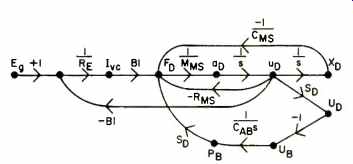
To get a Type A system, we need only add the throat impedance zAT of the transmission line to the system. We can then find the throat pressure pT and the system output power, PA. Fig. 3 gives the signal flow graph of a Type A system.
For the type B and C systems zAT is connected to the back of the diaphragm. See Figs. 4 and 5.
Analyzing System Types
Now that we've got an analytical picture of the system, we should be able to figure out how it works. Type B is the simplest case. Note that we have used an italic z rather than a plain Z for zAT. This is to signify that zAT varies with frequency. What effect does this have on performance? Consider the case of a constant diameter tube for the line. The behavior of the driver is easily determined at various frequencies. Acoustic waves from the driver travel down the line and reached the blocked end. The sealed end is an infinite acoustic impedance (a situation analogous to an open circuited electrical line) (24). This termination of the line yields a reflection coefficient of -1. At some frequency, the line length is equal to a quarter-wavelength of the acoustic signal. The reflected wave travels back down the line and strikes the driver diaphragm in such a way as to assist its motion. This produces a peak in the output. At twice that frequency, the line is a half-wave length long. In this case, the reflected wave opposes diaphragm motion and system output drops. Whenever the line length is equal to an odd number of quarter-wavelengths, there is an increase in diaphragm output. When the line is some multiple of a half wavelength, the diaphragm output drops. Since the diaphragm is the only source of output, the response has many peaks and dips. This is certainly unsuitable for high fidelity reproduction.
The response may be smoothed by filling the line with some sort of damping material (e.g., fiberglass or long-fiber wool). This turns zAT into a resistor. It also makes the system perform like a leaky closed-box system, and low efficiency results. A simple, well-designed closed-box system would clobber a Type B system of equal cabinet volume. So, Type B systems are not the optimum approach.
Type C systems, however, have some possibilities. As in a vented-box direct-radiator system, we have an additional source of output (the line mouth) to assist the driver. Once again, the line throat impedance zAT varies with frequency.
The line is terminated with an open aperture which has a relatively low acoustic impedance (analogous to a shorted electrical line). The behavior is opposite of the Type B; the reflection coefficient is essentially +1. When the line is an odd number of quarter-wavelengths long, the line presents a high acoustic impedance to the driver and most of the driver's output is delivered to the line.
When the line is an odd multiple of a half-wavelength long, the reflected wave will assist the driver and the driver distortion are the only considerations, a horn-loaded Type A system is optimum. If size and price are part of the picture, then a vented-box direct-radiator (at least for the woofer) may make some sense.
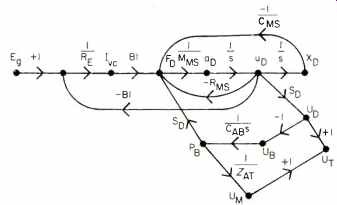
Fig. 5-Signal flow graph of a Type C transmission line
loudspeaker.
Fig. 6-Optimized Type A transmission line loudspeaker.
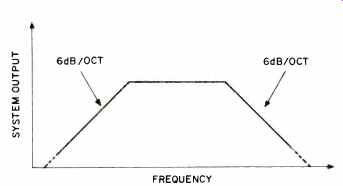
Fig. 7-Frequency response of the simplified model.
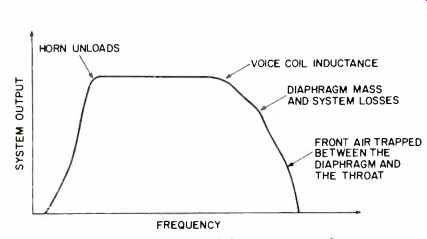
Fig. 8-Frequency response of the more complete model.
Acknowledgements
The analysis of the Type B and C transmission line systems was based on a method developed by G. S. Letts. The horn analysis was based on a model originally developed by D. B. Keele, Jr., whose comments, along with those of R. H. Small, J. R. Ashley, and W. M. Leach, were most helpful.
References
(1) B. Olney, "A method of eliminating cavity resonance, extending low frequency response and increasing acoustic damping in cabinet type loudspeakers," Jour. Acoust. Soc. Amer., Oct, 1936.
(2) B. Olney, U. S. Patent 2,031,500. (3) A. R. Bailey, "A non-resonant loudspeaker enclosure design," Wireless World, Oct. 1965.
(4) A. N. Thiele, "Loudspeakers in Vented Boxes," Proc. IRE ( Australia), Aug. 1961.
(5) R. H. Small, Direct-Radiator Electrodynamic Loudspeaker Systems, Ph. D. Thesis, Univ. of Sydney, 1972.
(6) J. E. Benson, "Theory and Design of Loudspeaker Enclosures, Part 3-Introduction to Synthesis of Vented Systems," A WA Tech. Rev., Nov. 1972.
(7) R. J. Newmann, "A Loudspeaker System Design Using a Sixth-Order Butterworth Characteristic," Jour. Audio Eng. Soc., July/Aug, 1973.
(8) W. J. J. Hoge, "Switched-On Bass," Audio, Aug. 1976.
(9) G. S. Letts, A Study of Transmission Line Loudspeaker Systems, Honours Thesis, Univ. of Sydney, 1975.
(10) J. R. Ashley, et. al., "Signal flow graphs for electro acoustic transducers (or modeling made easy)," Simulation, Nov. 1976.
(11) W. J. J. Hoge, "State-Variable Analysis of Horn Loudspeakers," presented at the 57th Convention of the Audio Eng. Soc., Los Angeles, 1977.
(12) D. B. Keele, Jr., "Low-Frequency Horn Design Using Thiele/Small Driver Parameters," presented at the 57th Convention of the Audio Eng. Soc., Los Angeles, 1977.
(13) R. H. Small, "Suitability of Low-Frequency Drivers for Horn-Loaded Loudspeaker Systems," presented at the 57th Convention of the Audio Eng. Soc., Los Angeles, 1977.
(14) D. B. Keele, Jr., "Optimum Horn Mouth Size," Audio Eng. Soc. Preprint No. 933.
(15) D. B. Keele, Jr., "What's So Sacred About Exponential Horns?," Audio Eng. Soc. Preprint No. 1038.
(16) A. G. Webster, "Acoustic Impedance and the Theory of Horns and the Phonograph," Jour. Nat. Acad. Sci., May 1919.
(17) C. R. Hanna and J. Slepian, "The Function and Design of Horns for Loudspeakers," Trans. AIEE, Feb. 1924.
(18) W. M. Hall, "Comments on the Theory of Horns," Jour. Accoust. Soc. Amer., Apr. 1932.
(19) P. W. Klipsch, "A Note on Acoustic Horns," Proc. IRE, July 1945.
(20) P. W. Klipsch, "A High Quality Loudspeaker of Small Dimensions," Jour. Accoust. Soc. Amer., Jan. 1946.
(21) H. F. Olson, Elements of Acoustical Engineering, D. Van Nostrand Company, New York, 1940. (22) L. L. Beranek, Acoustics, McGraw-Hill, New York, 1954.
(23) D. B. Keele, Jr., "An Efficiency Constant Comparison Between Low-Frequency Horns and Direct-Radiators," Aud. Eng. Soc. Preprint No. 1127.
(24) J. L. Potter and S. Finch, Theory of Networks and Lines, Prentice-Hall, Englewood Cliffs, New Jersey, 1963.
(Source: Audio magazine, Aug. 1977 )
Also see: TIME ALIGNMENT in loudspeakers (Aug. 1977)
= = = =