
by R. A. Greiner
[R. A. Greiner is Professor of Electrical and Computer Engineering at the University of Wisconsin, Madison. He teaches and does research in electroacoustics, acoustic measurements, applications of digital signal processing, audio system design, and noise control. He holds over a dozen patents in electronic instrumentation and audio systems and was elected a Fellow of the Audio Engineering Society in 1984.]
This article is adapted from a paper which I wrote and presented to the Audio Engineering Society 10 years ago, and which was later published in the Journal of the Audio Engineering Society (Vol 28, No. 5. May 1980), original paper discussed the issue of cables used for connecting pouter amplifiers to loudspeakers. In the intervening years, an entire industry for the manufacture of special cables has grown up around this issue. I have therefore added comments to expand the notions presented in the original paper and to bring it more up to date. The paper has also been edited slightly to make it clearer to persons not entirely familiar with some of the electrical engineering terms used. The substance of the paper, however, is based on electromagnetic theory, and no amount of advertising in the past 10 years has changed that base.
Loudspeakers seem to be connected to power amplifiers with greatly varying degrees of care. The professional generally selects wiring of appropriate size and type for the given application, while many others are quite casual about such matters. Recently, however, considerable attention has been drawn to the issue of loudspeaker cables by the appearance of numerous "special" cables with properties that allegedly improve the quality of the sound delivered by the loudspeaker.

While most of these claims are no more than pure fantasy, there is just enough edge of truth showing to make a hard look at loudspeaker cables seem appropriate.
In this article, loudspeaker cables are investigated to determine whether or not their transmission-line behavior is significant for audio frequencies.
Conclusions are reached regarding the validity of lumped equivalent representations of short transmission lines.
Certain critical frequencies are calculated and measured to estimate the effect that the cable will have on the amplifier and the loudspeaker load.
The problems caused by the resistance of the crossover, level pads, and any fuses in the circuit are considered briefly.
Cable Parameters
The parameters which describe the cable electrically are series resistance, series inductance, shunt conductance, and shunt capacitance. These parameters can be determined by direct measurement and/or by calculation from elementary formulas. They depend entirely on the geometry of the cable and the nature of the conductors and the insulation used. The approximate values for a variety of cables made of copper wire and rubber or plastic insulation are summarized in Table I. Conductors of copper, silver, or similar high-conductivity materials-regardless of the method of drawing the wire-behave similarly. The electrical properties of cables are not significantly affected, at audio frequencies, by the type of insulation used. The mechanical properties of the cable, however, may be more desirable with use of certain insulators and construction techniques.
Note that the larger the physical size of the wire, the smaller its gauge number, and that each change of three wire-gauge sizes doubles or halves the wire's cross-sectional area. The nature of the insulation, and whether or not the wire is "tinned," have little effect on the electrical parameters of the cable at audio frequencies.
The accompanying Tables, based on my 1979 investigations, cover both "normal" and selected "special" cables. Three of the normal cables are typical two-wire pairs, such as standard zip cord with rubber insulation. Of these, the No. 12 zip cord is a European extension cable made by Lucas; its wires are more widely spaced than those of U.S. extension cords, giving it a slightly higher inductance. Two of the other normal cables are standard twisted-pair types in a vinyl jacket, normally used by professionals; these are available from Alpha, Belden, Consolidated, and other manufacturers. The RG9 is a standard coaxial cable made, in this instance, by Belden.
Of the three types of special cables included, one is a large-gauge coaxial of dual-cylindrical construction by Mogami. Another is a braided cable by Cobra. The third is a plastic-jacketed pair of "welding size" conductors--real welding cables, I believe-from Fulton.
Present-day cables that deviate from the techniques used to construct cables in 1979 usually use fine strands of wire which are gathered or braided in a variety of complex geometries. Some of these techniques increase and some decrease the series inductance of the cable slightly. Both techniques, increasing and decreasing inductance, are claimed to improve the electrical properties of the cables. In the following discussion, it should be apparent that neither of these techniques makes much difference at audio frequencies.
A review of Table I is interesting since it shows that something quite drastic has to be done to the geometry of the cable before its inductance or capacitance per unit length changes very much. The normal cables, even including the welding-cable pair, have values of inductance and capacitance within a factor of about 2. The resistance of the thicker wires, of course, goes down greatly. Skin-depth phenomena have only a slight effect on copper wires at audio frequencies. The skin depth for copper at 20 kHz is about 0.5 mm. Thus, wires larger than No. 14 gauge will have a resistance, at 20 kHz, slightly higher than the d.c. value. The ratio of the 20 kHz to d.c. resistance is given in Table I.
The wire listed as No. 12 zip cord is a high-quality extension-cord style of construction with slightly greater than normal spacing. Thus, it has a slightly higher series inductance compared to domestic zip cord. This cable and the welding type fall just slightly outside the range of values for normal wires (one above and one below). The issue of Litz-type wire construction, using a multitude of tiny strands, could be discussed at length, but at this point, let it be said that the topic is largely irrelevant at audio frequencies.
There simply is no significance to "skin effect" at audio frequencies, and wires which purport to fix this effect usually do not do so in any case.
Spacing the wire pair more closely has the advantage of reducing the series inductance. Unfortunately, this tactic also increases the shunt capacitance substantially. Various braided cables seem to attain a reduction of three or four times in the series inductance, but show a rise of 10 to 20 times in the capacitance. Whether the advantages of this type of construction outweigh the disadvantages will be considered later. Some users have suggested spacing wires farther apart to give less "interaction" between the wires. However, it is well known that the inductance of a cable rises as the wires are spaced farther apart. This effect is shown in Table II. Spaced wires not only interact more with each other but also show crosstalk with other nearby pairs. Spacing the wires offers no advantages whatever and several serious disadvantages. This configuration should never be used and will not be considered further here.
Some regular coaxial cables have attractive values of inductance and capacitance. However, only a few of the larger sizes have large enough conductors to make them useful for loudspeaker connections. Standard RG-9 has been included in Table I. One sample of a special coaxial cable consisting of two concentric cylinders of stranded wire has been included as well. This coaxial cable is of No. 12 gauge and is specifically designed for low-impedance transmission-line purposes.
Cables as Transmission Lines
When considering cables as transmission lines, thoughts come to mind of characteristic impedance, termination, matching, reflections, and frequency dispersion. All of these are valid concepts, but they are not usually considered for very short transmission lines. And indeed, any reasonable--length loudspeaker cable is a very short line. The wavelength of a 20-kHz signal is about 10 miles (16 km). Thus, a 10-meter cable is 1/1,500 of a wavelength. Any fluctuations in the signal caused by reflections at the ends of this cable will take place at a frequency of 30 MHz. Or, to look at it another way, 1,500 iterations toward the final voltage distribution in the cable will take place every cycle at 20 kHz. One must conclude that there are absolutely no audio frequency effects related to these reflections for cables of any reasonable length.
It is fortunate that reflections in loudspeaker cables are irrelevant, since they are never matched at either the amplifier or the loudspeaker ends. In practice, both the source and the load are quite complex and frequency dependent. Nevertheless, it is interesting to take a look at the characteristic impedance of a typical loudspeaker cable, which is also quite complex.
The characteristic impedance of ,a transmission line is given by:
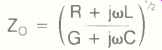
R is the line resistance per unit length, L is the series inductance per unit length, C is the shunt capacitance per unit length, and G is the shunt conductance per unit length. Of the two constants, j is the square root of -1 and w is equal to two times the frequency.
For all practical loudspeaker cables, G equals 0. Thus, for high frequencies, where wL >> R, we have:
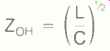
This is an impedance called the characteristic impedance. It is given for selected cables in Table I. For low frequencies, where
wL << R, we have:
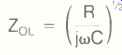
This expression is the correct one for frequencies which fall below a value fm, which can be defined as R divided by 27 π L, and which is typically somewhere in the middle to upper audio band. For the physically smaller normal cables, fm is about 13 kHz; it is about 520 Hz for physically larger welding cable, 40 kHz for braided cable, 30 kHz for cylindrical coaxial cable, and about 26 kHz for regular coaxial cable.
For frequencies well above fm, the cable behaves more ideally in the sense that there is no frequency dispersion in the line, and the impedance has reached a limiting value that is resistive. At lower frequencies, the impedance is complex, and the line contributes some frequency dispersion to the signal. When there is dispersion in the line, the high frequencies arrive at the end of the line ahead of the low frequencies. This happens because the line's series inductive reactance is too small compared to its resistance.
The principles of transmission-line theory require that for purely distortionless transmission:
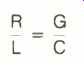
Since G equals 0 for typical audio cables, it is impossible to make the line perfect. However, R should be made small and C should be made small as well. When this has been done to the greatest extent possible, then L should be made larger. The telephone company does just this by inserting loading coils in long lines to reduce dispersion distortion.
It would appear that reducing series inductance, as some special cables do, does not make much sense from a transmission-line viewpoint. When cables are considered as lumped element circuits, however, there are some good reasons to decrease all of the elements as much as possible; this will be discussed below. First, it is interesting to calculate the dispersion for some typical loudspeaker cables.
Since all loudspeaker cables show some amount of loss and some dispersion, a vital question to be answered is: How much? To determine the difference in the arrival times of the high frequencies compared to the low frequencies, we need to find the group velocity of the transmitted signal. This is given by:
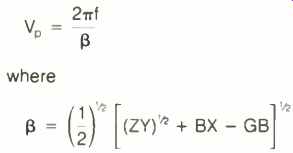
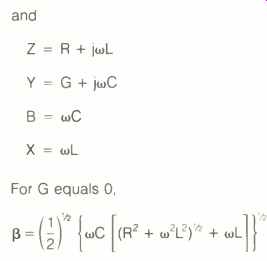
Dispersion characteristics for selected cables are shown in Table III for frequencies of 100 Hz and 10 kHz. From the Table, it is apparent that for a 10 meter cable, the delay differences are only a fraction of a microsecond--except for the braided construction which is a little worse. In any case, the delay time, or frequency dispersion, certainly not a problem for loudspeaker cables of any reasonable length.
Before going on to the lumped parameter treatment of short lines, w should make one additional general observation about transmission lines A line will look much like a shunt capacitance when it is loaded with a impedance much higher than its characteristic impedance, and it will look like a series inductance when loaded by an impedance much lower than its characteristic impedance. Almost a loudspeaker cables are loaded ac cording to the latter criterion. In general, playing numbers games with the high-frequency value of characteristic impedance for short cables at audio frequencies is largely useless.
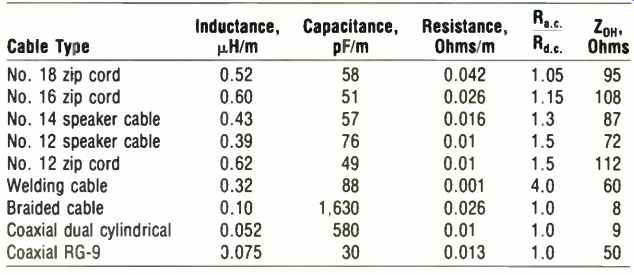
Table I--Typical loudspeaker cable parameters. The ratio in the fifth column
is impedance divided by d.c. resistance.
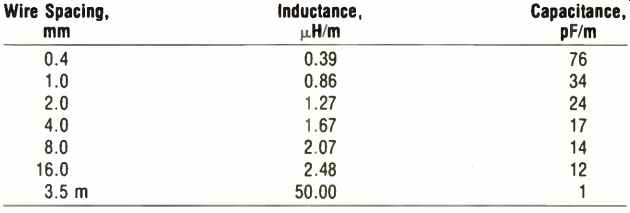
Table II--Parameters of spaced wires for No.12 gauge wire.
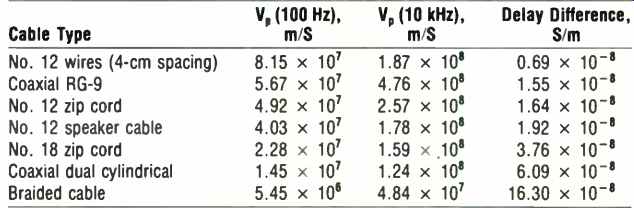
Table III--Dispersion characteristics of selected loudspeaker cables, in
order of dispersion, showing propagation velocity at two frequencies and
the delay difference between them.
Cables as Lumped Lines
It should be clear that treating loudspeaker cables as transmission lines, while interesting, is not of much direct design value. The loads are complex, the lines very short, and the frequencies too low to allow easy, ideal treatment. Exact treatment is more complex than is warranted. In this section, loud speaker cables will be treated as wire pairs that can be represented as lumped element equivalent circuits. This method will give reasonable design guidance and intuitively sensible results. A satisfactory equivalent circuit for an amplifier/cable/loudspeaker circuit is shown in Fig. 1. In order to have convenient numbers to use for examples, the values for typical cables 10 meters in length are given in Table IV. Applications using shorter or longer cables can be scaled up or down from these examples.
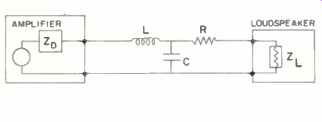
Fig. 1--Amplifier cable loudspeaker circuit using lumped circuit elements
to represent the properties of the cable, typical R. L. and C values for
cables 10 meters long are given in Table 4.
There are at least two major interactions to consider in the system shown in Fig. 1. One is the interaction of the amplifier with the total load, including the cable; the other is the interaction of the loudspeaker with the amplifier, including the cable. Since the system is so tightly coupled, some consideration to the nature of Zo and ZL must be given. While it is not possible to consider all possible cases, certain more common ones will be discussed. First consider the amplifier end of the high-fidelity system.
An ideal amplifier would be a voltage source with a Zo of zero. In fact, many high-quality amplifiers come very close o this ideal. At low and middle frequencies, the output resistance of an amplifier will typically be less than 0.05 ohm, with a rise to 0.2 ohm at the very highest frequencies. The output will usually be slightly inductive. Often a series inductance of 2µH will be used o isolate the amplifier feedback loop from capacitive loads. This inductance s 0.25 ohm reactive at 20 kHz. A good amplifier should be stable for any load, including capacitive loads.
Since even the worst of the cables is only 0.2 µF for 10 meters, such a cable should not cause a good amplifier to become unstable or to ring. It would take 35 µF to resonate 2µH at 20 kHz.
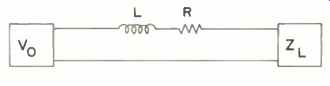
Fig. 2--Simplified circuit for a “good" amplifier driving a cable and
loudspeaker load. Critical frequencies for this' circuit are summarized by
Table V.
Thus, amplifier/cable interaction problems in the audio band are not likely.
However, it is known that some amplifiers will not tolerate even slightly capacitive loads. This is an amplifier design problem, not a cable problem, and should be dealt with at that level. It s easy to test amplifiers for load sensitivity problems, and those amps that are not satisfactory should be eliminated. We will assume that the amplifier/ cable interface question is settled by using a "good" amplifier. The problem of fuse-protecting the output circuit is not trivial and will be discussed later.
With a good amplifier in place, the remaining electrical problems are related to how the loudspeaker loads the cable and interacts with it. It is possible to simplify the equivalent circuit a bit with the assumption that the amplifier can, at the very least, drive the cable capacitance. An appropriate' circuit is shown in Fig. 2. While the values of the series resistance and inductance for the cable are easily measured, well known, and well behaved, such is not true of the load. The simplest equivalent circuit for a loud speaker will be a series resistor/inductor combination. But real loudspeakers consist of crossover networks with inductors, capacitors, resistors, trans formers, and voice-coils, all in some complex combination. Fortunately, it is not necessary to consider all possible combinations but only some limiting, worst cases. At low frequencies, most loudspeakers become mainly resistive, and some have a rather low value of resistance. Often the lowest value is below the rated impedance. Let us assume that this value never gets lower than one-half the rated impedance. If the loudspeaker becomes inductive at higher frequencies, as most cone-type drivers do, there should be no problems worse than the low-frequency problems. It is possible, however, with capacitive tweeters, ribbons, or some more unusual tweeters to have low-impedance effects in the loudspeaker at the high frequencies. It will therefore be wise to investigate resistive, capacitive, and inductive loads at about one-half the rated impedance at the high-frequency end of the spectrum as well.
The low-frequency end of the spectrum will be taken as 20 Hz and the high-frequency end as 20 kHz.
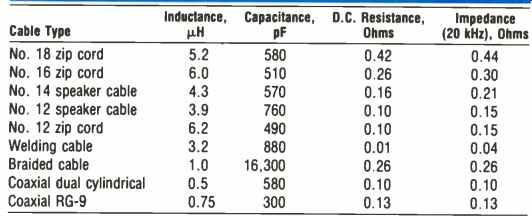
Table IV--Lumped element values for 10-meter lengths of cable.
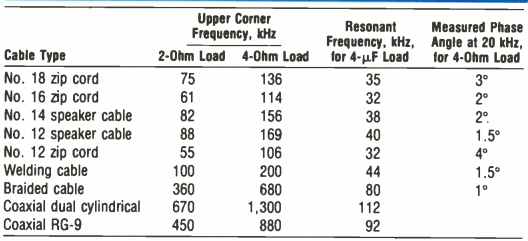
Table V--Frequency limitations for 10-meter lengths of cable with various
loads.

Table VI--Worst-case distortion for power bursts just short of those necessary
to burn out the fuse at any frequency.
Using the simplified equivalent circuit of Fig. 2, several frequencies of interest have been calculated. The first is the upper corner frequency for a load that is low and resistive at very high frequencies. While this is not a likely load, it is a worst possible case. It is the case for which the cable series inductance causes a roll-off of the high frequencies. For any realistic load, with some inductance, the cable inductance will be entirely swamped out by the load, of course. A second is the frequency at which the cable inductance and a highly capacitive load will resonate. The capacitive load is chosen as 4µF, which would correspond to a 2-ohm impedance at 20 kHz.
While such a load is quite unreasonable, it represents a possible worst case. The frequencies given in Table V thus represent the lowest possible values for about the worst possible loading one could consider driving. All of the frequencies are well above the audio spectrum. However, they are not so high that if the cable lengths were doubled, they would be of no interest at all.
It appears that, as common sense would tell us, one should not try to drive a loudspeaker of very low impedance at great distances, or that one should use higher impedance loudspeakers if long cables are necessary.
With most normal listening room situations, the cables will be short enough so that no audio frequency problems arise from the loudspeaker cables. It is interesting to note that changing to larger wire has little effect on the high-frequency resonance or fall-off frequencies. Those frequencies are controlled by the series inductance. Thus, there is some rationale for using cables that have low series inductance. Standard coaxial construction of the cable seems to give all of the advantages of low series inductance without the serious disadvantages of high shunt capacitance.
Since most loudspeakers have their lowest impedance at low frequencies, there are some advantages in using physically larger wire, with its lower series resistance. One advantage is reducing losses of power in the connecting wire; another is preserving the high damping factor of the power amplifier. It seems unlikely that for runs of under 30 meters and with normal loudspeakers, there is any reason to use wire larger than No. 12 gauge for even the highest fidelity applications.
A large number of cables with resistive, capacitive, and real loudspeaker loads were measured using sensitive, broad-band, difference amplifier techniques. Resistive loads were more difficult to drive than typical loudspeakers.
Capacitive loads were slightly more difficult still. Electrical problems of any kind (that is, phase shift, attenuation, dispersion, etc.) with 10-meter cables driving normal loudspeakers were just barely measurable using these refined measurement techniques. Absolutely no audible problems could be heard.
The best solution to cable problems by far is to move the amplifier to the loudspeaker, thus making the cable very short.
Loudspeaker Considerations
When discussing wires used to connect amplifiers to loudspeakers, it would be wise to consider the residual effect of the wiring within the loudspeaker itself. At low frequencies, the worst offender is the series resistance of the low-pass crossover filter-in addition to the voice-coil resistance, of course. After all, 20 meters of No. 18 wire in an inductor introduces just as much resistance as 10 meters of No. 18 connecting cable from the amp to the speaker and back again. With essentially all loudspeakers that have internal crossovers and/or level-control pads, the internal resistance and inductance totally swamp out any possible small effects due to the connecting cable. These internal resistances of the crossovers and pads in a typical loudspeaker generally obviate the usefulness of the high damping factor of a typical amplifier. The only way to get the amplifier signal directly to the voice-coil is to use crossovers ahead of the amplifiers and multiple amplifiers. In very high-quality systems, elimination of the internal passive crossovers is a step that might be taken to obtain improvement of the sound.
Therefore, very good advice for improving a system and essentially eliminating cable concerns is to place the amplifiers at the loudspeaker and eliminate the crossovers by multi-amplifying the system with electronic crossovers. The problem of getting the low-level signal to the amplifier from the source is relatively simple, since the impedance levels are relatively high and excellent coaxial cables have been available for many decades. This tactic also moves the power-level signals, hum, heat, and the like away from the signal sources and preamplifiers.
Many of these practices are normal, good engineering methods and are commonly found in professional audio systems.
Fusing the Output Circuit
All of the above problems have been concerned with linear circuit elements.
Ideally, the fuses used in the output circuit would be linear resistors as well.
However, since they have to get hot, and melt, to burn out, they are actually nonlinear elements in the output circuit. If fuses are to be useful, they must blow out when the system is used at some specified power level over the maximum desired. Typically, a fuse will increase in resistance to about three or four times its cold value just short of burnout. At 60% of full load, it will increase to about twice its cold value. A typical fuse blow-out cycle is shown in Fig. 3; the resistance change per cycle is clearly evident. The calculations and measurements of this section show some possible problems with distortion caused by these changes in the fuse during normal program reproduction.
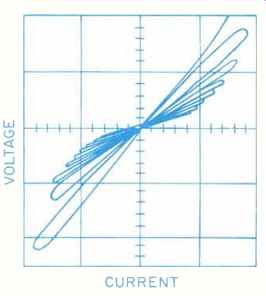
Fig. 3--Fuse-burnout cycle for a 20-hz signal large enough to cause burnout
in about 0.8 S. In this reproduction of an oscilloscope trace, the substantial
change in the slope of the voltage-current curve indicates a large resistance
change as the fuse element heats up.
Using the simple circuit of Fig. 4, it can be shown that for a typical, regular-speed fuse of the tubular type, the distortion produced could reach the values in Table VI. These figures represent intermodulation distortion for any frequency when the output circuit is pulsed with power bursts just short of fuse burnout. Typical measured modulation of a high-frequency signal when pulsed with tone bursts that are set at 60% of burnout are shown in Fig. 5.
This Figure shows the oscilloscope trace of a 5-kHz signal modulated by 20-Hz tone bursts. The tone bursts have been filtered out to show only the 5-kHz modulated signal. The heating and cooling cycle of the fuse is clearly visible. The time constants of typical fuses are such that this heat and, consequently, resistance cycling can take place for normal musical beats at low frequencies. To minimize interaction of this type across the frequency spectrum, it would seem wise to provide separate fuses for each frequency range of a multi-way system. Fast-blow fuses are worse than regular fuses since they change temperature 10 times more quickly. There is no solution to this problem except over-fusing or not using fuses at all, unless the fuses are included within the feedback loop. This can be done, of course, by putting the fuses in the power-supply bus or even within the normal feedback loop.
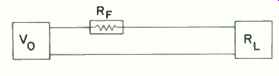
Fig. 4--Circuit for the series fuse often used for speaker protection. Possible
worst-case distortion figures for this circuit are given in Table 6.
Fig. 5--Cycling of fuse resistance with a 5-khz signal and a 20-hz tone
burst. In this reproduction of an oscilloscope trace, the burst is on for
eight cycles and off for 32 cycles, at 60% of the amplitude that mould cause
burnout.
Conclusion
It has been shown that loudspeaker cables need not be treated as transmission lines. It has also been shown that, in fact, transmission-line theory can give misleading results for very short lines, and that short lines should be treated as lumped lines. On the other hand, with poor choice of load and with longer cables, there may be some defects in phase or frequency response or some resonances introduced in the extreme upper audio frequency range.
It is clear that normal cables are suitable, and essentially perfect, compared to other defects in the transmission system--not the least of which is the loudspeaker crossover network and level-pad arrangement.
The use of special cables, including normal coaxial cable, is not warranted except in a few extraordinary applications. And in those particular applications short runs of cable would be a better solution.
Retrospect, 1989
There has been a great deal of interest in cables and interconnects in the years since this article was originally published. In fact, a whole industry has appeared. A number of new cable designs have appeared which have slight y different characteristics from the "standard" cables. Interestingly, these designs have gone in both directions at once, in that some increase inductance and some decrease it, some increase capacitance and some decrease it, some lower the impedance and some increase it, some reduce the time dispersion and some increase it, and so forth.
I have seen no scientific or statistically significant studies which show that all of the different designs have any significant or audible effect whatever on the transmission of audio frequencies in these cables. This is not to say, however, that there are not some common and sensible precautions which should be taken when wiring a system. I would recommend the following for consideration: Choose a cable that has reasonably low resistance-say, less than 5% of the lowest resistance of the loudspeaker at any frequency. Choose a twisted pair of wires to reduce or eliminate any possible crosstalk between wire pairs or from parallel power cords. Make connections on each end with proper spade lugs or screw terminals which can be firmly tightened. Additionally, it is a good idea with any cable--be it for loudspeakers or other interconnections--to look for a mechanically sound connector. Too many connectors are mechanically unreliable, with possibly one of the worst being the common RCA phono connector used on consumer equipment. Professional equipment uses XLR or BNC connectors, for good reason. Gold-plating is quite common today and certainly does no harm.
Recognize that while the sonic effects of cables have not been scientifically verified, it does no harm to use good-quality, more or less normal, cables. These are commonly available at modest cost, and their application gives psychological, and perhaps psycho-acoustical, satisfaction, which is of some value.
=============
(adapted from Audio magazine, Aug. 1989)
= = = =