By Dick Crawford
IT'S NOT FAIR. It's just not right. I mean the way more efficient loudspeakers are penalized in their bass response. They are, you know. Here, I'll show you why, and what you can do about it.
Using the nomenclature of Harry F. Olson', we can write the motional impedance of a loudspeaker as:
(1)
(Bl)^2 / Zmt
where Zem = motional impedance of loudspeaker in abohms,
B = flux density in air gap, in gausses,
l= length of the conductor in the voice coil, in centimeters, and
Zmt = total mechanical impedance of the mechanical system, in mechanical ohms.
Further, we can write the force exerted upon the loudspeaker cone as:
(2) f= Bli
where f= force, in dynes
i= current, in abamperes.
Now, suppose I had two loudspeakers, names “More” and “Less”. They are identical except that MORE has twice the flux density of LESS. Perhaps the greater flux density is due to a larger magnet. Both MORE and LESS are mounted in infinite baffles. Both speakers are driven at equal power levels by a good stereophonic amplifier. What do the above equations tell us? Obviously, the greater flux density of MORE gives it greater efficiency. How much greater? We can answer this with the aid of equation (2). The sound pressure generated by a loudspeaker is proportional to the force generated by its voice coil. Sound pressure is analogous to electrical voltage in that acoustical power is proportional to the square of sound pressure as electrical power is proportional to the square of the voltage across a resistor. If we double the force in (2), we quadruple the efficiency. Thus if we double the flux density in a loudspeaker while keeping the other factors (including the current flowing in the voice coil) constant, then we quadruple the efficiency.
Great! But do we keep the current constant if we change the flux density? Don't we alter the impedance characteristics when we alter the flux density? In most loudspeakers the impedance in the mid-range frequencies, where efficiency is specified, is dominated by the resistance of the voice coil windings. For woofers, sometimes the dominant impedance is the inductive reactance of the voice coil. This means that most of the electrical power delivered to a loudspeaker gets dissipated in the resistance of the voice coil rather than in acoustical power. This is why most loudspeakers are less than 10 per cent efficient.
Returning to our two loudspeakers MORE and LESS, we see that the resistance of both voice coils is identical, and thus the speaker impedances will be very similar over most of the frequency range. Thus the current in both speakers is nearly identical for equal drive levels. And this means that MORE is almost four times as efficient as LESS in the mid and high frequency ranges.
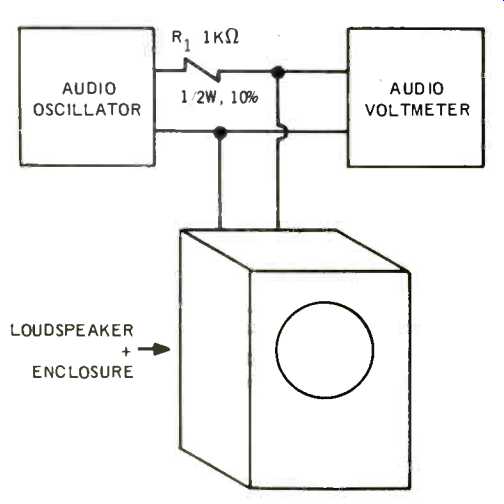
Fig. 1--Loudspeaker impedance test setup.
But what about the lower frequencies? At bass resonance, for example? Surprisingly, MORE is out of luck. Referring to (1), we see that the resonant impedance of a loudspeaker goes up as the square of the flux density. Thus MORE will have four times the electrical impedance at resonance of LESS. This means lower current, less force, less sound pressure, and lower efficiency for MORE at bass resonance. The sound pressure of MORE is one half that of LESS at resonance, and the efficiency is one quarter! Foul play! No wonder low efficiency speaker systems have done so well.
Well, then, why do we want efficiency? For one thing, a more efficient loudspeaker has better damping', and thus better transient response and a somewhat smoother frequency response. A high efficiency loudspeaker needs a lower power amplifier. Most component type high fidelity loudspeakers are of the high efficiency type.
So we have a loudspeaker. What can we do if it lacks bass? We can equalize. By equalize I mean bass boost in the amplifier. Bass boost? Does not proper equalization depend upon a complete knowledge of the loudspeaker parameters such as mass, compliance, flux density, et al? Or perhaps an acoustical laboratory with an anechoic chamber, expensive microphones, and so forth? No, I contend that an adequate job of equalization can be carried out just using an audio oscillator, a one k-ohm resistor, an audio voltmeter, and the speaker in its enclosure. Figure 1 shows the test set up.
The first step is to measure the mechanical Q of the loudspeaker. Somewhere in the region from 20 to 200 Hz the loudspeaker will give a peak reading on the voltmeter. This is the resonant frequency, f°. We also wish to find the two frequencies either side of f° where the voltmeter reads 70% of the value at f0. We call these two frequencies f1 and f2. Finally, we wish to determine the minimum impedance of the bass loudspeaker, which is the minimum reading on the voltmeter, and is generally a broad minimum occurring at three to ten times f0. We call this frequency f3. What we are interested in here is the ratio of the readings on the voltmeter at f0 and f3.
Figure 2 shows the impedance plot of a 10-inch woofer in a two cubic foot enclosure illustrating the frequencies and measurements sought. Such a plot can be made, if interested, by assuming that the speaker is at its nominal impedance at 1000 Hz. By setting the oscillator to 1000 Hz and adjusting its output amplitude until the voltmeter reads eight millivolts, then the voltmeter reading in millivolts converts directly to ohms impedance. Then it's a simple matter to note the voltmeter reading as frequency is varied (not touching the oscillator level) and then plotting the readings.
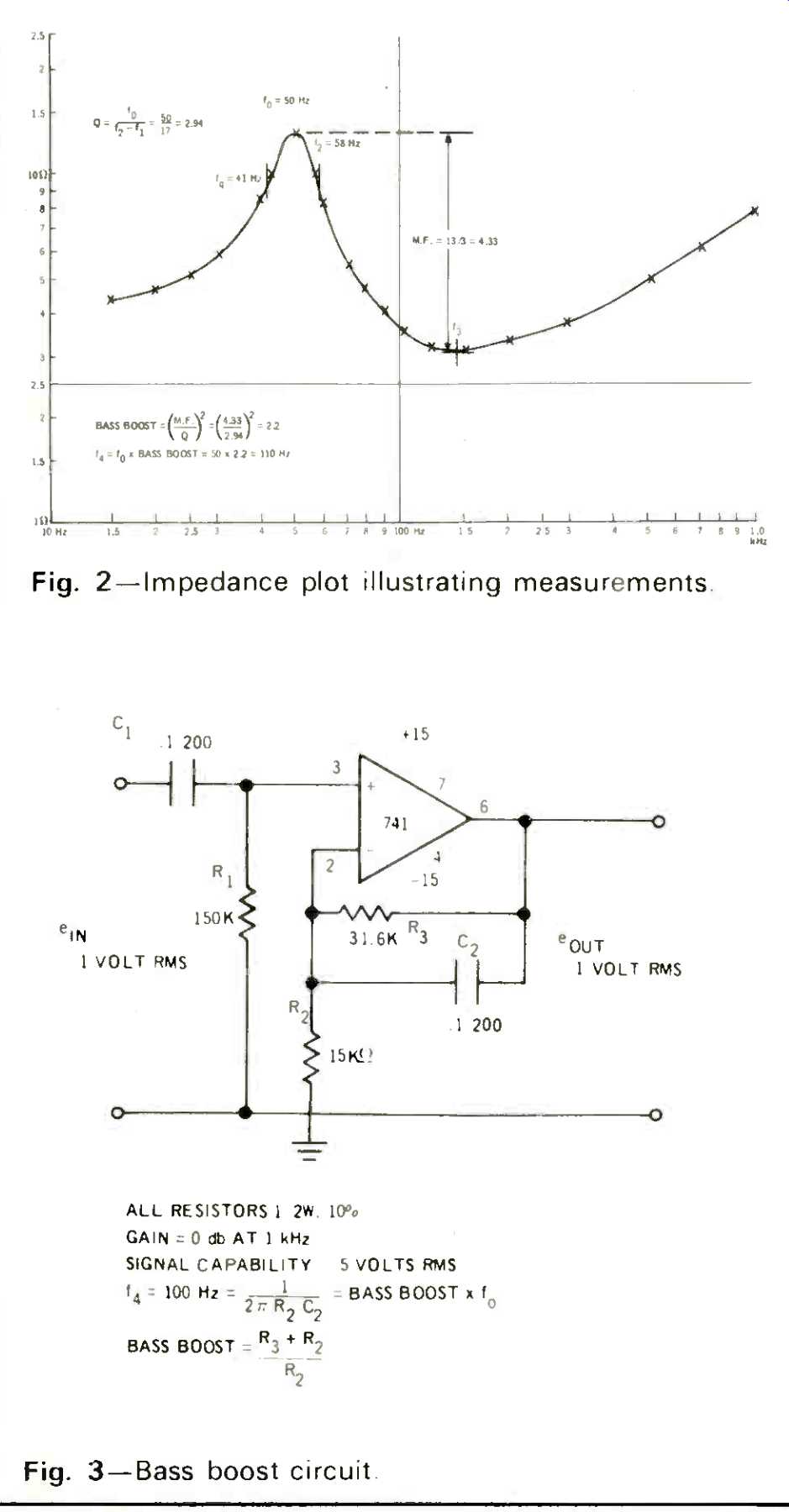
Fig. 2-Impedance plot illustrating measurements.
Fig. 3-Bass boost circuit.
We are now ready for some simple calculations. First we determine the loudspeaker mechanical Q from
(3) Q= f0/f2-f1
Next we determine a number I call the MORE factor. It has no particular meaning to us unless we know a great deal about the design details of the loudspeaker.
(4) MORE factor = M.F. = V0 / V3,
where V0 = the voltmeter reading at f0, and
V3=the voltmeter reading at f3.
Now we come to the crux of the matter and determine the amount of bass boost needed to equalize the loudspeaker.
(5) Bass Boost= ( M.F. / Q)^2
I think it would be wise to explain the above equations. Tilt procedure for determining the mechanical Q is not exact, but it is a simplification of a more precise method', and is accurate enough for loudspeakers of moderate efficiency. The greater the Q of a loudspeaker, the less electrical power we have to furnish it for a given acoustical output at resonance (under steady state conditions). Alas, the greater the mechanical Q of a loudspeaker, the more poorly damped it will be at resonance, and the poorer the transient response. There is not a great deal that can be done by the reader to the speaker to decrease its Q, but we are fortunate in that a speaker with high efficiency will give us more opportunity to electrically damp this resonance'. At any rate the bass response is being increased by this mechanical Q, so we have to know the Q in order to calculate the required bass boost.
But for a Q of one or greater there will be a peak in the impedance curve at resonance. The greater the flux density, the higher the impedance peak. The higher the impedance peak, the more bass boost required to equalize bass response. Thus the MORE factor is a measure of the "peakiness" of the impedance characteristic.
Since the MORE factor is an indication of the bass boost required, and the mechanical Q of the loudspeaker is a measure of the bass boost built into the loudspeaker, we see that the actual bass boost required is some function of the MORE factor divided by the Q. Earlier we saw that the bass loss due to greater efficiency was proportional to 'the square of the relative flux density, thus we have (5) above.
We now know the amount of bass boost required, but we don't know the frequency contour that our bass boost circuit should follow. It the boost is less than twelve decibels at loudspeaker resonance, the single zero, single pole circuit, such as shown in Fig. 3, is adequate. The value of R, in Fig. 3 is shown for the loudspeaker of Fig. 2. The bass boost starts at
(6) f4 = (f0)x(bass boost)
Theoretically, it is possible to equalize the response of a loudspeaker in the frequency range below its resonance, but I have never had much success in so doing. The slope of the equalization curve below speaker resonance is very steep, and the amount of equalization required very large. The practical problems seem greater than the rewards.
Figure 4 shows the results. The bass boost starts at about 105 Hz, is up about eight decibels at 50 Hz, and reaches a peak of 10 decibels at about 30 Hz. Of course, this represents the transmission thru the entire amplifier and not just the bass boost circuit.
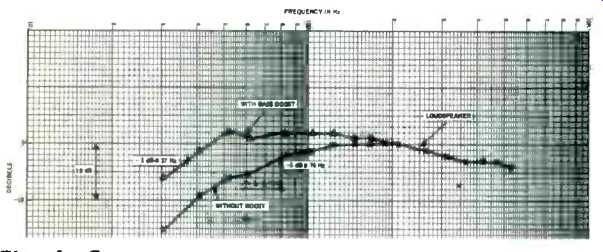
Fig. 4--Freq. response curves.
The before and after effects of the frequency response for the loudspeaker speak for themselves. The measurements were taken with a Hewlett-Packard loudness analyzer in my den. Notice that the bass response has been extended for one octave. The falling off in the 400 Hz region is due to the crossover network for this speaker. The response is smooth and lacks large peaks.
Where, say you, is the catch? Yes, there is one. This technique, that is, the equations as given, is valid only for speakers in sealed enclosures. In fact, the only justification for the approximations made in the analyses is the results of Fig. 4! In the case of other enclosure types, it is difficult to assess the degree to which the enclosure modifies the impedance characteristics in the region near resonance. This brings to mind an observation about enclosures. Most enclosures not only add to the bass by additional radiation, but they also lower the electrical impedance in the vicinity of resonance. This latter effect leads to more current flowing in the loudspeaker which means yet more bass. Several examples are the bass reflex, the auxiliary bass radiator (ABR or drone cone), the labyrinth, and the folded horn. All of these increase the amount of bass by increasing, in some manner, the amount of acoustic radiation. This is represented as an additional resistive component in the mechanical impedance of the loudspeaker, and thus (by equation 2) must lower the electrical impedance. As a matter of fact, I have designed enclosures wherein the port of the bass reflex was designed primarily to control the speaker impedance characteristics. I suspect that some of the aperiodic speaker enclosures on the market now are designed with this same goal.
There you have it. A wrong recognized; a cure proposed; proof that it works. Do I guarantee happiness? No, but if your loudspeaker fits the prescription described above, then you might try bass equalization. I can guarantee more bass!
References
1. Olson, Harry F., Acoustical Engineering, D. Van Nostrand Company. pp. 124-133.
2. Briggs, G.A., Sound Reproduction, Wharfedale Wireless Works, 1953, pp. 110.122.
3. Jordan, EJ., "Loudspeaker Enclosures," Wireless World, January, 1971, pp. 2-6.
4. Briggs, G.A., op. cit.
5. Crawford, Dick, "Another Look at Parallel-Connected Speakers," Audio, November, 1970, pp. 24, 26.
(Audio magazine, Nov. 1973)
Also see:
New Loudspeaker With Extended Bass (Dec. 1974)
= = = =