DITHERING HEIGHTS

Previously, we have explored time sampling, amplitude quantization, and aliasing. We have seen that band-limited sampling is a loss less process, that the problem of aliasing can be largely overcome through an input low-pass filter, and that quantization stubbornly determines the signal-to-error ratio inherent in our digitization system.
If we specify a high sampling rate and a steep filter, sampling and aliasing cease to be meaningful obstacles to the high-fidelity recording and reproduction of audio. But quantization is a different story; that error floor is directly determined by the number of bits in the system.
Although a 16-bit system would yield a theoretical signal-to-error ratio of 98 dB, it is disturbing, at least conceptually, to know that there is still some error down there and that as the signal amplitude decreases to the order of one least-significant bit (LSB)-that is, one quantization increment-an error might even be audible under certain signal conditions.
In any case, quantization always destroys some information, which can create unexpected problems. Let's look at those problems as well as an extremely nifty remedy for quantization error.
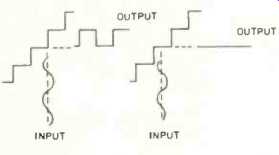
Fig. 1--Without dither, small signals can be reproduced as square waves or
as d.c., depending on whether or not they cross a quantization threshold.
Digital signals are made up of discrete bits. This is a real blessing; it permits us to employ fantastic digital methods for processing and storage.
However, in quantization, the discrete nature of digital and the ensuing amplitude increments can create nonlinearity. Consider the case of a signal with amplitude on the order of one quantization increment (Fig. 1), as proposed by John Vanderkooy and Stanley P. Lipshitz [1]. The signal value would either vary within one increment, resulting in a d.c. signal, or cross back and forth across the increment threshold, resulting in a square-wave output signal. That square wave, created at very low levels, suggests that quantization ultimately acts like a hard limiter; in other words, severe distortion takes place. This quantized fluctuation in the noise floor is perceived as a particularly nasty kind of sound, which is called "granulation noise" because it has been described as a gritty sound. To make matters worse, a square wave is rich in odd harmonics, extending far beyond the Nyquist (half-sampling) frequency; thus, our dear friend aliasing reappears after the anti-aliasing low-pass filter.
Consider the example of a low-level sine wave of 15.333 kHz in a 44-kHz sampling system. The third harmonic creates a 2-kHz component, the fifth harmonic a 32.666-kHz component, the seventh harmonic a 19.333-kHz component, etc. An entire quantization error spectrum has been created, and the anti-aliasing filter is powerless to stop it; these are entirely new components not masked by the original fundamental or its harmonics. If the harmonics are very close to a multiple of the sampling frequency, the beat tones drift through the frequency origin to produce a sound called "bird-singing" or "birdies." Okay, here we are destroying perfectly good information and creating entirely off-the-wall information; even worse, this junk has been euphemistically renamed. Of course, this effect occurs for very low-amplitude input signals; thus, the amplitude of the distortion is also very low. However, it can also happen for higher level input signals of very narrow band. It's a question of the degree of statistical correlation between successive samples. In much the same way that white noise is perceptually benign because successive values of the signal are random (whereas predictable noise signals are more perceptible), we desire noise input signals, and their resulting errors, to be uncorrelated to be least audible.
For broad-band, low-level audio signals, the correlation factor is about 0.5, and for high-level signals it decreases to 0.01. But it rises again for narrow band signals. Quantization error is least perceptible with broad-band audio signals; the correlation is low, and the resulting error is very similar to white noise. But for low-level or narrow-band signals, the error takes on a new, more troubling guise. Yet there is a solution.
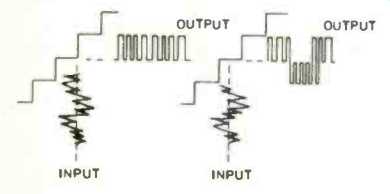
Fig. 2--With dither, the quantized signal is duty-cycle-modulated, reproducing
more of the original signal information without quantization noise.
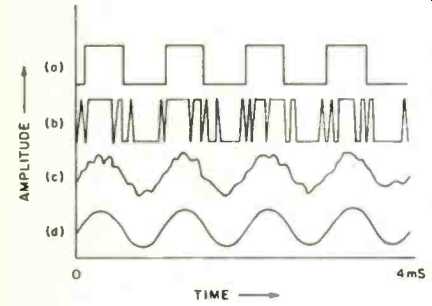
Fig. 3--Small threshold-crossing signal, as output from D/A converter (a)
without dither, (b) with one-LSB dither, (c) after averaging 32 times, and
(d) after averaging 960 times.
A conversion system must suppress any digital quality of its noise. Obviously, the number of bits could be increased, with a resultant decrease in error by 6 dB per bit. This is uneconomical, and it has been estimated that two extra bits would be needed to reduce granulation noise satisfactorily.
An alternative is to add a small amount of analog white noise to the input signal; this noise is referred to as "dither." Dither has been around for a long time (at least since its use in video technology, circa 1950), but it is only now being applied to audio technology.
The point of dither is that a small amount of noise removes the quantization artifacts from a signal-it doesn't mask the artifacts, it removes them.
Let's reconsider our example of a signal crossing a quantization threshold. But this time, let's add a dither signal equal to two quantizing steps.
The result (Fig. 2) is a duty-cycle modulation which still preserves the information of the original signal. As Barry Blesser has pointed out [2], the average value of the quantized signal can move continuously between two levels, and thus the incremental danger of quantization has been alleviated. Audibly, the result is the original sine wave, with added noise. But that is far more desirable than the severely distorting square wave.
Vanderkooy and Lipshitz have proved this hypothesis with the example of a 1-kHz sine wave with a peak to-peak excursion of one LSB, shown in Fig. 3. The familiar square wave is output from the digital-to-analog converter as the limiting action takes place. But when dither with an amplitude of one LSB is added, a duty cycle-modulated waveform results.
While this might still look distinctly digital, its hidden sine-wave information can be revealed when the signal is averaged tens or hundreds of times by our ears. A fairly clean sine wave distinctly emerges. And that averaging technique isn't some kind of trick; rather, it illustrates how the ear will actually perceive the signal.
Our ears are quite good at resolving narrow-band signals below the noise floor because of the averaging properties of the ear's basilar membrane. It behaves like a 1/3-octave filter with a Q of 4, such that the quantization error (which has been given a white-noise character by dither) is averaged out by the ear, and the original narrow-band sine wave is heard without distortion. In other words, dither changes the digital nature of the quantization error into a white noise, and the ear may then resolve signals with levels well below one quantization level.
I think that is a startling and important conclusion: With dither, the resolution of a digitization system is below the least significant bit. By encoding the audio signal with dither to produce modulation of the information, we may later recover that information, even though it might be smaller than the smallest increment of the quantizer.
Exactly how is the dither produced? The mathematical definition for the best kind of dither is, "a noise with rectangular probability density with peak-to-peak amplitude exactly equal to one quantization increment." However, this is a difficult signal to generate, and an ordinary Gaussian (white) noise can be used. In fact, a digital system might not even need a dither circuit, because the residual analog noise in the input stages or the input audio signal itself can act as dither.
The performance price? A degradation of about 1.5 dB in the broad-band noise floor of the digitization system results, an increase which is negligible compared to the signal-to-error ratio inherent in the digital system.
Dither thus represents a unique and unlikely concept. The idea of adding analog noise to a digital system seems a little strange. But, as we have seen, the bottom line is lower distortion and, thus, higher fidelity for the digital system. I think it demonstrates the first stages of maturity in the design of digital audio systems. The nuances of detail are becoming apparent, and the sound just keeps getting better and better.
References:
1. Vanderkooy, John and Stanley P. Lipshitz, "Resolution Below the Least Significant Bit in Digital Audio Systems with Dither," Journal of the Audio Engineering Society, March 1984, pp. 106113.
2. Blesser, Barry, "Digitization of Audio: A Comprehensive Examination of Theory, Implementation, and Current Practice," JAES, Oct. 1978, pp. 739771.
Also see: Philips Oversampling System for Compact Disc Decoding (April 1984)
(adapted from Audio magazine, Nov. 1984; KEN POHLMANN )
= = = =