THE measurement of the characteristics of output transformers is essential, both to transformer and amplifier manufacturers, so that adequate specifications can be laid down for transformers intended to be used in specific amplifier circuits. The necessity for a proper understanding of this is underlined by a common but frequently unsatisfactory practice, not justifiable on a true engineering basis. This specifies the performance of a transformer in terms of a specific production type amplifier, although this qualification may be implied rather than directly stated.
Before the advent of feedback, the frequency response and power-handling capacity, as well as the distortion of an amplifier could be specified in terms of its input and output impedances.
(We shall see later, there can be confusion even about this.) But such specification is no longer possible as soon as any kind of feedback is applied which includes the transformer within the feedback loop. Under these circumstances, the properties of the transformer affect the overall performance of the entire feedback amplifier. This means that transformer design can be quite critical to the amplifier performance and that the use of a wrong transformer design can result in very serious deterioration of amplifier performance or even absolute instability.
Because of this practice the wrong choice of a transformer might not necessarily be an inferior transformer in terms of its own characteristic. It is possible for a superior transformer to result in inferior amplifier performance, if the rest of the amplifier is not designed for such a "good" output transformer. Not only does the transformer contribute a considerable amount to the amplifier's performance, but the transformer's performance, when feed back is included, cannot be completely specified without a knowl […missing p. 120-121…] fed through a standard resistor of value equal to the referred primary impedance. Say the transformer has a ratio of 20 to 1 (turns) to transform impedance by 400 to 1. Then the primary impedance is 400 times the secondary impedance, or 6,400 ohms (Fig. 502) .
But the response of a transformer can deviate considerably, even in non-feedback amplifiers, from that obtained in this circuit.
If the output tube or tubes are of the triode type, the source resistance is usually less than the optimum load resistance. A tube, or tubes, with optimum load (single-ended or plate to plate) of 6,400 ohms would have an effective plate resistance in the region of 2,000 ohms. With this change, the low-frequency response (not the power response) would extend to about one-third the rolloff under standard test. The high-frequency response might vary either way, according to the relative magnitudes of winding capacitance and leakage inductance. But, in almost every instance, it would extend a little further, sometimes perhaps showing peaking which the idealized test would not.
With pentode or tetrode output tubes, the source (effective plate) resistance is many times nominal impedance, and the change in response would be in the opposite direction: the low-frequency response extends to a little less than twice the former cutoff, and the high-frequency response is most likely to be restricted, but with possibility of peaking.
For this reason, output transformers should have the parameters listed or tested that control the low-frequency performance and high-frequency performance, respectively. The transformer can be considered as a contributing component to amplifier response similar to components such as capacitors.
Low-frequency performance
If the transformer is for single-ended output stage operation, low-frequency response is determined by the primary inductance at the operating plate current of the output tube. However, this condition is seldom encountered. Most modern amplifiers use some variety of push-pull operation, so the quiescent plate cur rents (and screen current in the case of various unity-coupled and Ultra-Linear configurations) produce a balanced magnetization of the core.
Under these circumstances the primary inductance is one due to magnetization under ac conditions only. If there is an imbalance of plate currents, due to a slight inaccuracy in the adjustment of balance between tubes, this is usually so small as to be negligible, especially at large output values. It may reduce the low-level inductance of the transformer, but the high-level inductance is practically unaffected.
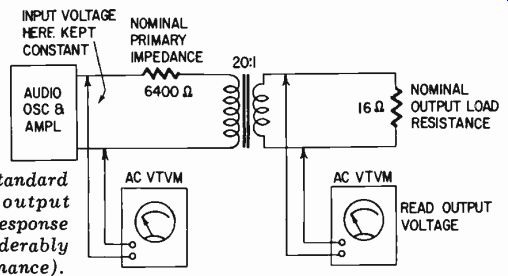
Fig. 502. Basic setup for standard method of measuring output transformer
frequency response (which may differ considerably from its practical performance).
Important to the low-frequency performance of the amplifier is the possible deviation in primary inductance, either with slight imbalance currents in the primary or with the magnitude of ac magnetization due to change in signal level. These inductance values can readily be measured by a modified inductance bridge of the type described in the section on basic measurement. They can be measured at different levels of ac and small dc magnetization.
Two kinds of measurement may be used here. Either the value should exceed a certain minimum under all conditions, or else the inductance must be held between both maximum and minimum limits. The pertinent one will depend upon the way transformer inductance interacts with the rest of the amplifier. There are two schools of thought on the way this should be done. The choice between them should be coupled with the amplifier design approach but, as transformer design is one man's job and amplifier design another's, often this desirable collaboration is lacking.
Low-frequency response should not be confused with low-frequency power-handling capacity, which is controlled by the magnetizing current the transformer draws at low frequencies.
But both must be considered together in determining how low-frequency transformer performance should be measured.
Sometimes it is stated that distortion occurs when the transformer magnetizing current runs into the saturation region. With modern feedback amplifiers, this is not always true. Often the source resistance of the amplifier is reduced by feedback to such a low value that a magnetizing current comparable with the load current can be drawn before appreciable increase in distortion is noticed, at least when measuring the performance into either open circuit or a resistance load.
The addition of the magnetizing-current dynamic loop to the resistance-load dynamic line produces a trapezoidal form of load loop. This permits the transformer to be operated at a higher maximum flux density at the low-frequency limit and still give satisfactory output under specified amplifier operating conditions.
If this feature is used in amplifier design, there are two ways of specifying the magnetizing current at the low-frequency limit and maximum output. One gives the maximum current peak, which involves the use of a peak-current indication to measure it, while the other specifies the maximum magnetizing current as measured on an ac meter of specified characteristics and the harmonic component of this magnetizing current. This can be measured by a standard resistance connected in series with the primary when the full voltage is applied to the transformer at lowest frequency. The resistance value is such that the expected magnetizing current will produce a voltage drop not more than about 1/20 of the working primary voltage. This voltage is then used to calculate the current value. Its harmonic component is measured by a regular harmonic meter of a circuit similar to Fig. 317. (See Fig. 503). Either method sensibly achieves the same objective and it is principally a matter of convenience as to which form of specification is used.
This approach to the problem may be questionable when it comes to deciding the contribution of the transformer to amplifier performance at maximum output and lowest frequency. It may result in satisfactory performance into a resistance load, but give serious limitation of power when the load contains inductive reactance.
When the transformer is designed to meet a minimum inductance by using a laminated (not gapped) core, so that operation at low-frequency maximum level approaches saturation of the core the approach used in Fig. 503 is useful. With the other approach, which controls inductance within limits by gapping the core, saturation is not usually a limitation, because a greater number of turns and a larger core size are needed to achieve adequate inductance.
In the second case measurement of inductance using a modified Hay bridge (Fig. 316) with the required primary current flowing (unless it is push-pull operation) is all that is needed to check the low-frequency end. If adequate inductance has been provided to avoid reducing the output from the tubes at the lowest frequencies, the maximum power-handling requirement will automatically be met. If not, the fault is in the value of inductance chosen for the particular output tubes.
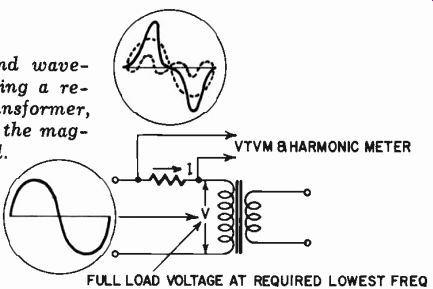
Fig. 503. Magnetizing current and wave form can be measured by inserting a
resistance in series with the transformer, such that the voltage drop due to
the magnetizing current is small.
High-frequency performance
For high-frequency response two characteristics of an output transformer contribute to the overall effect; leakage inductance and winding capacitances. According to the method of operation used, the leakage inductance will be that between whole primary and secondary for class A, or between each half primary and secondary for class B. The winding capacitance is particularly that of the primary winding, since this has the highest impedance.
As most modern amplifiers utilize a relatively low plate-to-plate impedance, primary-winding capacitance is not usually a serious feature in amplifier design. Its effect on performance is marginal and often insufficient to warrant attention in the transformer performance specification.
Leakage inductance, however, can perform an important role in the stability characteristic of the amplifier. Sometimes it may not be important with a resistance load, but can be the controlling factor in approaching instability when the amplifier is operated with an inductive or capacitive load, as when driving an electro static tweeter.
Before the advent of feedback amplifiers, leakage inductance in combination with primary capacitance were the sole controlling factors for high-frequency response. Any combination of these two values that would result in an acceptable high-frequency response with the operating impedances, primary plate resistance and secondary load resistance would be considered acceptable for a particular amplifier. Thus transformers with different combinations of leakage inductance and winding capacitance, with the same circuit resistances, could each be acceptable (Fig. 504). This shows that in a practical circuit, three combinations of leakage inductance and winding capacitance (at least) are acceptable, while two of them, widely divergent, give identical response. This is not the standard test circuit, in which different possible combinations would prevail.
In feedback amplifiers, these are not the only factors that control the overall frequency response when the transformer is included in the amplifier feedback. There is also the combined effect of the time constants produced by the leakage inductance and primary capacitance with the associated circuit resistances, in combination with the time constants of the interstage couplings in the earlier part of the amplifier. Serious deviation beyond design allowed variation in any can result in deterioration of amplifier performance and possibly even in instability under certain circumstances. Consequently, it is more important to specify and measure within limits values of leakage inductance and winding capacitance, both ways if necessary, or as minimum or maximum values where these form the controlling limitations.
Besides interfering with correct feedback operation, incorrect transformer design can cause spurious effects. These have frequently been specified in terms of overall performance of the amplifier with the transformer connected in it. Often it is implied that the transformer causes notches in the waveform or peaks and valleys in response at some high frequency.
Usually a transformer measured from whole primary to whole secondary produces no such deviation in waveform or frequency response. Deviation in waveform can be due to a defect such as shorted turns; deviation in response to very poor winding layout.
These types of distortion usually occur only when the transformer is operated in a push-pull amplifier, especially one using some special cross-coupled pentode circuit or Ultra-Linear taps, and when sufficient care has not been given to proper electrical balance.
The percentage tapping (in the case of Ultra-Linear) varies at the high frequencies so the tubes do not maintain a linear characteristic. Also, phase deviation that accompanies such variation in magnitude can cause nonlinear operating conditions between pairs of a push-pull output stage so as to cause distortion of quite a serious nature. This is not due to the transformer's internal non-
linearity, but to its causing the tubes to operate under conditions widely deviant from their specifications.
The same kind of thing can also happen with class-B or even class-AB operation, particularly when the output tubes are pent odes. At some point on higher-frequency waveforms, the different phase shifts the transformer produces in plate loading cause them to work momentarily push-push, instead of push-pull, resulting in a form of frequency doubling.
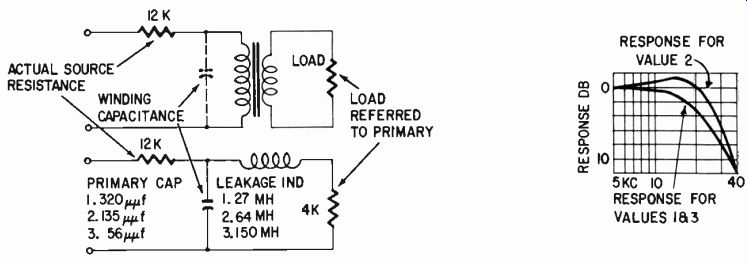
Fig. 504. In amplifiers without feedback, a wide variety of combinations of
leakage inductance and winding capacitance might be acceptable.
Consequently, we need some means of specifying and measuring output transformer operation that will control this situation and eliminate the possibility of such deviations when the transformer is connected into a practical amplifier. The leakage inductance of different components of the primary winding to various other components can be specified. But this, unfortunately, is not satisfactory unless it is specified in combination with the major leakage inductance components.
For example, if the leakage inductance from one half primary to the secondary is 10 millihenries, referred to that half primary, and the leakage inductance from the same plate tapping to the corresponding screen tapping is 2 millihenries referred to the same section of plate winding, the transformer will probably be satisfactory for Ultra-Linear operation. The coupling is maintained relatively tight until the leakage inductance between primary and secondary loosens the coupling as a major amplifier.
Such a transformer could be specified as having a maximum leakage inductance from half primary to secondary of 10 milli-henries and a maximum leakage inductance of 2 millihenries from plate to screen tap of the same winding. However, such a specification would be adequately met by a transformer that has a measured leakage inductance of 2 millihenries from plate to screen tap and of only 2 millihenries or so from plate to secondary. This would not be a satisfactory transformer because now the coupling between plate and screen is not adequate up to the highest frequency the transformer can handle as an energy transfer device.
The important feature of a design in this case is not that the leakage inductance between plate and screen referred to the plate winding should be less than 2 millihenries, but that it should be less than a specified fraction of the leakage inductance between the plate and secondary winding from which the overall feedback is taken.
This, then, is the way the transformer should be specified and measured: The leakage inductance between half the primary and the secondary should not be more than 10 millihenries (in this example). And the leakage inductance between the same half primary winding and its screen tap, referred to the whole winding, should be not more than one-fourth of the leakage inductance to the secondary. This has been called "coupling factor," but should really be spelled out to avoid possible ambiguity. If primary to secondary is 8 millihenries, 2 millihenries to the tap is satisfactory. If it is less than 8 millihenries, the leakage to the tap must be proportionately smaller.
Similarly, in most push-pull stages, the leakage inductance between halves should be specified in terms of the leakage inductance between primary and secondary, rather than as an absolute maxi mum value. The specification of leakage inductance between primary and secondary, either half primary and whole secondary or between the two whole windings, should be controlled to specified values in the interest of overall stability of the amplifier over the required loading range.
Such a method of specification and basis for measurement is obviously more satisfactory than the more common method of specifying the transformer's performance in a specific amplifier.
It obviates the problems that arise when certain transformers fail to perform to specifications in certain units of the ``same" proto type amplifier. In short, it enables the transformer to be specified in the same kind of terms used for tubes and other components in an amplifier, so it is readily possible to determine what it is that causes an amplifier to fail in meeting its specifications.
Leakage inductance between primary and secondary can be measured by short-circuiting one winding and measuring the inductance at the other winding, to which the value is referred, by a suitable inductance bridge (Fig. 505).
An alternative method consists of finding the leakage inductance by resonance. The signal from an audio oscillator is injected from a low-impedance (preferably near zero) source provided by a suitable power amplifier into one winding and applying the resonant capacitance to the other winding-the one to which the leakage inductance is required to be referred (Fig. 506). This method has two advantages: (1) with slight adaptation, it can also be used to determine the primary capacitance; (2) it is simple to apply to the relative values discussed.
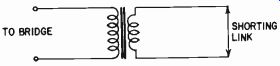
Fig. 505. Leakage inductance can be measured by shorting one winding (right)
and measuring the inductance at the terminals of the other (left). Leakage
inductance between these two windings is referred to the winding at which it
is measured.
If the amplified audio oscillator signal is injected in the secondary winding, to find the primary-to-secondary leakage inductance referred to the primary, the capacitance is connected across the primary and the resonant frequency for different values of capacitance is measured. This resonance is due to the leakage inductance resonating with the total capacitance formed across the primary by the additional external capacitance with the primary's own self-capacitance.
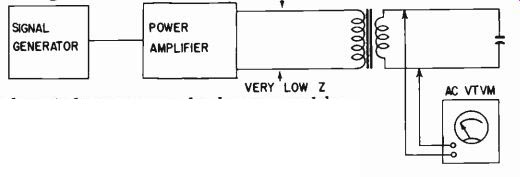
Fig. 506. Leakage inductance can also be measured by resonance, inserting
a signal at one winding (left) and resonating the other (right). The leakage
inductance obtained is referred to the winding to which the capacitance is
connected (right).
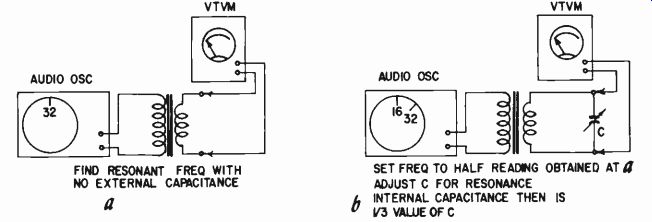
Fig. 507. Checking winding capacitance and leakage inductance. After calculating
the internal winding capacitance, the leakage inductance is obtained from the
resonant frequencies used.
First, a reading should be taken of the natural resonance of the transformer without external capacitance. Then external capacitance should be added, just sufficient to halve the resonant frequency. This external capacitance will be just three times the effective self-capacitance of the winding (Fig. 507). From this the internal capacitance can be calculated and the leakage inductance found from this formula:
L = 1/4/pi^2f^2C
Suppose, for example, the self-resonance is 38 kc and an additional capacitance of 360 uuf is needed to bring this down to 19 kc.
Then the self-capacitance is 1/3 of 360 uuf, or 120 uuf. And leak age inductance is given by (above formula applied)
= 0.147 h, or 147 mh
In making these measurements, the points on the windings that normally are at ground, B-plus or some potential normally decoupled to ground, should be connected together so the distribution of alternating voltages within the transformer is correct.
Changes in effective ground points can modify the effective self capacitance of windings, although the effective leakage inductance between windings is unmodified.
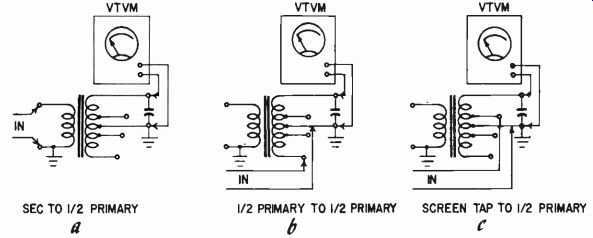
Fig. 508. Checking relative leakage inductance ref erred to the same section
of winding (in this case the upper half of the primary) from other parts of
the transformer.
If all leakage inductances and capacitances are to be referred to either one-half or the whole primary winding, the extra external capacitances can be connected to these windings in all cases. But the input can be connected at different points, according to the specific leakage inductance being measured.
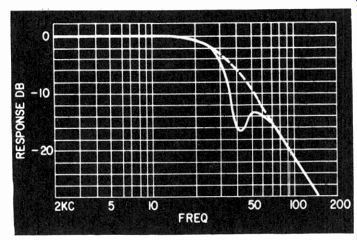
Fig. 509: Sometimes unevenly distributed effects can cause a notch in the
transformer's transfer response, after it has started rolling off.
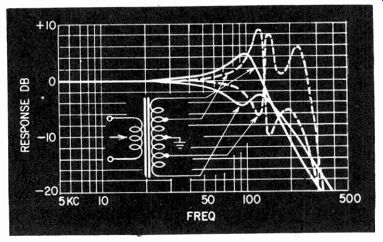
Fig. 510. Some of the peculiar response curves obtainable with an Ultra-Linear
transformer of poor design (only frequency response curves shown-the phase
curves are much more involved).
For example, to measure the secondary to-half-primary leakage inductance, the additional capacitance is connected across one-half the primary and the signal injected in the secondary. To measure leakage inductance between half primaries, the signal is injected in one-half of the primary and the additional capacitance connected across the other. To measure leakage inductance between the screen tap and plate of the same half primary, the signal is injected in the screen tap and the additional capacitance connected between plate and the B-plus tap. These conditions are illustrated in Fig. 508.
When relative coupling is the important factor, this can be determined from the relative values of capacitance that tune to the same frequency when the input is connected to the tap in question. If the capacitance is five times, the leakage inductance referred to that winding is one-fifth. To check that the coupling factor meets specified requirements, the capacitance can be changed by the minimum acceptable factor, and then a recheck made that the resonance is not lower than for the whole winding.
If it goes higher, it is within limits.
An advantage of this method of measurement is that a vtvm can be used as the indicating device. A vtvm will usually have a very high input impedance and low input capacitance and thus is suitable for connecting in parallel with the additional external capacitance. This point is one where resonance is marked by a voltage maximum and thus is easy to measure without interposing any additional resistance between the generator source and the input winding.
Leakage inductance between windings is not subject to variation like primary inductance, either with dc magnetization or with different values of signal level. Neither does it change with frequency. Consequently, the methods of measurement just set out can produce quite accurate results, provided the leakage inductances and self-capacitances are not so complicated that it becomes impossible to measure one without the interference of various other components in the same transformer. Even then there may be a "kink" in the rolloff curve (Fig. 509).
In some instances this occurs due to quite violent interaction of various internal self-resonances of the transformer. These disappear (if at all) only when the full transformer is loaded between the whole windings. A method of detecting this characteristic is to inject signals on the secondary side of the transformer and measure the output voltage as a frequency characteristic from the different taps of the primary. Typical results taken in this way on a poor transformer are shown in Fig. 510. With such a transformer, using the measurement techniques just described, it is impossible to get a consistent reading of leakage inductance be tween different sections of the primary. The interfering resonances make any one apparent value of leakage inductance deviate in the most inconsistent and impossible manner.
Recommended Reading
1. "The Use of A. F. Transformers." Norman Price Publishers Ltd., London, 1953.
2. "Leakage Inductance," Electronic Engineering, April, 1949.
3. "Winding Capacitance," Electronic Engineering, November, 1949.
4. "Measuring Up an Audio Transformer," Audio Engineering, November, 1952.
5. "Making the Best of an Audio Transformer," Audio Engineering, January, 1953.
6. "Audio Transformers Can Be Good," Audio, May, 1956.
7. "Output Transformer Design," Audio, September, 1956.
8. "How an Output Transformer Causes Distortion," Audio, February and March, 1957.
9. "Electrical Adjustment in Fitting a New Output Transformer," Audio, April, 1957.
*In all instances, the author is Norman H. Crowhurst.