Hofmann's Iron Law--a curiously useful way of looking at the low frequency performance of loudspeakers...
By HENRY KLOSS [Advent, Inc. ]
THERE HAS always been a certain willingness to suspend both disbelief and rationality in the discussion of loudspeakers, and for the most part it doesn't really harm anything. People tend to wind up buying their speaker systems on fairly reasonable, pragmatic grounds, and aren't likely to be disturbed by the adman/ salesman/theoretician who holds that it takes a round speaker to yield "round sound" or a speaker system the size and shape of a bass viol to reproduce the sound of one. We do, of course, see some nicely rounded and bass-viol-sized speakers in stores as a result, but the relatively few people who buy them probably have their reasons and can't be considered the worse for it.
Still, there are times when a loudspeaker designer has pangs and longs to sneak a bit more enlightenment into the discussion-even if it makes clear, as the following may, that just about anyone might design a good-to-wonderful low-frequency loudspeaker system by following rules that are both few and simple.
So, then, a catharsis for a speaker designer. And an attempt at some new and hopefully useful ways of looking at the low-frequency performance of the kind of speaker system that has such wide acceptance as a high-performance device. That, of course, is the sealed box, acoustic-suspension system now made (in various adjectival forms) by just about every speaker manufacturer.
We won't argue the possibility of a better design somewhere in some better world, but simply proceed with the knowledge of the present design's sublime usefulness in this one.
One of the delightful things about the sealed-box, acoustic-suspension, single-degree-of-freedom speaker is that it's a quite simple system, with an attendant lack of eccentricity. The parameters that decide its behavior are there all the time, and you can vary them for different objectives-as we will be discussing-with known results. You don't wind up with egregious behavior in some performance area as a result of some apparently harmless change, and you don't then have to waste time looking for some "patch" that may itself have some strange effect.
Which means, of course, that low-frequency performance can't be determined by the sheer weight of money or the designer's ingenuity, since the rules stay the same whatever the designer's resources. But while this may disturb those designers who like to think they can buy their way out of a design limitation, or those who think that a particular kind of voice coil or cone material or construction has a certain mystique, it's very nice for all the rest of us. And it does leave the designer free to make some choices, hopefully enlightened, of what to emphasize and what not to emphasize, since total subjective effect or suitability isn't as nicely predictable as are curves and such.
So, while the behavior at low frequencies of a certain sort of speaker isn't the most metaphorically exciting subject for an article, it does give us a chance for a close look at some reasonably interesting things that can be stated both simply and rigorously. Nothing new, really, except perhaps a new window on reality.
What I propose to do is being with a speaker design of known excellence and discuss its basic and completely dependable interrelationships: What happens to performance from various physical changes, what physical changes are needed for a specific performance objective. The assumptions (forgetting about the vital question of your interest in all this) are:
--That we are talking about the sealed or effectively sealed speaker system. (Some latter-day ported systems are essentially sealed boxes that follow the rules we will be discussing.)
--That the speaker derives all damping from its voice coil moving in the field of its magnetic structure and is used with an amplifier of modern high damping-factor (4 or above) design.
--That the amplifier is not tailored in frequency response to a particular speaker.
--That we aren't making any judgment on how much sound must be produced, but working within known and accepted parameters for average to demanding home use.
--That we aren't after the discovery or definition of one "ideal" loudspeaker, but discussing possibly useful variations within an area of known goodness (or, if you prefer, excellence).
The discussion which follows will be different from the usual presentations in an important way. We shall deal only with those parameters whose manipulations are at the discretion of a designer.
By eschewing the inclusion in our statements of such quantities as the density of air, the velocity of sound, the value of 2 pi r, and other constants that are constant for all speakers in this group, we are forbidden to make statements of equality in connecting physical parameters with performance characteristics. We can, and shall, make perfectly rigorous statements of proportionality which will permit us to precisely predict the performance of any new speaker as a function of the change in parameters of a prototype speaker.
If we are told, and we should certainly readily believe, that the weight of a pile of jelly beans is proportional to the number of jelly beans, we should be quite confident that if we multiply the number of jelly beans by 1.2, the total weight will increase by 1.2. Note that we did not have to know how much a jelly bean weighed. If our job is to manipulate the number of jelly beans and then keep track of total weight, we shouldn't concern ourselves with those things (constants, i.e., weight of individual jelly beans) over which we have no control.
If we are really dedicated to our job of getting at the essential truth, we can even readily accept the fact that these jelly beans are in a fixed size container whose weight does not appreciably disturb the relationship between number and weight of jelly beans over the range in which we are interested (see assumptions above). The whole presentation is directed toward an attempt to make a powerful final statement that connects together those several characteristics which directly affect the value of a loudspeaker to a user.
A good place to begin is the area of greatest comfort to any speaker designer: The frequency range from 800 Hz down to the point below 150 Hz where variations in low frequency curves may begin to be visibly and audibly significant. What is of such comfort about the 150800 Hz range, as has been stated elsewhere many times, is that it's "flat" by nature (1). Over that frequency range, the speaker's velocity and hence output is controlled by the mass of its moving system. Assuming good design as we are throughout, in this case of the cone, there is ideal piston operation. Cone velocity goes up as frequency goes down, doubling for each halving of frequency (a fact with which Mr. Klipsch apparently likes to frighten small children) to coincide nicely with the realities of decreasing radiation resistance. Output can be calculated precisely at any point in the range as the square of cone velocity times the square of the area times some constants. No trickery is needed to make it come true nor are any special cone materials (a wide variety of thoroughly conventional materials and compositions will do nicely).
But things change as the bass resonant frequency of the system is approached. In a proper closed-box system, output beings to drop at a point somewhere above resonance (we'll be more specific in a moment), drops more at resonance, and begins to roll off fairly sharply (12 dB/octave) somewhere below that as stiffness reactance halves the cone velocity for each lower octave. If benign nature seemed to rule in the 150-800 Hz range, the designer takes responsibility now for everything, including (a) the shape of the roll-off, resonance curve, (b) where it begins laterally on the frequency scale, and (c) where the curve and the reasonably straight line between 150 and 800 Hz show up on the vertical scale of absolute power output.
He is responsible, all right, but the rules are the rules.
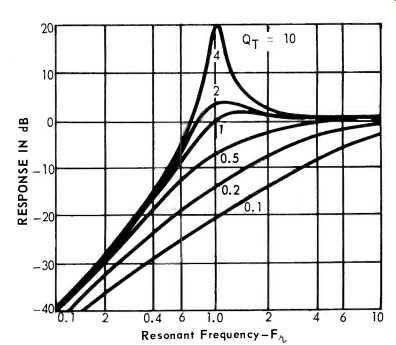
Fig. 1--Frequency response versus Q.
The shape of the frequency response curve of every speaker of the type we are discussing will inevitably correspond to one of the family of these familiar universal resonance curves. We can construct a graph with explicit labels for x and y axes which completely describes the speaker's performance quantitatively if we know three performance characteristics:
A. Efficiency, or the amount of output in the "flat" region for a given power input,
B. Resonant frequency, or the actual frequency at point labeled FR on curve, and
C. Which shape of curve.
Now, there are four, and only four physical parameters that in turn set those three performance characteristics:
1. A = area of cone,
2. M = mass of moving system, (cone and voice coil largely),
3. Motor = "strength" of the magnet voice coil motor (2), and
4. V = volume of air enclosed in sealed box.
Let us relate physical parameters to performance characteristics:
A. Efficiency = A2/M2 x Motor;
B. Resonant frequency, which we shall call:
Fr = __/ stiffness/mass
Stiffness here is assumed to be solely due to cone area pressing against a small enclosed volume of air and as such is approximately equal to A^2/V so that:
Fr = __/A^2/VM
C. Shape of curve is actually determined by the "Q" of system at resonant frequency. The relating of QFR to the physical parameters is a somewhat messy expression, involves all four of those a parameters and does not readily permit a feel for the physical situation. We would like now to introduce a different term which relates to shape of curve that makes it much easier to figure out the new performance of a speaker when any one physical parameter is changed. Use of this new term will then lead us to a way to make a powerful and simple statement. We shall also relate this new term to Q_FR as we must be able to. They are both, after all, equally legitimate ways to describe the shape of curve.
Short Digression
Imagine a loudspeaker with no stiffness at all, that is a resonant frequency at 0 Hz.
Now, let us examine the output as we move down in frequency. We know there is a region of constant output and might expect this to continue to indefinitely low frequencies; we shall certainly never get to the 12 dB octave slope caused by stiffness reactance.
Since this loudspeaker must have a motor (some volume of conductor in a magnetic field, here assumed to be fed from a low impedance), there must be some damping force, which, no matter how small, will at some low frequency equal the continually decreasing mass reactance and cause the output to decrease by 3 dB. We shall find it convenient to express the very important relationship between mass reactance (tendency for velocity to increase with lower frequency) and the resistive damping force (tendency for velocity to remain constant) as the frequency at which the two become equal. This we shall call the damping frequency. A stronger motor, i.e., more damping, will cause this frequency to be higher; a heavier moving system, more mass reactant, will cause this frequency to be lower.
We can see that this quantity is in no way dependent on area of cone or volume of enclosure, but is just a way of describing the relative influence on the velocity of the cone at any frequency of the mass of the moving system and of strength of the motor, and one can readily see that damping frequency which we shall call FD approximately equals motor divided by mass.
To gain familiarity with damping frequency, FD, imagine a speaker with FD at 240 cps and resonant frequency, FR, at 60 cps. If we examine the shape of the frequency response curve going down in frequency from the flat region, we are told that already at 240 cps the damping force is significant compared to the mass reactance in determining cone velocity, and the output is thus below the flat region and shall be even lower by the time we move down to 60 cps.
Now take a speaker with FD 15 cps and FR 60 cps. As we move down in frequency from the flat region, we see that when we pet to the resonant frequency, the "damping force" is still not a strong contributor to determining cone velocity and, since mass reactance at this frequency (by definition) is cancelled by stiffness reactance, velocity, and hence response, is allowed to rise appreciably.
One more example: A speaker with FD = 60 cps, FR = 60 cps. Remembering our definition of damping frequency, this speaker would have been down in response by 3 dB if there were no stiffness at all, i.e., resonant frequency = 0. Because resonant frequency is 60 cps, the mass reactance, which is equal to "damping force," is cancelled by stiffness reactance and the response is allowed to double, i.e., rise 3B to the level of the "flat" region. From this fact you can readily pick out the appropriate curve, namely QFR = 1. (See Fig. 1) In fact, the curve fitting the other two speakers examined can be readily found by making use of the relationship between QFR and Fn that
QFR= FR/FD.
This is just a consequence of the way we have defined Fn. Our first speaker is thus seen to have the curve corresponding to QFR = .25 and speaker number 2 has QFR = 4. One might complain that at the beginning we should have just said that FD =FR/QFR but that would have denied us the chance to get some physical "feel" for FD and to see why logically it is approximately equal to motor divided by mass.
So our digression has given us a way to express performance characteristic C in a slightly indirect way by specifying FD.
To then find shape of curve we note ratio of resonant frequency to damping frequency which gives us QFR to enable us to assign the proper curve. So for C we then write damping frequency approximately equals motor divided by mass.
This relating of physical parameters to performance characteristics makes it quite easy to readily identify all changes in performance when any one of the four physical parameters are varied.
One can quickly go through the four examples:
1. Increase area: increase efficiency, increase FR. 2. Increase volume: decrease FR. 3. Increase mass: decrease FR, decrease efficiency, decrease damping frequency (QFR goes up). 4. Increase motor: increase efficiency, increase damping frequency (QFR goes down).
This is quite handy for a speaker designer but the interrelationship of a different set of characteristics has much broader importance. The loudspeaker buyer-listener is not, or should not be concerned with mass of system, area of cone, or strength of motor. None of these individually are separately discernible to a buyer-listener as being proper or improper. I believe we can identify three outstanding characteristics that truly determine the value of a speaker to user (remembering that we are here concerned solely with low frequency performance). This value, after all, at least here, is the most proper concern. Our intended service here is to show how these value characteristics are rigorously tied together in a very simple way.
The value characteristics are:
1. Volume of enclosure. The smaller the better. This strongly affects the utility of the speaker with respect to allowing optimum placement and even more strongly affects price.
2. Efficiency. The higher the better.
Total loudness for given electrical power.
3. Low frequency response performance, which we have shown to be defined by: 3a. resonant frequency. The lower the better. 3b. damping frequency. The lower the better.
(Assuming we are discussing a properly designed high performance speaker in which the motor, for sake of reasonable efficiency, has been increased beyond the point that frequency response alone would like, i.e., the speaker is over damped.) It turns out that these four quantities are closely interdependent. The exact statement of this interdependence turns out to be very pleasing for its simplicity, which is the reward that should be expected for the effort to acquire this new conceptual tool of damping frequency.
Let us again express each of these "user value characteristics" in terms of their dependence on physical parameters:
1. Volume ^ volume
2. Efficiency ^ A2/M2 x Motor 3a. Fr ^ JA2/MV 3b.Fd ^ Motor/M
Now just a few lines of old math eighth grade algebra. From 3a, squaring each side we have:
F A2/MV or A2 ^F1MV
Let us restate efficiency, substituting for A2 as:
Efficiency ^ Fr MV Motor/M2 = Fr V Motor/M
But we recognize:
Motor/M as Fd
So we finally get:
Efficiency ^ Fr FdV
If one wants to consider only a given shape of curve, that is a given QFR, we can then express FD as some factor of FR and further simplify our law to:
Efficiency ^ Fr V
These then are the quantitative expressions of what I have come to call Hofmann's Iron Law(3) prescribing the amount and direction of change that must occur in one or two or three of the remaining terms when any one is changed.
Note that this law does not say what happens to any one term as a given term is changed, that is, for instance we are not told how efficiency changes if the volume changes. (In fact, it doesn't change at all.)
Once it is decided to vary any term in this statement, it is up to the designer to rearrange physical parameters both to accomplish this change and properly apportion the necessarily resulting change in the other terms to make the most acceptable "new" speaker.
This iron law which shows difficult and frustrating constraints facing an engineer (but apparently not every advertising department) can also console one that the "improvement" one can make over an already properly designed speaker must be nil, independent of his resources or intelligence. A very constructive use can be made of this law by noting not only what it requires but what it may allow. Physical laws are not inherently malevolent, after all. For instance, we might observe that one could start with a loudspeaker of truly distinguished low frequency performance and keeping FR and FD the same have exactly that same shape of curve in one half the volume at 3 dB less efficiency. Arguing the possible value of such a special speaker is outside the scope of this article; our only intent here is to prove that it is possible and even indicate how the physical parameters should be juggled to achieve the result.
1. Technical articles back to Rice and Kellogg's of almost 50 years ago have described this natural occurrence of Ideal flat behavior. More recently Audio covered the subject well in the March 1970 loudspeaker issue. Our treatise assumes a vague-to working familiarity with the content of such tracts. We are just offering a statement of consequences of the facts which have been well reported.
2. This parameter, which occurs in the expression for efficiency (establishing the force delivered to the moving system as a function of electrical power input) is the same parameter that determines the resistance offered to the moving system by a shorted coil in a magnetic field which, although it is an impedance (real), we are calling "damping force." The expression for strength of motor in terms of physical parameters is approximately magnetic field times volume of conductor. Since those terms always occur together in describing performance characteristics, we shall carry them along, describing them solely as "motor." The designer can then decide how he apportions values between magnetic field and volume of conductor to get the required motor and then decide how he subdivides this volume of conductor to get his desired impedance level. To drag along length of conductor, etc., through all which follows would really obscure the picture.
3. Dr. J. Anton Hofmann first introduced the term "damping frequency" about 16 years ago when the author was struggling with the design of the first of this then-new type of loudspeaker, the AR-1. The use of the term as a manipulative device and, more importantly, the expression of the interrelationships of the "value in use" characteristics that the use of this term revealed were a powerful tool that permitted the designer easily to systematize the design of low frequency loudspeakers. Dr. Hofmann later lent his Initial to another loudspeaker company and subsequently has become treasurer and chief-enforcer of-rigor of Advent Corporation.
(adapted from Audio magazine, Mar. 1971)
Also see:
Tractrix Horns--Improved Imaging and Phasing (Mar. 1991)
The Why and How of Horn Loudspeakers (Mar. 1971)
= = = =