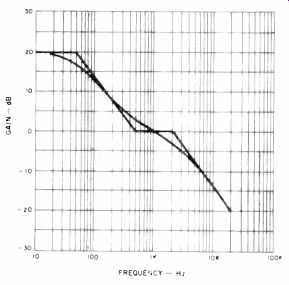
Present methods of measuring signal-to-noise (S/N) ratios do not represent the true noise performance of phono preamps under real operating conditions. Noise measurements with the input shorted are only a measure of the preamp noise voltage, ignoring the two other noise sources, the preamp current noise and the noise of the phono cartridge.
Modern phono preamps have typical S/ N ratios in the 70 dB range (below 2mV @ 1 kHz) which corresponds to an input noise voltage of 0.64 µV which looks impressive but is quite meaningless. The noise of the cartridge 1 and input network is typically greater than the preamp noise voltage, ultimately limiting S/ N ratios, and this must be considered when specifying preamplifier noise performance. A method of analyzing the noise of complex networks will be presented and then used in an example problem.
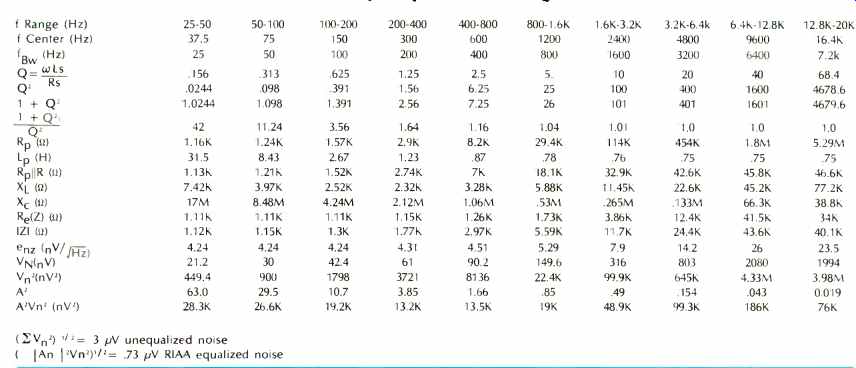
Table 1--Summary of phono cartridge calculations
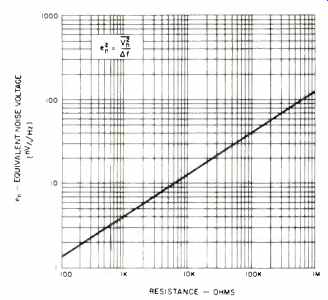
Fig. 1--Thermal noise voltage vs. resistance.
Review of Noise Basics
The noise of a passive network is thermal, generated by the real part of the complex impedance, as given by Nyquist's relation:

The total noise voltage over a frequency band can be readily calculated if it is white noise (i.e., Re (Z) is frequency independent). This is not the case with phono cartridges or most real world noise problems.
Rapidly changing cartridge network impedance and the RIAA equalization of the preamplifier combine to complicate the issue. The total input noise in a non-ideal case can be calculated by breaking the noise spectrum into several small bands where the noise is nearly white and calculating the noise of each band.
The total input noise is the rms sum of the noise in each of the bands N1 ... Nn.
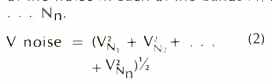
This expression does not take into account gain variations of the pre amp which will also change the character of the noise at the preamp output. By reflecting the RIAA equalization to the preamp input and normalizing the gain to 0 dB at 1 kHz, the equalized cartridge noise may then be calculated.
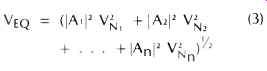
Where VEQ =Equalized preamp input noise and IAn1 = Magnitude of the equalize gain at the center of each noise band (V/ V).
Cartridge Impedance
The simplified lumped model of a phono cartridge consists of a series inductance and resistance shunted by a small capacitor. Each cartridge has a recommended load consisting of a specified shunt resistance and capacitor. A model for the cartridge and preamp input network is shown in Fig. 3.
This seemingly simple circuit is quite formidable to analyze and needs further simplification.
Through the use of Q equations', a series L-R is transformed to a parallel L-R, as shown in Fig. 4.
The impedance relations for this network are:
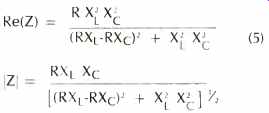
Example
Calculation of the RIAA equalized phono input noise is done using equations (1)-(5). Center frequencies and frequency bands must be chosen: values of RD, Lp, Re(Z), IZI, and noise calculated for each band, then summed for the total noise.
Octave bandwidths starting at 25 Hz will be adequate for approximating the noise.
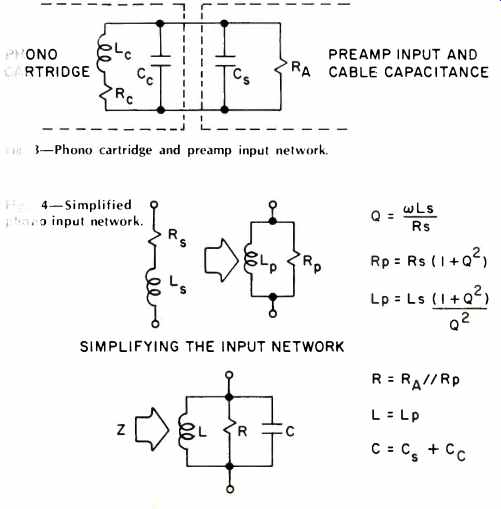
Fig. 3--Phono cartridge and preamp input network. Fig. 4--Simplified phono input
network.
An ADC-27 phono cartridge is used in this example, loaded with C = 250 pF and RA-47 kilohms as specified by the manufacturer, with cartridge constants of Rs = 1.13 kilohms and Ls = 0.75 H (Cc may be neglected). Table 1 shows a summary of the calculations required for this example.
Conclusions
The RIAA equalized noise of the ADC-27 phono cartridge and pre amp input network was 0.73 µV for the audio band. This is the limit for S/ N ratios if the preamp was noiseless, but zero noise amplifiers do not exist. If the preamp noise voltage was 0.64 µV, then the actual noise of the system is 0.97 µV (1(0.64)2 + (0.73)2 µV) or-66 dB S/N ratio (re: 2mV @ 1 kHz input). This is a 4 dB loss, and the preamp current noise will degrade this even more.
Thus, it is apparent that present phono preamp S/N ratio measurement methods are inadequate for defining actual system performance and that a new method should be used, one that reflects true performance instead of hollow specs.
References
1. Hallgren, B.I., "On the Noise Performance of a Magnetic Phonograph Pickup," J. Audio Eng. Soc., Vol. 23, pp. 546-552, (Sept. 1975).
2. Fristoe, H.T., "The Use of Q Equations to Solve Complex Electrical Networks," Engineering Research Bulletin, Oklahoma State University, 1964.
3. Korn, G.A. and T.M., "Basic Tables in Electrical Engineering," McGraw- Hill, New York, New York, 1965.
4. Maxwell, J., "The Low Noise JFET--The Noise Problem Solver," National Semiconductor AN151, (Sept. 1975).
(Audio magazine, March 1977; by John Maxwell [Senior Engineer, National Semiconductor, Santa Clara, Calif.] )
Also see:
A New Suspension System for Phono Styli (Mar. 1976)
= = = =