by NORMAN H. CROWHURST
IN A PREVIOUS ARTICLE, we developed a feedback oscillator with high stability and limited frequency range, the essential features of which are repeated at Fig. 1. Transistor Q1 is the high-gain stage utilized for oscillation, Q2 is a phase splitter, Q3 a saturating transistor that controls positive feedback, Q4 a d.c. amplifier controlling the saturating transistor, and Q5 an emitter follower to isolate the control-voltage rectifier from the main output.
This circuit gives a sinusoidal output signal of 4.5 volts peak to peak, using a supply of 16 volts. When I designed this circuit, I wanted a larger signal than this, without having to use a larger supply voltage, so the next problem was to amplify this to an adequate, stable magnitude, without distorting it.
One method is to use another phase splitter (Fig. 2) in which the emitter load produces a duplicate of the input 4.5 volts peak to peak, and the collector produces an enlarged version. If the collector resistor is double the emitter resistor, the signal voltage will be doubled, to 9 volts peak to peak.
As the signals at emitter and collector are in opposite phase, the two must be additive, in terms of the total load resistance, 180 + 360 in the values shown.
So the total swing is 4.5 + 9 = 13.5 volts peak to peak. This is cutting it fine, from a 16-volt supply, but with careful biasing of the transistor it may be possible.
If the transistor has a mean beta of 100, with limits 70 and 140, the emitter resistor will reflect at the base as a mean value of 18K, varying from 12.6K to 25.2K. To allow margin for this operation, the emitter needs to be biased to +3 volts (a little more than half 4.5 volts) and the lower resistor in the base can be 4.3K, to swamp the base input variations.
The average value from base to ground will be 18K in parallel with 4.3K, or 3.5K, varying from 3.2K to 3.67K. Using a 15K resistor from supply plus to base, will set the base voltage at an average of 3.5/18.5 times 16 volts, or 3 volts, the required value, with variation from 2.8 to 3.15 volts, which remains just about workable.
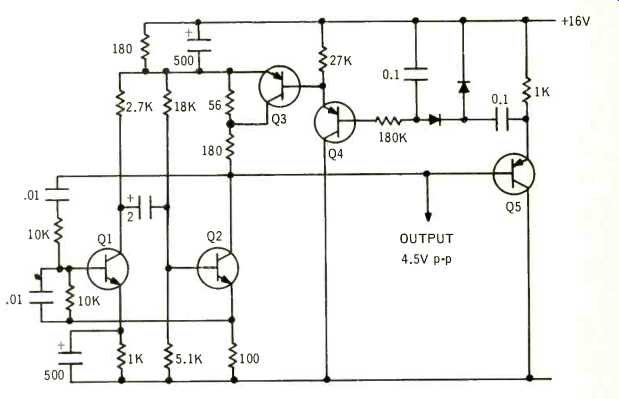
Fig. 1. The basic, stable oscillator, developed in the previous article,
that forms the starting point for this one.
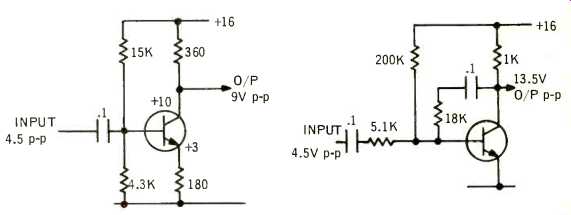
Fig. 2. A stage that gives a stable gain of 2:1, with well-stabilized operating
position. It is limited to an output less than two-thirds of supply voltage.
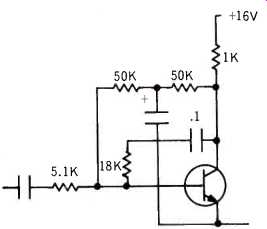
Fig. 3. A method of getting a bigger output swing, not much less than supply
voltage, peak to peak, but in this simple form, stability of operating point
is a problem.
The drop in the collector resistor will be double that in the emitter, an average of 6 volts, varying from 5.6 to 6.3 volts.
Extreme values of beta will cut the operational margin fine, to say the least.
A bigger output swing could be achieved, if the emitter did not subtract the input swing from it, which leads to the notion of eliminating the emitter resistor (Fig. 3 ). Here, the relative amplitude of output against input is obtained by negative current feedback from collector to base.
We have assumed the transistor has a beta of exactly 100. The 200K bias resistor will provide exactly 80 microamps base current, causing the d.c. collector current to be 8 milliamps and collector voltage 8 volts. Now, the 0.1 uF and 18K provides a.c. feedback. Here it is easiest to figure in peak volts: 13.5 volts peak to peak is 6.75 volts peak. The total collector load is 1K in parallel with 18K (assuming no other load for the moment) or 950 ohms.
A peak voltage of 6.75 across 950 ohms requires a signal current from the transistor's collector of 6.75/950 = 7.1 milli amps. This means, with a beta of precisely 100, that the base input signal must be 71 microamps. The signal current through the 18K feedback resistor will be 6.75/18K or 375 microamps. So the total signal input at the base needs to be 375 + 71 = 446 microamps.
The available signal voltage input is 4.5 volts peak to peak, or 2.25 volts peak.
This sets the input resistor at 2.25 volts/ 446 microamps or 5.05K, which is pretty close to a preferred value of 5.1K. This circuit will work fine, if the transistor's beta is precisely 100. From the a.c. point of view it is not too critical: the feedback factor is 446/71 = 6.3, or about 16 dB. But for the d.c. operating point, it is extremely critical. For betas of 70 and 140, the 80 microamps base current will yield collector currents of 5.6 and 11.2 milliamps, which will change the collector voltage from its nominal 8 volts, to 11.4 volts and 4.8 volts respectively. More than a volt deviation from the nominal 8-volt operating point is not permissible.
This could be improved a little, by using d.c. feedback from the collector to the base. Figure 4 shows one way, although the decoupling is not necessary, because the d.c. feedback being less than the a.c., it can be figured as part of it.
However, looking at it this way enables the two to be treated separately, and the a.c. feedback calculations for Fig. 3 can stand for this circuit.
The easiest way to figure this arrangement for d.c. is to regard the transistor as a resistor, controlled by its beta. If the beta is 100, its resistance is the d.c. feedback resistance of 100K divided by 100, or 1K, so collector voltage is half supply voltage, or 8 volts. If beta is 70, the transistor's d.c. resistance is 100K divided by 70, or 1.43K, and collector voltage rises to 9.4 volts. If beta is 140, the transistor's d.c. resistance is 100K divided by 140, or 175 ohms, and collector voltage drops to 6.7 volts. This is still an unacceptable deviation for this purpose.
Figure 5 shows a way of providing amplified d.c. feedback for such a stage. Q1 is the original amplifying stage, while Q2 and Q3 provide d.c. feedback. First the d.c. must be isolated from signal. As we plan to use an 18K resistor for a.c. feedback, reversing the positions of the 0.1-µF capacitor and this resistor allows the same pair of components to pick off a d.c. value, at the base of Q2.
Transistor Q2 acts as an emitter follower, direct coupled to the emitter of transistor Q3, whose collector current thus follows the emitter current of Q2.
Transistor Q3 has its base coupled to a mid-voltage reference point, which thus controls the emitter voltage of Q3. The only variation of the collector voltage of Q1 from the mid-voltage value is due to the drop in the 18K resistor, plus any variation due to the base current of Q3.
First assume Q1 and Q2 both have a beta of 70, combined gain 4900. For Q1 to have a collector current of 8 milliamps, its base current must be 114 microamps, and the base current of Q2 needs to be 1.6 microamps. The drop in 18K is about 30 millivolts. Now assume they both have a beta of 140. Q1 base current must be 57 microamps, and base current of Q2 must be about 0.4 micro-amp, so the drop in the 18K resistor is about 7.2 millivolts.
With the base current of Q1 thus controlled, the drop in the 10K resistor, due to base current from 57 to 114 microamps, varies from 0.57 to 1.17 volts, at the collector of Q3.
The extremes of current--at Q3 base are 0.4 and 1.6 microamps. With no current, the voltage is +8 (half supply) and the internal resistance as a voltage source is 500K. The drop in voltage will vary from 0.2 to 0.8 volts. This is the major cause of d.c. voltage variation. If it is too much, smaller resistors than 1 megs can be used.
For the a.c. feedback, the base of Q2 also shunts the feed through the 0.1-µF capacitor to the base of Q1. The resistance at the emitter of Q3 is 500K divided by the beta of Q3, which produces a minimum value of 3.6K. This reflects through the base of Q2, multiplied by the beta of Q2, which yields a minimum value of 250K. Obviously this is no serious shunt to the base input of Q1, and lower values than 1 meg could be used for the voltage divider.
The time constant formed by the 10-µF and the 10K-resistor is 0.1 second, which is the time it takes for the voltage at Q1 collector to adjust to its working value, giving a high stability. 'It is otherwise decoupled from the collector circuit by the collector impedance of Q3.
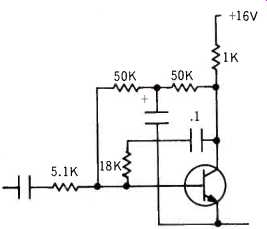
Fig. 4. Changing the circuit of Fig. 3 to provide d.c. feedback reducing
the operating point variation with transistor beta.
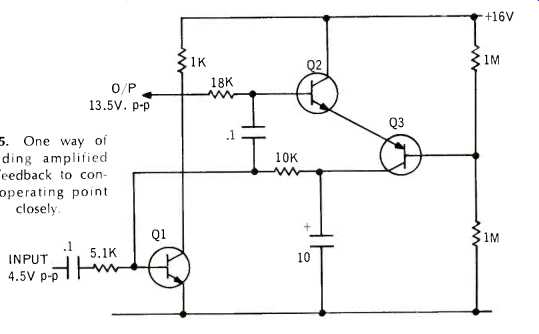
Fig. 5. One way of providing amplified d.c. feedback to control operating
point closely.
Another Approach
This is one of many design approaches to a sine-wave generator, based on the use of frequency discriminating networks and gain control, in this case in the components of the circuit of Fig. 1. Change of frequency necessitates change of the circuit values in the base circuit of Q1 in Fig. 1, where the values shown produce 1600 Hz.
And stability at its best is a sort of "bouncy" thing, because gain requires adjusting very critically, even though it is done automatically by d.c. feedback.
If the gain is a whisker too high, amplitude builds up, if it is a whisker too low, it dies away. Only when amplitude has adjusted itself right, do the gain and amplitude remain steady.
This problem is common to all oscillators of this type, because of the variables chosen as basis for the design: frequency and amplitude. Most modern generators employ a quite different basis, which can be made much more stable: time and amplitude, followed by wave shaping. This is known as a function generator.
A triangular waveform can be made by alternately charging and discharging a capacitor at a rate of constant current. The current is controlled precisely by circuit parameters. The points at which the direction of current flow is reversed are also precisely controlled, thus setting the amplitude of the triangular wave as a primary parameter. Finally, having a stable triangular wave, its shape can be changed precisely to sine-wave form.
This kind of circuit has no bounce and absolute stability of both period and amplitude. The older sine-wave oscillator used frequency networks (which originally were tuned circuits, but later were replaced by half bridges and other arrangements), to select the frequency of an essentially sinusoidal oscillation.
Deviation of parameters changed frequency rather than timing, and gain--that is, rate of growth or decay--rather than amplitude. The function generator reverses this procedure. The first thing set by the electronic circuitry is the timing and amplitude of the wave, which is then shaped as desired, where before the shape was first, and then frequency and amplitude were controlled to meet other requirements.
In the next article, we will show how a function-generator type of oscillator can be developed with solid-state circuit elements.
(adapted from Audio magazine, Jun. 1970)
Also see:
Negative Feedback by Norman H. Crowhurst (Apr. 1970)
Negative Feedback by Norman H. Crowhurst (May 1970)
More on Negative Feedback (Feb. 1970)
The Wonderful World Of Integrated Circuits (Jun. 1970)
= = = =