
By F. Alton Everest
The crowd noise was deafening.
In fact, how deafening was the subject being investigated. The occasion was the return of Col. Charles Lindbergh to New York after his historic solo flight across the Atlantic in 1927. New York City was in the process of giving this hero a ticker-tape welcome of a magnitude only New York could offer. As the aviator arrived at the southern tip of Manhattan, boat horns added to the din of the crowd.
Three-quarters of a mile up Broadway, at an open fifth-floor window, a very busy man seemed to be paying little attention to the excitement in the street below as he puttered with various pieces of equipment. Occasionally he leaned out the window to check the progress of the parade, only to lose himself once more in deep concentration over the equipment.
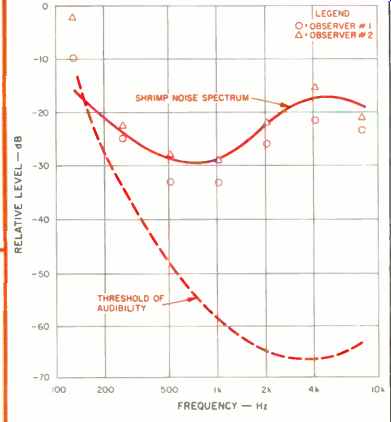
Fig. 1--Masking of pure tones by shrimp noise. The solid curve represents
the critical-band spectrum of shrimp noise recorded off Point Loma. The circle
and triangle points represent 50% recognition, by two observers, of pure
tones in the presence of shrimp noise. Note how closely the noise spectrum
can be approximated using only the auditory filters of the observers. An
arbitrary 0-dB reference point has been selected for convenience. (2)
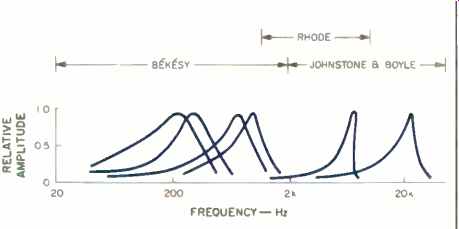
Fig. 2--A comparison of the shapes of "tuning curves" of the basilar
membrane obtained by three different sets of researchers. Each curve was
obtained by measuring the amplitude of vibration at a particular point on
the basilar membrane for a given frequency of stimulation. Békésy's early
measurements were made on dead animals at excessively high sound levels.
The sharper and more reliable curves of later investigators were taken on
live animals at modest sound levels. (10)
He was measuring the noise of the parade, using the filters in his head.
The telephone receiver he pressed to his ear carried a warble tone. An offset cap on the receiver let the crowd noise flow unimpeded into his ear, mixing acoustically with the warble tone from the diaphragm. A calibrated attenuator in the warble-tone circuit was adjusted until the tone was just masked by the noise. Comparison of this attenuator setting to a setting obtained previously under very quiet conditions gave a measure of what this investigator called the "deafening effect" of the noise. Today we would call this a "masking effect." Only those components of noise near a tone are effective in masking that tone, as will be more fully described later.
Lindbergh's triumphant procession along Broadway was certainly an historic event, but so was what was happening at that open fifth-floor window that day. The Bell Laboratory scientist, Rogers H. Galt, described his novel acoustical experiment in the first volume of the journal of the newly organized Acoustical Society of America[1]. Galt was measuring noise and recording noise audiograms of various stages of the parade. He found the "deafening effect" of the noise during a lull in the parade to be 40 dB in the region of 750 Hz to 1.5 kHz; this increased to 70 dB as Lindbergh passed close by. The sound of the boat horns almost a mile away was very intense at low frequencies, yielding a 55-dB "deafening effect" in the region of 250 to 750 Hz. As Galt adjusted the warble tone until it was just audible in the crowd noise, he was actually using his own aural critical band centered on the tone to measure the masking effect of the noise at the tone's frequency.
For me, this idea of auditory filters stirred up hazy memories of World War II, when I was engaged in undersea acoustical research under a University of California contract with the National Defense Research Committee at what is known today as the Naval Ocean Systems Center in San Diego. For assistance in recalling those evanescent memories, I sought out Robert S. Gales, an associate in my wartime work, past president of the Acoustical Society of America and now a consultant in acoustics in San Diego. He replied by sending a copy of a report, "The Effect of Shrimp Noise on Audibility of Underwater Sounds" [2], a product of his psycho-acoustical laboratory efforts during the war. The "Confidential" stamps on the report had "Void" stamped over them as evidence of declassification. The reason for my hazy memories was then disclosed, as I saw my own name on the distribution list! What could a tiny shrimp do that might affect the course of a world war? Studies of underwater sounds in the sea off Point Loma had disclosed areas dominated by intense crackling and sizzling sounds associated with rocky sea bottoms. Scientists at the Scripps Institution of Oceanography found that populations of millions of inch-long shrimp make this noise by repeatedly snapping their tiny claws together [3, 4].
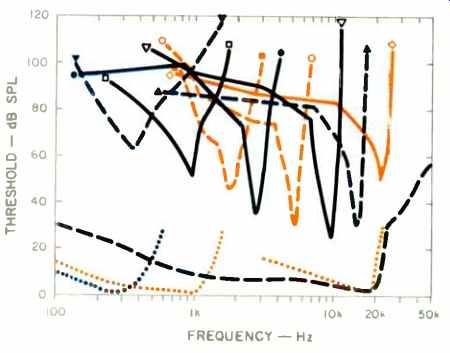
Fig. 3--A sample of threshold tuning curves of single nerve fibers in the
auditory nerves of an anesthetized cat. For each fiber, the threshold is
plotted as a function of the stimulating frequency. The dotted and dashed
curves at the bottom show corresponding measurements from the basilar membrane.
The sound level required to produce a constant amplitude of vibration at
a particular point on the basilar membrane is plotted as a function of frequency.
The position of these curves on the ordinate is arbitrary; they hove been
shifted downward for clarity. (9; reprinted by permission of Grune & Stratton,
Inc. and the author.)
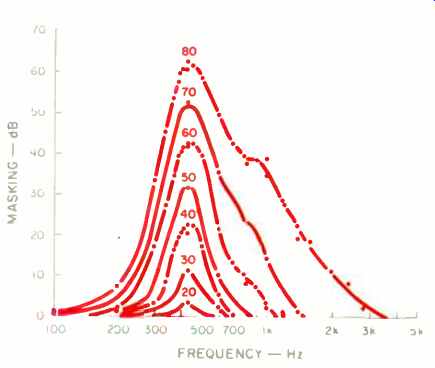
Fig. 4--Masked audiograms for a 90-Hz band of noise centered on 410 Hz.
Each curve shows the elevation of pure-tone threshold is a function of frequency
for a particular level of the masking noise. (18; reprinted by permission
of the authors and JASA.)
The U.S. Navy became very interested in the effects of such noise on detectability of ship and submarine sounds and echo-ranging systems.
This is where Bob Gales' listening experiments came in. In a typical test, he presented to the listener, through headphones, typical shrimp noise at a constant, comfortable level of 60 phons. The level of a tone of a given frequency was then adjusted by a calibrated attenuator until it was just masked by the shrimp noise. This was repeated at different frequencies and with different listeners. The circles and triangles of Fig. 1 show the results of one such test. The solid line of Fig. 1 is an analysis of the shrimp noise used in the test, made with an analyzer having a 50-Hz bandwidth. The 50-Hz values were then corrected to commonly accepted critical-bandwidth values to make them comparable to the psycho acoustical results of the experiment. It is seen that there is quite close agreement between the analysis made by the auditory filters of the two observers (circles and triangles) and the spectral analysis made by the 50-Hz filter adjusted for critical bandwidths. Taking into account the inevitable variation in critical bandwidths from one observer to another, as well as the usual variables of subjective measurements, the agreement between the two systems of spectral analysis is surprisingly good-except at 125 Hz, where poor ear sensitivity was the limiting factor.
This demonstrates that the spectral shape of a noise may be at least roughly estimated with no other filters than those in the observers' heads.
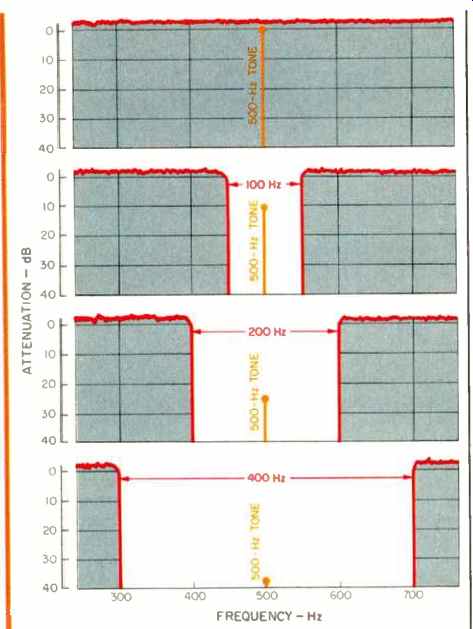
Fig. 5--The "notched-noise" method of determining the bandwidth
of auditory filters. The tone, which is represented by the line of 500 Hz,
is taken to be just audible at the levels shown. These values ore plotted
in Fig. 6.
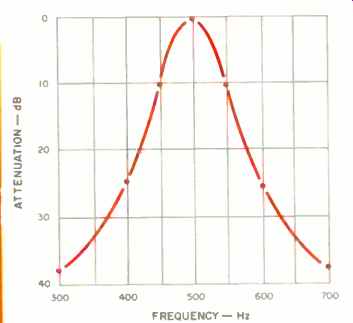
Fig. 6--Auditory filter shape derived from the notched-noise method illustrated
in Fig. 5. This method minimizes the effect of adjacent critical bands and
assumes a symmetrical shape.
The Concept of Critical Bands
Anatomical and physiological methods dominated the search for the secret of the ear's analyzing ability for almost a century before the introduction of psycho-acoustical methods. In 1924, Wegel and Lane [5] reported on the masking of a tone fixed in frequency and amplitude by a second tone of adjustable frequency. When the two tones were close together, "beats" occurred which distorted the results.
To avoid such beats, Fletcher in 1940 [6] used white noise, which has energy uniformly distributed throughout the audible spectrum. He measured the ratio between the level of the white noise and the level of a tone just audible in that noise, and he found this ratio to vary with tones of different frequencies. Fletcher made two assumptions which had far-reaching consequences: First, that only a narrow band of noise surrounding the tone contributes to the masking of the tone, and second, that when the noise just masks the tone, the power of the noise in this band (the critical band) is equal to the power in the tone.
The first assumption proposes the critical band concept, and the second opens up the possibility of estimating the width of the critical bands. Noise power is expressed in terms of the power in a band 1 Hz wide; this is called the spectrum level. If a distributed noise measured with an analyzer having a 50-Hz bandwidth gives a sound pressure level of 60 dB, the spectrum level of the noise at that frequency is: 60 10 log 50 = 43 dB. The overall level of a pure tone is identical to that in a 1-Hz band, as the width of the tone is very narrow compared to 1 Hz. Fletcher easily obtained the spectrum level of the white noise by simple measurement. The ratio of the spectrum levels of the tone and the white noise then yielded a bandwidth, which Fletcher called the critical band, that was effective in masking the tone.
The bandwidths so determined, as time went on, were found to be about 2.5 times narrower than those determined by more direct methods. Researchers labeled Fletcher's bands "critical ratios" to preserve the integrity of the more basic term "critical band." In Fletcher's second assumption, the signal-to-noise ratio in the critical band of a tone at threshold in white noise is 0 dB. If this is changed to -4 dB (10 log 2.5), critical ratios become equal to critical bands. The genius of Fletcher's work is that it gave new understanding of, and appreciation for, the "filters" of the auditory system.
An avalanche of psycho-acoustical studies of critical bands followed Fletcher's 1940 report. There was a continuation of work on the masking of one tone by another tone, but this approach was plagued by the distortion of results by beats created when the frequency of the masking tone approached that of the masked tone. This problem was eliminated by employing a narrow band of noise with an exploratory tone. Various combinations of paired tones were also used by some experimenters, while others used "notched noise," which will be considered later.
At this stage, one might be tempted to jump to the conclusion that the critical bands of the human auditory system are similar to the set of filters in a real-time analyzer. Although critical bands are somewhat comparable in width to 1/3-octave filters, the similarity ends there. The ear's critical bands are continuous, in that a tone of any audible frequency presented will find a critical band centered on it. It is not a matter of adjacent bands overlapping at the -3 dB points, as is common in filter sets, requiring about 30 filters to cover the audible range. Our ears have literally thousands of critical-band filters standing ready to respond to test tones or to fundamentals, harmonics, and partials of complex signals.
Frequency Selectivity
Nobel prizes are given only to those who have made outstanding contributions in their fields. One such prize was given to Georg von Békésy, a Hungarian scientist, for his work on the hearing mechanism. One of his numerous experiments involved standing waves in the ears of animals. Using a microscope and stroboscopic illumination, he measured the amplitude of these waves on the basilar membrane of each animal's cochlea as its ear was stimulated by tones of various frequencies. He measured the envelopes of vibration patterns, which showed peaks distributed along the basilar membrane according to the frequency of the tone falling on the ear. High frequencies created peaks toward the oval window (to which the stapes is attached), and low frequencies created peaks toward the opposite end, the apex of the cochlea. Békésy demonstrated that the cochlea was a sort of Fourier analyzer.
Tuning curves derived in this manner gave rise to the so-called "place theory," which states that the frequency selectivity of the ear results from the mechanical vibrating system associated with the basilar membrane. Different frequency components of an impinging sound, thus sorted out, were thought by some to be the final answer to the analyzing ability of the ear. The tuning curves obtained by Békésy are illustrated at the left in Fig. 2.
In science, wrong answers are sometimes as valuable as right answers, as they raise new questions and stimulate the formation of new models.
Békésy's experiments served to focus the attention of many researchers on the problem. However, the tuning curves he obtained were too broad to explain ear selectivity as revealed by other experiments.
The techniques of Békésy were refined by others. Stroboscopic illumination was replaced by an approach employing the Móssbauer effect, in which a tiny speck of material emitting gamma rays was fixed to the basilar membrane. Changes in the velocity of the gamma rays, produced by motion of the membrane, could be detected by a Doppler shift method. This yielded a tremendous increase in test sensitivity.
Békésy was forced to use sound levels of 140 dB to get measurable basilar membrane amplitudes, but with the Móssbauer principle, sound levels of 70 to 80 dB could be used. As shown in Fig. 2, such experimenters as Johnstone and Boyle [7] and Rhode [8], using the new method on live animals, found much sharper tuning curves than Békésy found with dead animals.
This sharpening of the tuning curves is attributed to the use of normal sound levels and the presence of metabolic processes [ 10]. The slopes of Békésy's tuning curves range from about 6 dB/octave on the low-frequency side to 20 dB/octave on the high-frequency side. The corresponding slopes reported by Johnstone and Boyle for live animals [7] are 13 and 105 dB/octave.
Such measurements made on the cochlea of small animals cannot be equated to those made on humans, but in general the auditory systems of all mammals are strikingly similar.
A Second Filter
The improvement in observed frequency selectivity, while interesting, was still not enough to soften the cry for the existence of a "second" filter; the far greater selectivity revealed by other types of experiments required more than basilar-membrane activity.
For example, humans are able to distinguish between tones of 1,000 and 1,004 Hz, a difference of only 0.4%. It was recognized that basilar-membrane action excites the hair cells which are connected to the auditory nerve bundle. It was reasoned that any further filtering action following the mechanical filtering of the basilar membrane would have to be found in the hair cells associated with the membrane, in the nerve fibers making up the auditory nerve bundle, or in the auditory cortex of the brain.
By inserting a microelectrode in an individual fiber of the auditory nerve and noting the pattern of neuron firings as the ear is stimulated by tones of varying frequency, beautiful tuning curves were obtained. Figure 3 shows such tuning curves of single nerve fibers in the auditory nerves of an anesthetized cat [9]. The sharpness of nerve-fiber response is in stark contrast to the basilar-membrane response shown in the lower part of the figure. (The basilar-membrane responses of Fig. 2 are vibration amplitudes measured along the membrane when it is excited by sound of different fixed frequencies. Those in the lower part of Fig. 3 show the sound level required to produce constant amplitude of vibration at a particular point on the membrane, as a function of frequency.) The tuning curves of individual auditory nerve fibers are obtained by counting nerve impulses. The fibers show a certain spontaneous firing rate with no sound stimulation; each fiber shows frequency selectivity of the type shown in Fig. 3 by an increase in firings above the spontaneous firing rate.
Fibers also show phase-locking to a tonal stimulation: A given neuron does not always fire on every cycle of the stimulating tone, but when it does, it fires at the same phase of the stimulating waveform. Above about 5 kHz, such phase-locking is replaced by a "jitter" which smears the firings over each cycle. An interesting observation is that the nerve fibers' characteristic frequencies (frequencies of peak response, as in Fig. 3) are distributed throughout the auditory nerve bundle in an orderly manner. Fibers responding to higher frequencies are found nearer the surface, and lower frequency fibers nearer the center of the nerve bundle.
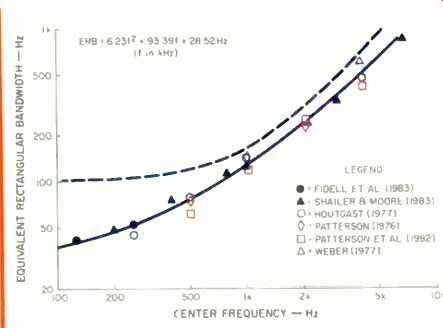
Fig. 7--The symbols indicate measurements of the equivalent rectangular
bandwidth (ERB) of the auditory filter at various center frequencies, token
from the results of the researchers indicated. The curve fitted to the data
is specified by the equation in the figure. The dashed curve is the classical
critical band function. (14)
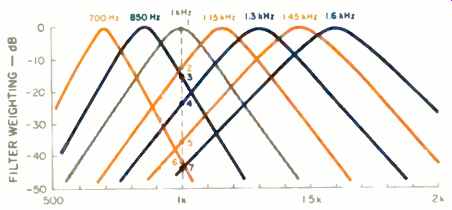
Fig. 8--Simplified filter shapes at several center frequencies. These are
calculated according to Moore and Glasberg's equation, with the filter shapes
assumed to be symmetrical.
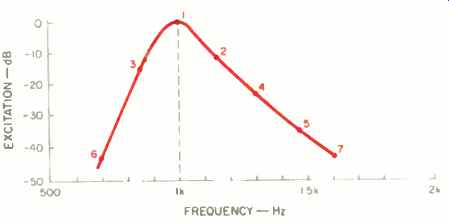
Fig. 9--The excitation pattern for a 1-kHz tone, derived from the filter
shape in Fig. 8. The pattern is obtained not only from the 1-kHz auditory
filter but also from the contributions of the adjacent filters' skirts. (14)
Each nerve fiber has a certain "dynamic range," limited by a "noise level" (spontaneous firings without excitation) at lower levels and by a saturated region at higher levels. As this range is only about 20 to 50 dB, we must look elsewhere to explain the much greater overall dynamic range our ears exhibit.
Measuring neuron firings has been a most productive approach, but it tells us nothing about the pattern of distribution of firings over different neurons, an important Pandora's box yet to be opened.
The Shape of Critical Bands
For measuring convenience, Fletcher assumed that critical bands were rectangular in shape, but he did not really think they were. Schafer and Gales, in their masking experiments reported in 1950, had reasonable success in fitting simple resonance curves to their critical-band data. It is very interesting that they used the universal resonance curves straight out of Terman's book Radio Engineering [11]. Convinced that some sort of rounded top to the tuning curve would be eventually vindicated, other experimenters tried fitting the Gaussian bell-shaped curve to their data. The masked audio grams of Fig. 4, also reported in 1950, show rounded tops, although allowance must be made for the 90-Hz band of noise involved in their determination.
A distinctive feature of the masked audiograms of Fig. 4 is that the slopes are steeper on the low-frequency side of the peak than on the high-frequency side. This is especially pronounced at the higher sound levels, which suggests that at higher levels, responses of adjacent critical bands come into play. How can the shape of an individual critical band be examined without adjacent, overlapping critical bands affecting the result? One way is to make observations at low levels, closer to threshold. Those audiograms of Fig. 4 taken at low levels are more symmetrical than those at higher levels, but detail is limited.
Patterson, in 1976, used a "notched noise" method of obtaining masked audiograms [12]. Figure 5 illustrates the general principle involved, although not necessarily the mechanics.
First, the threshold of audibility of a 500-Hz tone in wide-band noise is determined. Let us say that this tone level is 0 dB. A notch is then cut into the white noise with filters having very sharp boundaries at 450 and 550 Hz.
The tone level is again adjusted until it is just extinguished and is found to be at a level of-10 dB. The notch is widened to 400 and 600 Hz, and the tonal threshold is found to be-25 dB. Widening the notch in the white noise to a total width of 400 Hz further reduces the masking effect, to-38 dB. These masking values are plotted in Fig. 6; of necessity, a perfectly symmetrical critical-band shape emerges.
What has been accomplished is that the subject being tested is forced to attend to a single critical band rather than listen for the best S/N ratio.
Using the notched-noise or other similar method, remarkably consistent results have been obtained by numerous researchers, as shown in Fig. 7. In this figure, the "equivalent rectangular bandwidth" of the human auditory filter is plotted against frequency. The solid curve, computed from the equation indicated, fits the experimental points closely. The dashed-line curve is the classical critical-band function. The most striking revelation is that critical bandwidth derived this new way continues to decrease below 500 Hz.
Once symmetry is attributed to individual auditory filters, the next logical step is to calculate their shapes. Moore and Glasberg [14] have derived such an equation which fits experimental data well within 25 to 30 dB of the peak (which, after all, is the most important part). A series of such auditory filter shapes is shown in Fig. 8. It is now possible to explore the effect of adjacent filters. In Fig. 9, an "excitation pattern" (as contrasted to a filter shape) at 1 kHz is built up by including the contributions of adjacent filters.
The filter centered on 1 kHz contributes the response indicated by point 1, but the other filters shown in Fig. 8 contribute, too: The filter centered on 1.15 kHz contributes response point 2, the one centered on 850 Hz contributes point 3, and so on. By plotting each response contribution at the peak frequency of the filter giving rise to the response, as is done in Fig. 9, the shape of the excitation pattern is revealed. This shows how continuous symmetrical auditory filters can yield a masked audiogram that is asymmetrical, even on a linear frequency scale.
There is some slight feeling that critical-band auditory filters might not actually exist. Some researchers believe that when more is known of neural activity in the inner ear, the auditory nerve, and the auditory cortex, the filtering effect may possibly be explained in another way. However, there is no uncertainty that some sort of filtering agent is very active in most of our hearing functions. This being the case, one might wonder what sort of practical effect such auditory filters exert.
Ear Damage
Much has been written about nerve damage to the inner ear resulting from mixing sound at excessively high levels, listening to reproduced music at high levels with headphones or loudspeakers, or even working around noisy machinery. Loss of high-frequency sensitivity due to such exposure has been well documented. Another consequence of nerve damage to the inner ear is that the auditory filters become broader and less selective [13]. Such broadened filters result in deterioration of every type of listening activity in which critical bands play a part.
For example, when we try to detect a desired sound in the presence of noise, we unconsciously attend to the auditory filter which gives the best signal-to-noise ratio. The increased width of that particular filter in the impaired ear would pass more noise and yield a poorer signal-to-noise ratio. The broader critical bands of the impaired ear result in difficulty of hearing in noisy environments, picking out one voice in the presence of other voices, and evaluating differences in the timbre of music and the spectral composition of sounds.
Timbre, Consonance, and Dissonance
Timbre involves the perception of the quality of a complex sound. This, of course, is related to its spectrum, including its fundamentals, harmonics, and partials. The spectrum is measurable with sound analyzers, but timbre is strictly a subjective phenomenon, requiring psycho-acoustical measuring procedures.
Tones that are separated by an octave (a 2:1 frequency ratio) have a certain essential similarity which sounds pleasant to our ears. The musical fifth has a 3:2 ratio, the major third a 5:4 ratio, and the minor third a 6:5 ratio.
Musical notes played in these ratios are also pleasant to our ears; we call them consonant (although trained musicians are inclined to distinguish between the terms pleasant and consonant). Certain modern composers have deviated slightly from these ratios, resulting in music that is dissonant, but enjoyed by many.
Critical bands play an important role in determining whether certain combinations are consonant or dissonant.
Simple tonal intervals are evaluated as consonant if their frequency difference is greater than a critical band. If two tones fall within a critical band, beats occur; if the beat frequency exceeds about 20 Hz, a sensation of roughness sets in which persists up to a beat frequency of 150 to 200 Hz. This roughness is sensed as dissonance.
Figure 10 summarizes the results of many listening tests [15]. The most dissonant intervals are those associated with frequency differences of about one-fourth of a critical band.
The degree of consonance or dissonance is nearly uniform over a wide frequency range, as shown in Fig. 11.
The curves for the different ratios each tend to fall below some critical frequency, where they tend to become more and more dissonant. This is due to the bend in the critical-band curve below 500 Hz (see Fig. 7). The increase in dissonance at lower frequencies explains the musical practice of avoiding thirds at low frequencies and using octaves or greater intervals.
The curve for the octave relationship (1:2 ratio) of Fig. 11 shows a dissonance of zero up to the sixth harmonic, and all spacings between these harmonics are greater than the applicable critical band. This explains why complex tones with strong higher harmonics sound sharper than tones having only six harmonics. Curiously, we are catching up with von Helmholtz, who pointed out this fact 100 years ago!
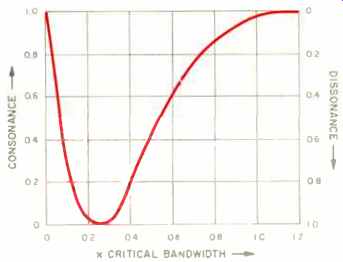
Fig. 10--The pleasantness (consonance) of two simple tones with varying
frequency difference, expressed in terms of fraction of a critical band.
The curve is obtained from many specific experimental studies. The consonance
and dissonance scales are arbitrary. (15)
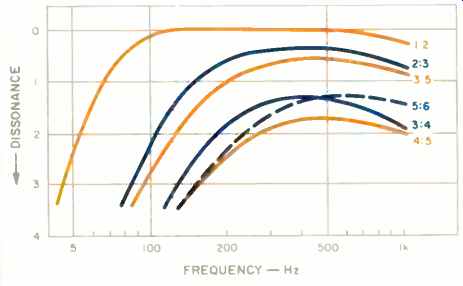
Fig. 11--Illustration of the way in which consonance of some intervals with
simple frequency ratios depends on the frequency of the lower tone. Both
complex tones used have six harmonics. (15)
Masking
There is a great debate among experimental psychologists as to whether masking results from a "swamping" of the neural activity of the signal, the suppression of neural activity by the masker, or a combination of the two. In fact, not too much is known about the coding of nerve impulses which describes the signal. It seems to be more than just a matter of how many neural discharges take place; it is strongly suspected that there exists some time pattern of discharges.
First off, masking is more a critical band channel effect than a simple level effect. Only the noise energy in the critical band surrounding a tone contributes to the masking of that tone. As we've seen, the shapes of the masked audiograms of Fig. 4 reveal that the slopes on the low-frequency side, ranging from 80 to 240 dB/octave, are much steeper than those on the high frequency side. If the level of a low frequency masker is increased by a given amount, say 10 dB, the masking threshold of a high-frequency signal would be raised considerably more than 10 dB. One can, therefore, generalize that in any speech or music signal, low frequencies mask high frequencies, but not the reverse. This "upward spread" of masking tends to reduce the perception of higher frequency signals that are so important in the intelligibility of speech and the brightness of music. Also, the masking effect is greater at higher signal levels, which explains why, in sound-reinforcement systems, very high levels of reproduction tend to reduce the intelligibility of speech.
Loudness
The loudness of a sound is determined by the summation of the sound energy over the critical bands involved. This may be illustrated by the age-old observation that commercials on radio and television often seem much louder than the program material. Presumably, someone (or some automatic equipment) up the chain is riding gain and holding it in line with a VU meter as reference. In spite of this, complaints pour in that the commercials are the loudest thing on the air.
There is a great chasm that exists between VU meter readings and loudness summation of the human hearing mechanism.
To bridge this chasm, loudness-level meters have been developed. Early work in this field was done by the late Ben Bauer and his colleagues at the CBS Technology Center [16, 17]. The ideal loudness meter might use 30 adjacent critical-band filters, but practical loudness meters utilize only eight. The outputs of the eight filters are linearly rectified and given a 10-mS attack and 200-mS decay characteristic to follow the time constants of the ear. These are then integrated and fed to an LED indicator. Basically, the signals in individual channels have been changed to loudness level (in phons) and then to channel loudness (in sones). The sones of each channel are then added to give an indication of overall loudness. Verification tests have indicated that loudness readings by this meter fall within 1 or 2 dB when commercials, music and songs, and male and female speech are compared to a standard noise. Note that the design of this loudness meter starts with critical bands.
Sometimes it is necessary to derive loudness from a series of sound-level meter readings in industrial situations.
Several tedious programs have been devised to do this, and they are all based on the critical band. Sound-level meter readings alone are not of much help because they yield physical, not psychophysical, data. However, wide-band, A-weighted sound level meter readings of two noises can give a rough approximation of relative loudness. For a rough-and-ready evaluation of the relative loudness of two sounds, comparing dBA readings is the way to go.
Have you ever wondered why a seriously distorted signal sounds louder than the same signal in undistorted form? This phenomenon is rather simple to understand when auditory filters are taken into consideration. The distortion products (harmonics) fall in other critical bands than that of the fundamental, hence their power adds to that of the fundamental.
Phase
The famous AM/FM experiment is often cited as evidence that the human hearing system is somewhat sensitive to phase. If an audible carrier tone is amplitude-modulated by another tone, three frequencies result-the carrier, and upper and lower sidebands. The same is true in frequency modulation, except that there is a difference in the relative phase of the components. If identical frequencies are used, the two types of modulated waves should sound the same if the ear takes no note of the phase difference. If all three components fall within a single critical band, AM is more easily detected than FM; if they don't, FM and AM sound the same. Other experiments throw some questions on this conclusion, and further work is needed.
REFERENCES
1. Galt, Rogers H., "Methods and Apparatus for Measuring the Noise Audiogram," Journal of the Acoustical Society of America (JASA), Vol. 1 (October 1929), pgs. 147157.
2. Gales, R. S., "The Effect of Shrimp Noise on Audibility of Underwater Sounds," University of California Division of War Research, Internal Report No. A46, November 9, 1944.
3. Everest, F. Alton, Robert W. Young, and Martin W. Johnson, "Acoustical Characteristics of Noise Produced by Snapping Shrimp," JASA, Vol. 20 (March 1948), pgs. 137-142.
4. Johnson, Martin W., F. Alton Everest, and Robert W. Young, "The Role of Snapping Shrimp (Crangon and Synalpheus) in the Production of Underwater Noise in the Sea," Biological Bulletin, Vol. 93, No. 2 (October 1947), pgs. 122-138.
5. Wegel, F. L. and C. E. Lane, "The Auditory Masking of One Sound by Another and Its Probable Relation to the Dynamics of the Inner Ear," Physical Review, Vol. 23 (1924), pgs. 266-285.
6. Fletcher, H., "Auditory Patterns," Review of Modern Physics, Vol. 12 (1940), pgs. 47-65.
7. Johnstone, B. M. and A. J. F. Boyle, "Basilar Membrane Vibration Examined with the Móssbauer Technique," Science, Vol. 158 (1967), pgs. 389-390.
8. Rhode, W. S., "Observations on the Vibration of the Basilar Membrane in Squirrel Monkeys Using the Móssbauer Technique," JASA, Vol. 49 (1971), pgs. 1218-1231.
9. Evans, E. F., "The Sharpening of Cochlear Frequency Selectivity in the Normal and Abnormal Cochlea," Audiology, Vol. 14 (1975), pgs. 419-442. (Figure 3 in accompanying article reprinted by permission of Grune & Stratton, Inc. and the author.)
10. Johnstone, B. M. and P. M. Sellick, "The Peripheral Auditory Apparatus," Quarterly Review of Biophysics, Vol. 5 (1972), pgs. 1-57.
11. Terman, F. E., Radio Engineering, McGraw-Hill, New York, 1937.
12. Patterson, Roy D., "Auditory Filter Shapes Derived with Noise Stimuli," JASA, Vol. 59, No. 3 (1976), pgs. 640-654.
13. Zwicker, E. and K. Schorn, "Psycho acoustical Tuning Curves in Audiology," Audiology, Vol. 17 (1978), pgs. 120-140.
14. Moore, Brian C. J. and Brian R. Glasberg, "Suggested Formulae for Calculating Auditory Filter Bandwidth and Excitation Patterns." JASA, Vol. 74, No. 3 (September 1983), pgs. 750-753.
15. Plomp, R. and W. J. M. Levelt, "Tonal Consonance and Critical Bandwidth," JASA, Vol. 38 (1965), pgs. 548-560.
16. Bauer, B. B., E. L. Torick, A. J. Rosen heck, and R. G. Allen, "A Loudness Level Monitor for Broadcasting," IEEE Transactions on Audio and Electroacoustics, Vol. AU-15 (1967), pg. 177.
17. Jones, B. L. and E. L. Torick, "A New Loudness Indicator for Use in Broadcasting," SMPTE Journal, Vol. 90, No. 9 (1981), pgs. 772-777.
18. Egan, J. P. and H. W. Hake, "On the Masking Pattern of a Simple Auditory Stimulus " JASA, Vol. 22 (1950), pgs. 662-630.
(Source: Audio magazine, Sept. 1986)
Also see: Illusions for Stereo Headphones (Mar. 1987)
Noteworthy: How PASC Data Compression Works In Philips Digital Compact Cassette (Sept. 1991)
= = = =