
By now you must have heard about Philips' Digital Compact Cassette (DCC) system, a system whose decks will also be able to play analog cassettes. DCC is the first proposed digital audio medium that is playback compatible with the technology it is meant to replace. Tandy (Radio Shack and Memtek) is also a prime exponent of DCC and has supported the format in tandem with Philips since the initial announcement Although DCC tapes will play only on 'DCC machines, you’ll be able to play your old analog tapes on a DCC machine as well. The DCC system has other innovations and features (see the first side-bar), but this article will concentrate on only one of them. For many audiophiles; the most controversial aspect of the DCC system will be Precision Adaptive Sub-Band Coding (PASC); the data-reduction scheme that enables this degree of old/new compatibility.

DCC marks the first time that an audio product has employed the power of digital signal processing to create an electronic model of certain properties of human hearing. The PASC system inside a DCC recorder uses this model to calculate how much digital audio data is redundant or irrelevant to our perception of music information found to be unnecessary is then removed(!) from the data stream, and the "compressed" data is recorded using stationary heads or a tape running at the analog cassette speed of 1 7/8 ips.
Those who still think the CD doesn't carry enough audio information will be scandalized to learn that DCC carries even less, about one-quarter as much. Yet Philips makes the claim that DCC has CD-equivalent sound quality on music, and that their golden-eared listening panel can't detect the difference between music from a CD and a DCC-encoded recording of it.
Getting the Gist
Since Philips' January announcement of DCC, the company has been reluctant to release details about the system's principles of operation. If DCC follows the path taken by the Compact Disc, a great deal of information may remain trade secrets, at least until DCC is proposed as an official worldwide IEC standard. The lack of hard facts is why most previous articles you will have seen on DCC, including mine, have beer glosses on the initial Philips press kit.
But DCC didn't spring fully formed from the heads at Eindhoven. For PASC especially, there are other sources of highly relevant information. It turns out that important parts of the PASC process are identical or very similar to the corresponding portions of the MUSICAM data-reduction system being proposed for digital radio broadcasting both here and in Europe. (MUSICAM is an obviously forced acronym standing for (Masking pattern Universal Sub-band Integrated Coding And Multiplexing.) Philips is one of the co-developers of MUSICAM and one Philips engineer told me that a PASC chip-could also decode certain MUSICAM signals, a fact that carries many important implications about the way PASC operates.
Various non-Philips sources have been kind enough to provide me with some devils of MUSICAM operation, and it is on these details that much of this article is based. It covers only the fundamental principles applicable to both MUSICAM and PASC and, to some extent, other psychoacoustically based data-reduction schemes. When it comes to those areas where PASC and MUSICAM differ, there may be errors here in the details, especially in the graphs, charts, and any numerical specifications, so you won't be able to use this article to design your own homemade PASC decoder. (I've already tried, and it's very difficult.)
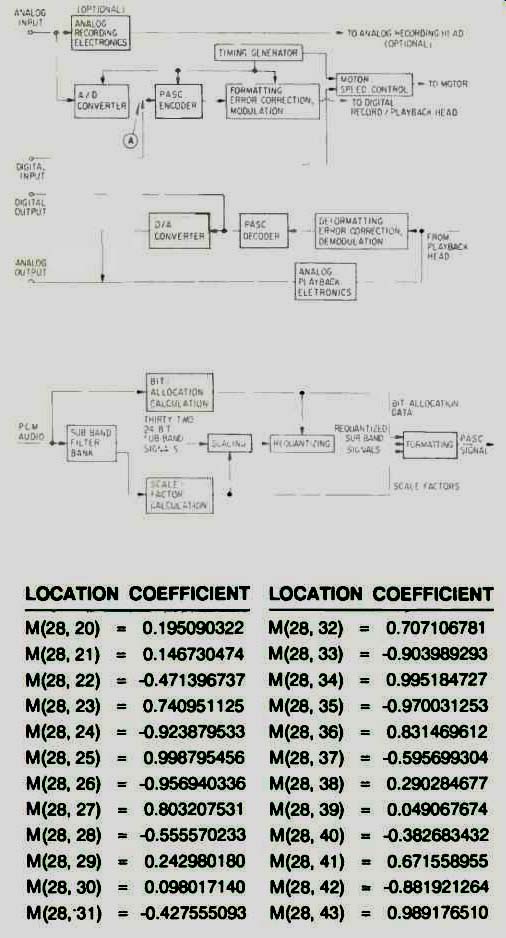
Fig. 1--Block diagram of a DCC deck.
Fig. 2--Block diagram of a PASC encoder.
Fig. 3--A short excerpt from the PASC digital encode/decode filter bank's coefficient table.
=========
DCC: A Compressed Review
Digital Compact Cassette is a digital audio recording .system utilizing a tape housing that deliberately almost identical to that of a conventional analog cassette. The main differences are the inclusion of a sliding protective tape cover, like that found on mini-floppy discs, and DCC's use of videotape-quality chromium-dioxide magnetic particles. There are still two g playable sides, to a DCC cassette, but the tape cannot be flipped lover. Instead, DCC machines will have some farm of auto-reverse system.
The tap speed, width, and playing times per side of DCC tapes are identical to the analog cassettes'. In addition to making digital recordings, DCC decks will also play analog cassettes. To make this possible; DCC machines will contain a head capable of analog playback (but not analog recording) as well as digital playback and digital recording, where applicable. The combination analog/digital head is made with thin-film techniques similar to those applied to making integrated circuits. Thin-film heads are already-used extensively in computer disk drives. Analog recording on a PASC deck requires the addition of a conventional analog, record-head.
The analog playback portion of a DCC head has the standard two audio tracks but the digital record/playback portion has eight tracks spaced 195 micrometers apart, each track being 185 micrometers wide. These tracks carry two channels of specially encoded digital audio data. A ninth-digital track carries auxiliary information for rapid machine-controlled cueing and other advanced features, The DCC digital error-correction system is said to a tolerate the loss of an entire digital track with no audible side effects.
DCC has three sampling rates, 32 1 kHz 44.1 kHz, and 48 kHz, which are used according to the digital / signal source (respectively: European digital radio, CD players, and analog inputs or a DAT machine). Philips explicitly intends DCC to ultimately replace the analog cassette and hopes that such versatility, combined with DCC's analog cassette playback capability, will make the transition easier.
=========
Inside a DCC deck
To another audio component, a DCC deck will look like just another cassette deck or DAT machine. It will have standard analog and digital inputs and outputs. But to get to the PASC data reduction encoder embedded within a DCC deck, the audio signal must be in standard digital form (linear pulse code modulation, or PCM). Analog signals fed to the inputs of a DCC deck are therefore digitized by standard analog-to-digital converters, just as in a DAT machine. I have been told that Philips' first PASC chips will accept data quantized with up to 18 bits of resolution, although the individual DCC licensee must decide whether to use cheaper 16-bit A/D converters on the analog inputs or deluxe 18-bit units with their potential dynamic range of greater than 100 dB.
With audio data now safely in the digital domain, we are at Point A of Fig. 1, which shows a conceptual block diagram of the primary subsections of a DCC recorder. It's what happens in the next block, the PASC encoder, that sets DCC apart from all other digital recording systems.
Band Splitting
In the first step of PASC encoding, the full audio signal is split into 32 sub-band signals, each sub-band spanning 1/32nd of the audio spectrum, by a bank of special digital filters (Fig. 2). The most important property of the PASC filter bank can be gleaned from the technical phrase used to describe the technique: Perfect reconstruction.
Using perfect-reconstruction filter banks, the frequency splitting of an encoding bank is completely and exactly reversed by the band-combining decoding bank. If no other processing were applied in between the encoding and decoding filter banks, the sequence of digital-audio samples coming out would be nearly identical to what went in--no phase shifts, no added distortions, no frequency-response changes, only a slight time delay, and possibly, depending on the precision of the calculations, a smidgen of added noise.
Perfect-reconstruction filter banks are feasible only with digital signal processing. Any attempt to use analog techniques would immediately be thwarted by unmatched and drifting component values, not to mention horrendous circuit complexity. A digital filter uses computer arithmetic in which operations can be precisely reversed or cancelled. Indeed, in a PASC chip, the same circuitry can be used for both the encoding and decoding filter banks.
For the math to come out right, the same table of numerical filter coefficients must be used in encoding and decoding. A small sample of such numbers is shown in Fig. 3. There are 2,048 of them in this portion of the PASC filter-bank process, and they are used in the repetitive multiplications and additions that make up the filter bank. The number of decimal places in these coefficients illustrates the precision to which the mathematical operations must be executed at these crucial stages to preserve sound quality. The numbers in Fig. 3 are decimal equivalents of 24-bit binary numbers. Calculations in the PASC filter bank are performed with 24-bit precision, which means that the mathematical results have a potential dynamic range (the span between the largest and smallest representable numbers) of about 146 dB. In practice, the dynamic range will probably be limited by the music signal. (In what follows, it is convenient to think of "precision" as the number of decimal places or binary bits used to portray a number.) An interesting characteristic of the filter bank used in PASC is that its sub bands are equally spaced in frequency, not in pitch. When plotted on a standard logarithmic frequency scale, like those in test reports and data sheets, the sub-bands get progressively smaller as they ascend in frequency; in Fig. 4, contrast the logarithmic frequency scale (bottom) with the PASC filter-bank bands (middle). For all three DCC sampling rates (48, 44.1, and 32 kHz), this spacing equals the Nyquist frequency (half the sampling rate) divided by 32 (the number of bands in the bank). For the 48-kHz sampling rate, there is a sub-band border every 750 Hz (750 Hz, 1.5 kHz, 2.25 kHz, 3 kHz etc.). Musical pitches are equally spaced by a constant multiplicative factor (around 6% for a semitone) and the ear hears such logarithmic spacing as "even." This is why the horizontal axis of a frequency-response chart is logarithmic. You might therefore think that splitting the signal into sub-bands equally spaced in numerical frequency, as shown in the middle of Fig. 4, would be wrong-too few bands for the lows, too many for the highs. You're actually right, but, for reasons that should become clear shortly, this doesn't turn out to be a problem. Besides, the math for logarithmic-interval filter banks is more difficult and would result in more complex and expensive PASC chips.
It is important to remember that the signals from the outputs of the 32 filter banks do not contain mere level information, as found in a spectrum-analyzer display, but contain the actual audio information from each sub-band, essentially modulated down in frequency by a factor of 32. The filter-bank outputs are still sampled signals in the digital equivalent of alternating current as seen in Fig. 5, which shows graphically the numerical outputs of the six lowest sub-bands in a selection by who else-Madonna. This illustration, derived from my home-brew computer program that performs the PASC filter bank calculations using the full list of 2,048 coefficients, contains 512 filter bank samples for each sub-band and spans about 0.37 second of real time.
Even though it's hard to tell, Madonna is still there, albeit mathematically transformed, and none of her information has been lost--yet.

---- DCC is the first audio product to use the pour of digital
signal processing to model the masking system found in human hearing.

---- Much of PASC is still secret, so you won't be able to build
your own PASC decoder from this article. I should know--I've tried.
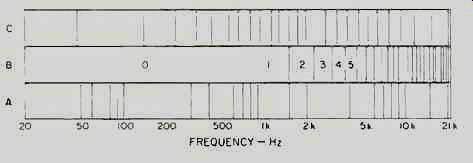
Fig. 4--While logarithmic frequency scales (bottom) correspond to our
sense of pitch, the PASC filter bands (middle) are based on linear frequency
divisions. The critical band for PASC encoding will probably resemble
the roughly third-octave critical bands used in one version of MUSICAM
(top).
Data Reduction
It is in the next step--the key stage in PASC-that information is deliberately lost and encoding artifacts are introduced. This step is the requantization of each of the 32 digital filter-bank signals of Fig. 5, as if they were again analog waveforms being converted by analog-to-digital converters. But since all the signals at this point are numerical, the requantization is done by computer math. This requantization reduces the precision-the number of bits-used to represent each sub band signal. At the filter-bank output, you recall, each of the sub-band signals is encoded with 24 bits of precision. After the requantization process, each sub-band signal is encoded, with between 15 and 0(!) bits of precision, together with a multiplicative "scale factor" that is determined by the highest level attained in each sub-band over a span of 12 consecutive samples of that sub-band.
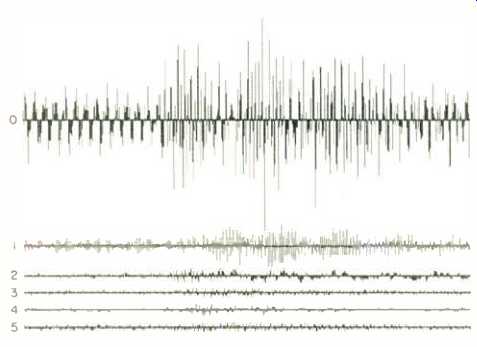
Fig. 5--Numerical outputs in 0.37 second of the six lowest sub bands
in a selection from Madonna.
Requantization with fewer bits is like taking measurements with a ruler having 1/32-inch subdivisions and then switching to one with 1/4-inch or larger gradations. Information is lost-and in electronics the loss of information about a waveform is the same as adding noise to it. During playback of a PASC-encoded DCC tape, the differences between the original 24 bit sub band signals and the fewer-bit requantized signals will survive reconversion into the analog domain and will appear as noise and distortion, both of which must be made as low as possible so as not to become audible.
In PASC, the precision allocated to each sub-band's signal can vary from one sub-band to the next and from one group of 32 sub-bands to the next in sequence. The allocation of precision is done according to the amount of noise added by the requantization process, according to the following two primary rules: First, a sub-band is re-quantized only if the signals it contains are audible to begin with (neither masked by other signals nor below the threshold of hearing). Second, the precision applied must be at least enough so that any added noise will be sufficiently masked by the music signal to be inaudible during playback. Preferably, there should be a margin as wide as possible between the added noise and the masking produced by the music. (See the second sidebar for a review of the psychoacoustical principles of thresholds and masking; for details, see F. Alton Everest's "The Filters in Our Ears," Audio, Sept. '86.) Some bands are not requantized because they carry sounds that are deemed inaudible. The requantization precision for these sub-bands is set to zero, and the "space" freed up is made available for storing bits allocated to other sub-bands. Bands carrying complex, non-masked signals will be encoded with many bits; other bands will get only a few, if any. This is why the non-logarithmic spacing of the sub bands is not all that important. With typical music, a substantial fraction of the audio signal will lie below 3 kHz, in the first few sub-bands (as in Fig. 5). These sub-bands usually will receive the dominant portion of the data stream. The remaining sub-bands, according to their contents, will get fewer bits. The bit allocations are constantly adjusted to keep the DCC audio data stream a constant 384 kilobits per second. Compare this figure to the standard DAT audio-data rate of 1,536 kilobits/S, and you'll realize how effective psychoacoustically based coding procedures can be in reducing audio storage and transmission requirements, in this case by a factor of four. (The data rates for PASC and MUSICAM are, not coincidentally, convenient ones for ISDN-the Integrated Services Digital Network-which, it is envisioned, will bring all sorts of information-age goodies into one's house via optical cable.) Philips' name for this process, Precision Adaptive Sub-band Coding (PASC) may imply to the lay reader that this is a very precise coding method. However, it would be better to say that PASC is sub-band coding that is Precision-Adaptive (note the hyphen):
The precision to which every sub-band is coded changes on an adaptive basis according to the signal content.
SIDEBAR:
The Psychoacoustics of PASC
Decades of research in psychoacoustics, the science of sound perception, have provided the two fundamental principles by which PASC can operate. These two concepts are thresholds and masking.
The most basic principle behind PASC--indeed, behind much of psychoacoustics--is the threshold, the minimum level of sound that can be heard. Thresholds are measured by isolating the listener (or subject, in psychophysics lingo) in an anechoic chamber or soundproof booth and playing sine waves or band-limited noise over headphones, or a loudspeaker. The absolute threshold is that sound level that is just detectable in the absence of all other sounds. This is the well-known threshold of hearing and it varies across the audible spectrum. It is lowest (our hearing is most sensitive) at around 3 to 4 kHz, where the absolute threshold is actually lower than 0 dB sound pressure level (0 dB SPL is just a reference sound level; it doesn't mean the absence of all sound). If a sound is below the absolute threshold, you cannot hear it even under the best conditions, and it is certainly not necessary to record it, even if microphones do pick it up. The threshold-of-hearing curve forms the lowest limit of PASC encoding; any sounds falling below it are not encoded.
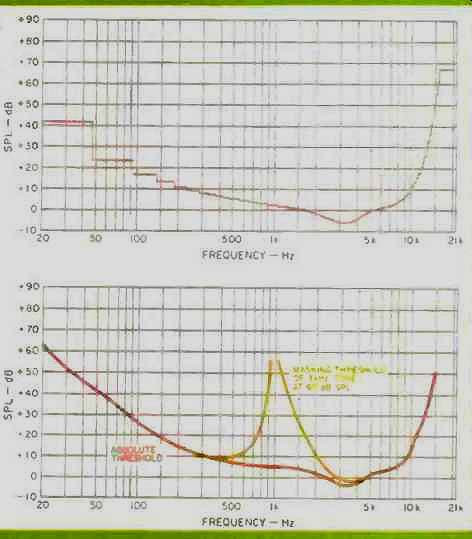
Fig. B1--The PASC absolute threshold curve will resemble this curve,
for one version of MUSICAM.
Fig. B2--Single-tone masking curve, showing how masking thresholds change in the presence of other sounds.
Figure B1 shows the absolute threshold curve used in one version of a MUSICAM encoder. While the shape of this diagram resembles the absolute threshold curve used in PASC, the two differ in several ways. PASC, for example, has its lowest and highest frequency thresholds set at 60 dB SPL, and its curve never drops below 0 dB. It is a very important phenomenon of hearing that thresholds change in response to sounds.
Even a single sine wave will raise the threshold around itself so that tones both above and below its frequency have to be louder than the absolute threshold to be detected (Fig. B2). This raising of thresholds by sounds is called masking since a low-level sound can be hidden by playing a louder sound. Masking is why a whisper that is plainly audible in a quiet room becomes inaudible at a rock concert. The sound is still there (the air molecules still move in response to the whisperer) but the loud music masks it.
An extensively studied phenomenon, masking is understood well enough for a model of it to be embedded within a PASC encoder.
The model calculates the masking produced by a music signal so as to determine what we are actually hearing in the music. Everything else doesn't need to be recorded, and in DCC it isn't.

---------- In PASC, the precision of each sub-band varies in a way
designed to minimize both noise and bit rate.
Masked information
Just how does PASC decide how many bits to allot to each sub-band? Ah, that's the secret-literally. Repeated inquiries to various Philips authorities have shown me that the "psycho acoustical model" (a MUSICAM term) used to determine bit allocation is one of the more closely held secrets of PASC, probably because the derivation of the bit allocation is the primary factor determining DCC sound quality.
Give too few bits to any sub-band, and the various masking and threshold perceptual effects that make PASC feasible may collapse, with a corresponding decline in sound quality.
Another possible reason for Philips' reluctance to talk about this portion of PASC is that any encoding scheme they describe now could later be succeeded by a sonically or electronically superior one without changing the decoding system. All that really needs to be specified in sub-band coders like PASC is the decoding scheme. In PASC, that comprises primarily the choice of scale factors, the bit-allocation method, and the input/output filter banks. A PASC encoder, which would be used only in DCC recorders, could take various forms as long as it created data arranged in a way that a standardized PASC decoder could understand. One can easily imagine there being both an extremely good and expensive encoder usable at the professional tape-duplicator level and a slightly less capable but far less costly device operating in home DCC decks.
Despite the lack of hard information from Philips on this subject, I have been assured by one Philips engineer that the following very generalized, graphically oriented interpretation (based on MUSICAM papers) is "not way off the mark" for PASC encoding as it is presently conceived.
The specific reason for the importance of the psycho-acoustical model is that it generates what is called the signal-to-mask ratio within each of the 32 sub-bands. This ratio is the distance between the sub-band's sonic contents and the masking provided by those contents, the contents of other sub-bands, or the threshold of hearing.
This signal-to-mask ratio also identifies the worst (highest) requantization noise level that is acceptable for that sub-band, for the noise could become audible if it became too loud to be masked by the music signal. The signal-to-mask ratio determines the minimum number of bits to be allocated for that sub-band: The larger the signal-to mask ratio, the more bits are needed.
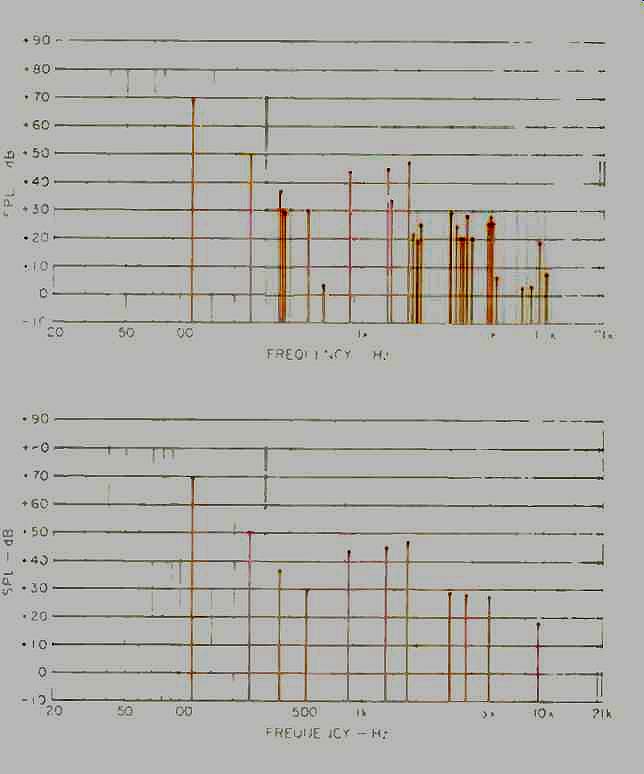
Fig. 6A--Detailed audio spectrum (FFT) before PASC encoding. Fig.
6B--Dominant spectral lines (reduced FFT ).
Now for the probable details of the process:
Step 1: Obtain a detailed spectrum (Fig. 6A). The bit-allocation scheme starts with a map-a spectrum-of the frequencies contained in the audio signal at any moment. This can be obtained by any number of methods, all of which involve digital calculations made on the incoming audio data stream. The most familiar of these methods is the fast Fourier transform (FFT). The use of an FFT is another way of compensating for the relative wideness of the lowest sub-bands, since spectral information is derived not from the sub-band contents but the psychological model's FFT. While the sub band filter divides the frequency range into 32 bands, a suitable FFT for the bit-allocation process divides the audio band into hundreds of equally spaced (in frequency, not pitch) "spectral lines." This amount of spectral detail is essential for the calculations of masking and threshold effects, because these effects occur over far narrower frequency spans than are taken in by the lowest sub-bands. Specifically, important masking and threshold effects occur across what are called critical bands, spans averaging about 1/3-octave wide across the audible range.
The critical-band boundaries specified for one version of MUSICAM were shown in the top segment of Fig. 4; you can see that several critical bands fit into the lowest filter sub-band (band 0 of the figure's middle segment). In the PASC system, the FFT's spectral lines are grouped according to their critical band.
Step 2: Find the dominant spectral lines (Fig. 6B). Next, a multi-step process removes all except the "loudest" spectral lines in each critical band.
These are then classified as to whether they are tone-like (higher than other nearby lines) or noise-like (clustered lines of approximately equal loudness). Only those spectral lines above the threshold of hearing are retained for further calculations. And since spectral lines obtained by FFT techniques become superfluously close together in the upper treble range, many of the higher frequency lines are also simply ignored.
Step 3: Calculate masking thresholds (Fig. 6C). Once the stripped-down spectrum is obtained, the masking produced by the dominant spectral lines is calculated, with each surviving spectral line producing a triangle shaped masking area whose shape depends on the line's amplitude, the critical band the line is in, and whether the sounds the line represents are tone-like or noise-like. These areas are overlaid on the absolute-threshold curve (see the second sidebar) to compute the "minimum masking threshold" (Fig. 6C). Calculate signal-to-mask ratio. For each sub-band (not critical band), the distance between the highest spectral line and the lowest minimum masking threshold in that sub-band is the signal-to-mask ratio. This marks the end of the psycho-acoustical model portion of PASC. Bit allocation occurs next. Maximize the mask-to-noise ratio.
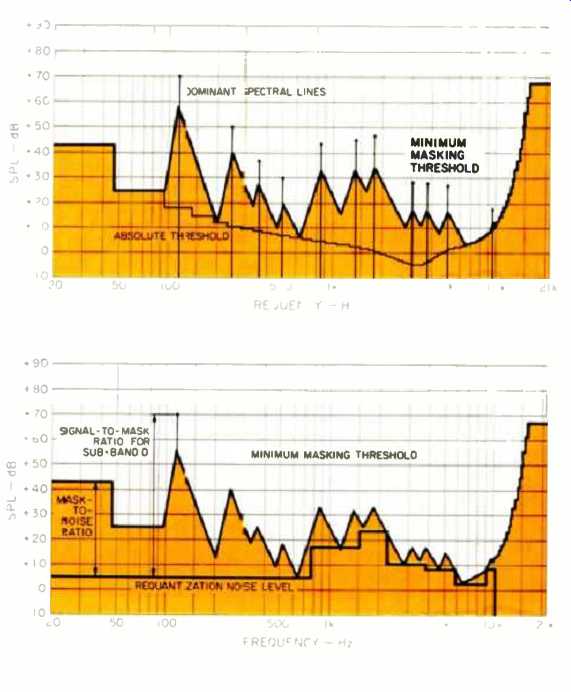
Fig. 6C--Calculated minimum masking thresholds and corresponding dominant
spectral lines. Requantization noise in the shaded areas will not he
audible. Fig. 6D--After maximizing mask-to noise ratio, remaining requantization
noise is at or well below the minimum masking threshold for each hand.
The shaded areas in Fig. 6C are the areas into which the requantization noise can be introduced without becoming audible beneath the music.
Requantization of each sub-band with fewer than 24 bits will, as mentioned before, introduce noise to the output signal. So a repetitive process is used to minimize the amount of noise (or, in other words, to maximize the mask-to noise ratio). Starting with the minimum number of bits calculated from the signal-to-mask ratio, each cycle of this process increases the number of bits allocated to each sub-band's signal until the full PASC data rate of 384 kilobits per second is reached, as shown in Fig. 6D. It is here where PASC departs from radio-oriented MUSICAM encoders, since the latter have a maximum stereo-audio data rate of 256 kilobits/S. The highest non-radio MUSICAM data rate, suitable instead for "production and professional storage," as one paper puts it, is identical to that of PASC. So it is likely that some of the "extra" data of PASC, like that incorporated into the highest MUSICAM data rate, represents an added safety margin between the requantization noise and the minimum masking threshold, so that there is an increased mask-to-noise ratio. But there may be other crucial differences between MUSICAM and PASC that Philips is keeping hidden for the moment.
Coming Out
The 384-kilobit/S data rate is not the rate at which data is actually fed to a DCC cassette. That figure is 780 kilobits per second; the difference is due to error-correction data, cueing points, and subsidiary information like that on CD (such as lyrics or graphics), and modulation to make the signal suitable for magnetic recording. Since this article is really only about PASC, I'll conveniently skip over the actual recording and readout processes.
We next meet the audio data during playback after it has been demodulated and error corrected. The data consists of basically three parts: The series of relatively slowly varying scale factors for each sub-band, the bit-allocation information that tells the PASC decoder which sub-bands have been encoded and with how many bits of precision, and the sub-band samples themselves.
The rest is fairly easy. Using the scale factor as a multiplier, each sub band sample is digitally projected into a 24-bit range and fed into the output filter bank. The output of the filter bank is, lo and behold, standard PCM "ready to convert into analog" audio when fed to a standard digital-to-analog converter (Fig. 7). But remember that, even though the samples fed into the output filter bank are 24-bit numbers, the resolution of each sample is effectively limited to that of the corresponding encoded sub-band signal. When ultimately reproduced as an analog signal, the signals in those sub-bands that actually had been recorded will have noise added beneath them. Whether that noise is audible depends on how adequately the PASC's psychoacoustical model anticipated its audibility.
This article has concentrated on masking and thresholds in PASC encoding and has ignored many other sonically relevant aspects of PASC operation such as the rate of spectrum generation or the calculation of scale factors. And it has also left uncovered some things crucially important to DCC's ultimate sonic and commercial success, such as error-correction effects, tape and head durability, and reproducibility. Of course, the big question--What does PASC sound like?--can't be answered without a critical listening test using actual PASC or DCC equipment. For Philips' sake, PASC shouldn't sound like anything at all. Despite all the processing and an output waveform that intentionally differs from the input, the goal of PASC is sonically transparent encoding and decoding.
Fig. 7--Block diagram of PASC decoder.
(source: Audio magazine, Sept. 1991)
Also see:
New Life in Cassettes--Digital Duplications (Jul. 1991)
= = = =