LEONARD FELDMAN
It’s almost become axiomatic that the music peaks in a re cording are much greater in amplitude than the average power level of a program source. This notion has enabled audio salespeople to sell amplifiers whose power output approaches the kilowatt level. It is also the reason that some speaker manufacturers have been able to boast about their systems' ability to handle short-term peaks that are 10 (20, 50, 100?) times greater than their rated maximum power handling capacity.
The difference between average and peak power levels (called crest factor) gave rise to the lab test for dynamic headroom which is part of the EIA Standard for Amplifier Measurements. In this test, a 1-kHz, full-amplitude, sinusoidal signal lasting for 20 mS is followed by 480 mS worth of the same signal, attenuated by 20 dB. A 'scope photo of this special tone-burst signal is shown in Fig. 1. By repeating the sequence over and over again, you can ascertain how much more short term power can be delivered by an amplifier or receiver than the same unit would be able to deliver on a continuous basis. The amplitude of the 20 brief alternations at high level, when clipping begins, is compared with the amplitude of a 1-kHz signal that represents the amplifier's rated continuous power output; the ratio of the two amplitudes is expressed in dB. Thus, with a dynamic headroom rating of 3 dB, the given amplifier can deliver short term power levels exactly twice as great as its continuous rated power.

The 20 mS worth of "burst" in Fig. 1 is supposed to approximate short-term music peaks, while the low-level continuous signal is supposed to represent average music signal levels. But is this contrived signal realistic? Do music peaks occur only 4% of the time (20/500 = 0.04, or 4%)? And are the differences between average and peak levels typically 20 dB? Of course, much depends upon the type of music you listen to. Studies of rock music stations reveal that the total dynamic range some of them transmit is no greater than 6 dB! On the other hand, listen to a symphony recorded by a full orchestra, and you are likely to encounter peaks more than 20 dB greater than the average level of the music and certainly much greater in level than the work's softest musical passages.
During a recent Consumer Electronics Show, I chanced upon an experiment being conducted by Denon in their exhibit space. I was attracted to the exhibit because I recognized that tie test was being performed using the Audio Precision System One, the same equipment I recently put into use in my lab. This instrument is able to measure peak and average voltages simultaneously, using its two available metering systems. In setting up a graph for this type of measurement, the X axis can be made to represent time. In Denon's experiment, the same pro gram material was sent to both metering systems (for simultaneous "peak" and "average" readings), and the test gear was programmed to take 1,000 samples over a time period of 10 minutes. This works out to about 1.67 samples per second for 600 seconds of music. One curve of the graph slowly spelled out the peak levels measured; the other curve, clearly much lower in amplitude, painted a picture of aver age levels.

I couldn't wait to repeat the experiment in my lab. I simply connected the output of one channel of my reference CD payer directly to the test gear, determined the parameters of the graph to be plotted, and chose a music se lection as a test case. Frankly, I wasn't too particular about the music, so long as it was orchestral. "Dance of the Seven Veils" from Richard Strauss' op era Salome, recorded by Delos on their Symphonic Sound Stage CD sampler (D/CD 3502), has a playing time of just over 10 minutes, so it seemed as good a choice as any.
The results are shown in Fig. 2. The curve in Fig. 2A represents peak amplitude samples during playback, while the Fig. 2B curve represents average amplitudes. Obviously, there are substantial differences in amplitude at any point along the time base, but it is not as easy to quantify the specific decibel differences at any given in stance. Happily, the test gear does more than simply plot graphs; it also stores every data point as a numeric value. These values can be retrieved at the touch of a couple of computer keys, so I printed out all 1,000 readings for both peak and average amplitudes.
One of the more significant readings occurred at 1.38 minutes into the selection. The peak amplitude read by the metering system was + 5.58 dB, and the average amplitude at the same instant was -11.70 dB--a difference between peak and average levels of 17.28 dB! A fraction of a second later, at 1.5 minutes into the selection, the peak was only + 0.84 dB. The average amplitude reading was -3.91 dB, a difference of only 4.75 dB. Another substantial difference between peak and average levels occurred at 5.5 minutes into the selection, when the peak reading was + 7.28 dB while the average reading was -10.0 dB. Once again, the difference between the two levels was 17.28 dB.

Fig. 1 – Tone burst test used in checking dynamic headroom. Signal consists
of 20 cycles of 1 kHz at full amplitude followed by 480 cycles of 1 kHz
at -20 dB.
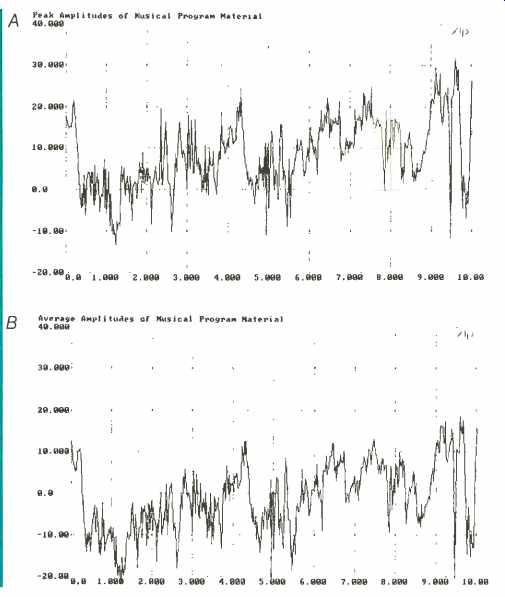
Fig. 2--Peak amplitudes (A) and average amplitudes (B) from "Dance
of the Seven Veils" on Symphonic Sound Stage CD. Test period was 10
minutes.
Scanning the hundreds of readings in the printout, I concluded that the difference between average and peak levels for this particular musical selection usually hovered between about 8 and 10 dB. Another musical selection might have yielded vastly different results; however, so long as we are talking about full orchestral works, I very much doubt it. So now we come to the bottom line of this entire experiment.
The claim that music peaks on CDs are far greater than average levels is fully substantiated. If we accept the 10-dB difference as being reasonably typical, then generally we need 10 times as much power to reproduce music peaks as we do to reproduce average levels. Of course, we haven't even taken into account the degree to which average and peak levels in a given musical selection can vary. When the speaker and amplifier makers told us that the demands of digital would mean we might have to use more powerful amplifiers and/or more efficient loudspeakers, it appears they were right after all.
(adapted from Audio magazine, Dec. 1988)
Also see: How Hot are CDs? Recording levels of CD format (July 1989)
Oberlin Smith--Centenary of Magnetic Recording (Dec. 1988)
= = = =