

New measurements of CDs show peak levels that challenge both tape and recordists.
by HOWARD A. ROBERSON
To get the best analog tape/recorder performance, recordists should know the distribution of the music's spectral peaks throughout the audio band. In the article "Basics of Tape Performance" (September 1982), I referred to two sources of information on musical spectra. A figure in that article showed the levels rolling off at about 6 dB per octave above 1, or 2 kHz. This appeared to be fortuitous, because the MOL limit (maximum output level for 3% distortion) of cassette tape fell at about the same rate, and the spectral roll-off started from the same frequency.
Although the spectral shape was a good match for analog recording, the figure was in error...I concluded that the original sources, did not include a wide enough range of musical material in one case and used a poor microphone location in the other. Considering all types of music, I could see that the high-frequency roll-offs in the spectra I was using were unrealistic. Where, then, could I get good musical spectra without spending hours making measurements of actual performances?
I decided it would be worthwhile to measure third-octave spectra from a good assortment of CDs. I selected a total of 40, most of which had received enthusiastic reviews for performance and sound quality (Table I). Music from the baroque, classical, Romantic; and other periods was selected, with an assortment of overtures, arias, and organ music. Some pop/rock and movie music was included as well. For the most part, the classical CDs are listed in the Table in order of composition.
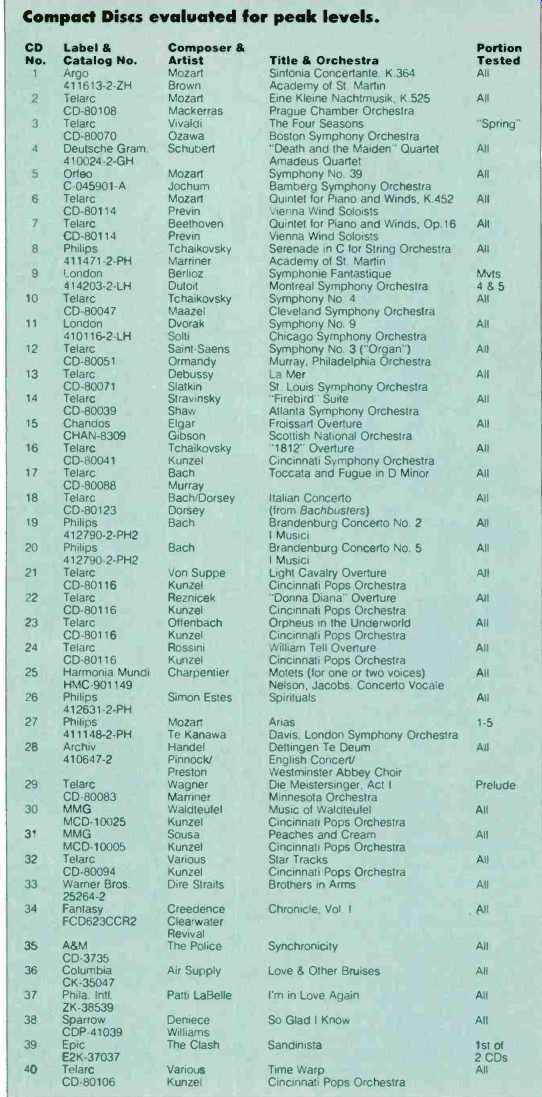
TABLE I--Compact Discs evaluated for peak levels.
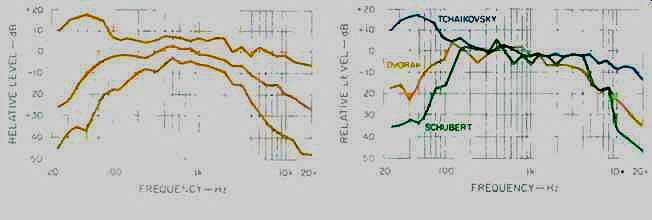
Fig. 1--Range of peak levels, in all bands, for 40 CDs. Highest recorded
peak levels for any CD are shown at top, followed by average peak levels
for all 40 discs (middle), and minimum peak levels for any CD (bottom).
Levels are shown relative to average level, from 200 Hz to 1 kHz, of
all 40 discs.
Fig. 2--Spectra of three CDs, ranked by bass content. Tchaikovsky's "1812" Overture had the highest content of the discs surveyed; Dvorák's Symphony No. 9 had median bass levels, and Schubert's "Death and the Maiden" Quartet had least bass. Plots are positioned to put their average levels (from 200 Hz to 1 kHz) on the 0-dB reference line.
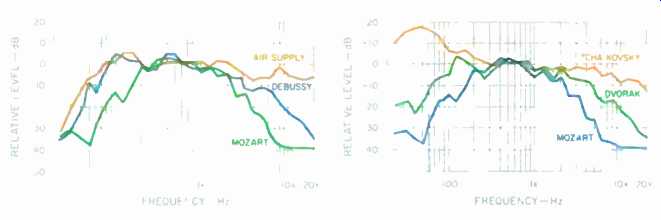
Fig. 3--Spectra of three CDs ranked by treble content, showing highest
treble content (Air Supply, Love and Other Bruises), median treble content
(Debussy, "La Mer"), and least treble content (Mozart, Quintet
for Piano and Winds).
Fig. 4--Spectra of three CDs ranked by bass and treble content, showing highest bass and treble content (Tchaikovsky, "1812" Overture), median content (Dvorák, Symphony No. 9), and least bass and treble (Mozart, Quintet for Piano and Winds).
Test Procedures
My test plan was to find the highest momentary peak levels in 30 third-octave bands (25 Hz to 20 kHz) over the duration of each piece. Peak levels of any varying musical waveform are continually changing. I wanted to get and hold the highest peak level that occurred anywhere in the music in each of the 30 third-octave bands. I used an lvie IE-30A RTA in its "Accumulate" mode to do this. The musical transients were long enough for the RTA to capture the actual peaks within a dB or so.
Maximum peak levels at the highest frequencies were caused by cymbal crashes. The highest bass levels were from organ or bass drum, except for the cannon in the "1812" Overture.
I plotted the accumulated peak levels of the CDs and of four FM pop/rock stations in each third-octave band; I then tabulated my readings. Because of variations in level from CD to CD and some changes in the measurement chain, the plotted band levels did not have a common reference. My examination of all band levels revealed that all CDs were relatively flat in the region from 200 Hz to 1 kHz. I tabulated the band levels for each CD referred to the average of its levels in the 200-, 250-, 315-, 400-, 500-, 630-, 800-, and 1000 Hz bands. Then I was able to make direct comparisons on the spectral shapes from one disc to the next.
Figure 1 shows the range of peak levels in all bands of the 40 CDs, relative to their average levels in the reference region from 200 Hz to 1 kHz. The top curve shows the highest peak levels recorded from each band, relative to the average reference-region levels of all the CDs tested. This curve shows how high the relative level might be in any one or more of the bands. The middle curve shows the average of all peak levels measured in each band; note that this curve rolls off noticeably above and below the reference region.
The bottom curve shows the lowest peak levels measured from any of the 40 CDs in each third-octave region.
This minimum-peak-level curve shows that there is some music with little bass or high-treble energy.
Figure 2 shows the spectra of three specific CDs, ranked by bass content.
The cannon in Tchaikovsky's "1812" Overture definitely generated the most bass of any CD in my test group. I judged the Dvorák Symphony No. 9 CD to have the median bass level of the group and Schubert's "Death and the Maiden" Quartet to be the CD with the least bass. A similar process was used to generate Fig. 3-for the maximum-, median-, and minimum-treble CDs--and Fig. 4, covering the same rankings for both bass and treble. The figures detail something which we all know to be true, if we consider all types of music: There is a wide range in the amount of energy in both the low- and high-frequency ends of the total music spectrum.
Spectral Envelopes
After generating these figures, I decided to try classifying the 40 peak level spectra on hand. Using trans-illumination, I traced the original spectrum plots onto graph paper. I started with the plot for CD No. 1 (Mozart's "Sinfonia Concertante") and plotted its spectral envelope. The envelopes for all other CDs were checked for possible matches. I found a number that were very similar to the Mozart disc and a few which corresponded satisfactorily, if I was willing to allow differences of a dB or two. All this music was from the baroque and classical periods, except for some vocal works.
Figure 5 shows this spectral envelope. (The CD numbers are given in the caption, so you can refer to Table I.) To get a better feel for how to meter such music, I measured the average (VU) and peak levels for pink noise, with a response shaped to match the spectral envelope. I aligned the highest level in this envelope exactly with the zero reference to show that the highest levels would be indicated accurately with peak-responding meters.
The envelope curve in Fig. 6 covers seven CDs and quite a variety of music. This envelope matched peak third octave levels for Berlioz, Dvorak, and Tchaikovsky Symphonies, Reznicek's 'Donna Diana" Overture, Debussy's "La Mer," Dorsey's Bachbusters, and four FM pop/rock stations. This envelope has more low- and high-frequency energy above 2 kHz than the one in Fig. 5.
The envelope in Fig. 7, for three works with organ, shows the major influence of the low organ notes, the highest levels of which are centered around 50 Hz. The organ in Time Warp is excerpted from "Also Sprach Zarathustra" by Strauss. Although the levels were highest below 70 Hz, the low frequency peak levels were easy to meter correctly. The envelope of Fig. 8 covers Stravinsky's "Firebird" Suite and four overtures. The highest levels were from the bass drum, but there was considerable energy across the entire audio band. Some care was needed+ to catch the peak levels from the drum beats, but it was a relatively small adjustment and easily made.
Figure 9 shows the spectral envelope generated by the music of Waldteufel and Sousa. Both of these CDs have sudden bass drum peaks (visible on the envelope). My checks indicated that if a recordist were setting input gain based on signal levels elsewhere it these recordings, his levels would probably be about 2 dB high on these drum peaks. The music from Star Tracks and Brothers in Arms (Fig. 10) had a wide and quite flat peak spectrum before a roll-off at around 10 kHz.
Accurate metering was easy with these sources.
Figure 11 revealed a close correspondence in peak spectra among six pop/rock CDs. Because of the general steadiness in the peak level and the wide high-level spectrum, the recordist would probably set the level slightly low. On the other hand, the cannon shots in Tchaikovsky's "1812" Overture (Fig. 12) would be very hard to meter correctly, and thus over-recording would be very likely.
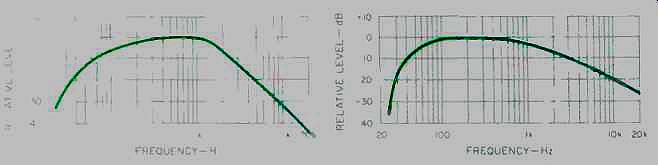
Fig. 5--Peak-level spectral envelope, with highest level used as 0-dB
reference, for classical and baroque music plus vocal solos and choral
works. The discs are listed in Table I as CDs 1 to 8, 19, 20, and 25
to 28.
Fig. 6--Peak-level spectral envelope for symphonies, overtures, and other classical works (CDs 9, 10, 11, 13, 18, 22, and 29) plus pop/rock FM stations; see text.
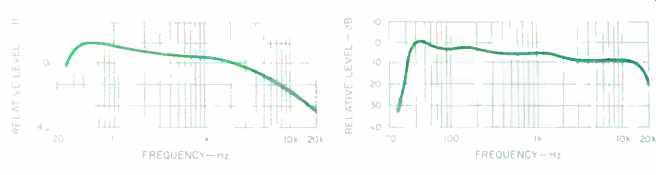
Fig. 7--Peak-level spectral envelope for works with organ (Saint-Satins,
Symphony No. 3; Bach, Toccata and Fugue in D Minor, and Strauss, "Also
Sprach Zarathustra"), listed in Table I as CDs 12, 17, and 40.
Fig. 8--Peak-level spectral envelope for overtures (CDs 15, 21, 23,
and 24) and Stravinsky's "Firebird" Suite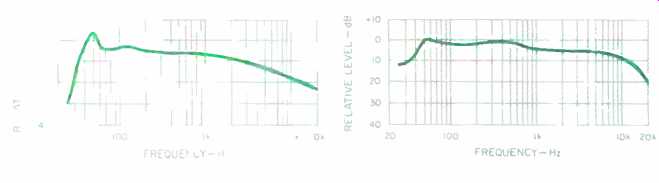
Fig. 9--Peak-level spectral envelope for music of Waldteufel and Sousa (CDs 30 and 31). The peak at 50 Hz is from bass drum beats; see text.
Fig. 10-Peak-level spectral envelope for music from Star Tracks any Brothers in Arms (CDs 32 and 33).
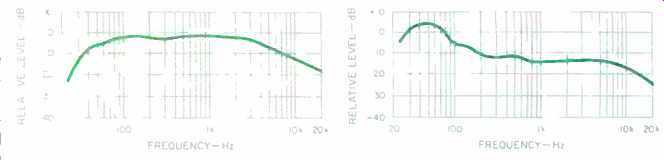
Fig. 11--Peak-level spectral envelope for pop/rock music (CDs 34 to
39).
Fig. 12--Peak-level spectral envelope for Tchaikovsky's "1812" Overture (CD 16).
Metering, EQ, and MOLs
Peak-responding meters on most decks are fast enough (less than 20 mS) to show typical musical transients, but they read the signals before record equalization, with its high-frequency boost, is applied. As a result, some high-frequency distortion and saturation might be occurring without the meters giving any warning of it. Because of the general level roll-off in the higher frequencies for all music, however, there usually would be little change in the peak meter indications even if the meters were reading the equalized signal. Indications for average-responding (VU-type) meters were usually 8 to 10 dB below those for typical recorder peak-responding meters.
When the levels were measured with an absolute-peak meter, which can display fast transients, they were at least 14 to 15 dB above the indications on the VU meters. Because of the very short duration of these instantaneous peaks (less than 200 µS), distortion would probably not be heard if they were slightly above the MOL limit.
These figures, however, should help emphasize that when using a VU-type meter, the recordist must allow at least 10 dB of headroom to get low-distortion recording.
The fall-off in tape MOLs above 1 kHz is well known. If there was no record (or playback) equalization, the high-frequency MOLs would drop relatively little-but the noise would go up.
The cassette format is locked into 70 and 120-µS equalizations. A small number of decks allow switching equalization separately, regardless of tape type; this can be helpful, as I will show later. Open-reel recorders, at tape speeds of 3 3/4 and 7 1/2 ips, may use as much record-equalization boost as do cassette recorders. At the higher tape speeds, particularly 30 ips, the required boost for open-reel recording is significantly less.
Figures 13, 14, and 15 show the range of MOLs, without noise reduction, using a Nakamichi CR-7A deck for the 35 tapes covered in my last tape survey (November 1987). The dashed lines at the low-frequency ends of the curves show the drop in MOLs from 100 to 50 Hz for the typical deck. The best decks, in this regard, have about a 2-dB drop, and the worst decks have about a 10-dB reduction in MOLs from 100 to 50 Hz. At 40 Hz, the reduction in performance for all decks is even greater. The Type I MOLs are shown in Fig. 13, the Type IIs are in Fig. 14, and those for Type IV are in Fig. 15. In these figures, the top curve for each tape type is for the best MOLs, and the bottom curve is for the worst MOLs.
When I re-plotted some of this MOL data, I had to conclude that there was too great a discontinuity between the distortion levels shown at frequencies up to 1 kHz (where I measure third order harmonic distortion) and from 2 kHz up (where the tape's frequency limits force me to use third-order twin tone IM measurements; see sidebar).. The reference level I had been using for the twin-tone IM tests was based on the rms levels of those tones, as specified by an IEC Standard I was using. However, DIN Standard 45 403, for nonlinear distortion measurements, clearly states that peak level is the proper reference. Careful examination of distortion products, with a spectrum analyzer, provided real-world confirmation. The peak level of twin tones, with each one at the same level, is 6 dB higher than a single tone and 3 dB higher than the twin-tone rms level.
Figures 16, 17, and 18 show the effect of this necessary adjustment with the twin-tone IM MOL curves raised 3 dB. (Twin-tone IM data, in the earlier survey, should be increased 3 dB as well. Relative tape rankings remain the same.) The little jog that remains with Type II (middle) and IV (bottom) tapes is correct for the standard 70-uS equalization. The dashed line above the Type II and IV MOL curves, above 1 kHz, shows the MOL increase that 120-uS equalization would yield.
=================
DISTORTION TESTS & ANALOG RECORDING
In general, measuring harmonic distortion is straightforward. There are many low-distortion sources these days, and analyzers are available in a number of formats. Tape noise in analog recording, however, makes it difficult to get reliable distortion data unless the recorded flux level is above 50 nW'b/m or so. If 3% distortion is the criterion, the levels will be much higher and harmonic distortion is easily measured--particularly at lower frequencies.
The distortion in analog tape recording is primarily third-order, and the third harmonic s the most prominent in the playback of a single recorded tone.
Accurate assessment of third-order distortion, in general, requires flat record/ playback response out to the frequency of the third harmonic. When the record levels are high enough to cause 3% distortion, however, the response on a typical deck begins falling off by 1 kHz.
Data taken at higher frequencies is valid for assessing harmonic distortion, but third-order distortion involves more than simple harmonics. Complex musical energy around the same frequency and at the same level would cause many combinations of sum-and-difference frequency distortion products. In other words, measuring the harmonic distortion of a single tone is not adequate for assessing nonlinear performance with music-except at lower frequencies.
A two-tone test signal can be used for tests out to the response limits of the deck, as its difference-distortion products remain in band. The third-order difference products for two tones f1 and f2, are:
f3 = 2f, f2
and f4=2f2-f1
Another way of stating these frequency relationships is:
f3 = f1- (f2-f1) and
f1=f2+ (f2-f1).
There are also two sum products:
2f, + f2 = 3f, + (f2 – f1) and
2f2 + f1 = 3f2 (f2 - f1),
which show their frequency grouping with the third harmonics.
Figure B1 shows the waveform of a 500and 600-Hz twin-tone signal. Each individual tone was four divisions high, peak to peak, but the combination is almost eight divisions high. This doubling of peak levels holds true for all combinations of frequencies. Figure B2 is the spectral display of the fundamentals and the distortion in the playback from a Nakamichi CR-7A deck.
The level reference is the peak level of the two tones, which is 6 dB above the level of each fundamental.
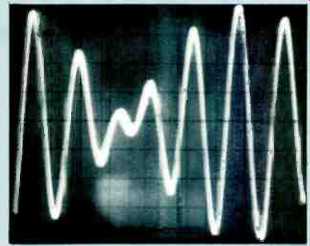
Fig. B1--Waveform of 500and 600-Hz test signal.
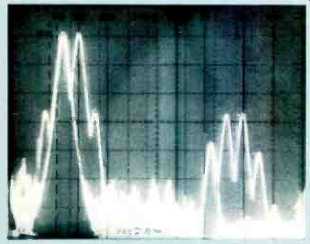
Fig. B2--Third-order distortion products. At left are 500- and 600-Hz
fundamentals, flanked by third-order difference products. At right are
third harmonic of 500-Hz fundamental (1,500 Hz), third-order sum products
of 500 and 600 Hz. and third harmonic of 600 Hz (1,800 Hz). Scales: Horizontal,
200 Hz-/div.; vertical, 10 dB/div.
Two sweeps were actually made with the analyzer: One with just the 500-Hz signal and the other with both tones.
Notice that the 1,500-Hz third-harmonic distortion product stays the same in level when the second tone is added. Also note hew much higher the difference and sum distortion products are in comparison to the harmonic distortion product. The great difference between the amplitudes of the harmonic and IM distortion products is due to the 6-dB increase in the effective recording level when the second tone Is added. When single-tone and twin tone peak levels are the same, the overall third-order distortion levels are the same. As the test-tone frequency increases, the levels of the third-order harmonic and sum distortion products are reduced more and more, relative to the level of the difference-frequency products.
With close spacing between the fundamentals, f1 and f2, their output levels will be almost identical, as will the levels of f3 and f1, the third-order difference frequencies. As a result, distortion tests are possible almost to the very response limit of the deck. Music s made up of many more frequencies than lust two, but twin-tone testing allows exercising a deck's entire audio band.
--H.A.R.
=================
I thought that the MOL curves should provide a level-limiting curve for the spectral envelopes. I did have some question about what happened at all frequencies with broadband signals. I used a Type I tape with the Nakamichi CR-7A deck and ran a compression test with pink noise. The first test here used flat pink noise (20-kHz roll-off), with the input level adjusted in 1-dB steps from-10 to +20 dB relative to meter zero. I used a special dual attenuator, with one section increasing input level and the other section decreasing playback level. In this way, the level to the RTA was constant except for effects from compression.
The bottom trace of Fig. 19 shows the result of this test. The flat upper edge of the trace shows the flat frequency response obtained when recording at-10 dB; the bottom edge shows the response when recording at +20, where output was actually lowered due to compression/saturation.
Notice how much greater this effect was at the highest frequencies than at 2 kHz and below.
For the next test, I used equalization to shape the pink noise to match the MOLs for the particular tape and recorder in use. The top trace of Fig. 19 shows the result of adjusting the input over the same meter range, from 10 to +20 dB relative to meter zero. With this shaping of the "music" to match the MOL limit across the whole band, the compression was very much the same in each of the 30 third-octave bands, as shown by the close parallel between the upper and lower edges of the trace.
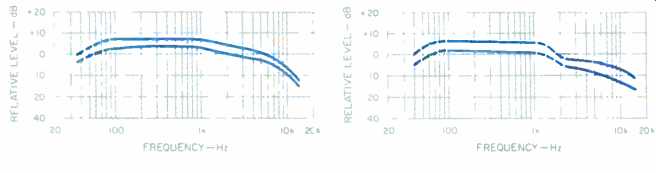
Fig. 13---Range of MOLs for 3% distortion for 13 IEC Type I tapes. High-frequency
MOLs shown are referred to rms level of twin-tone signal re: Dolby level;
see text.
Fig. 14-Same as Fig. 13 but for 15 Type II tapes.
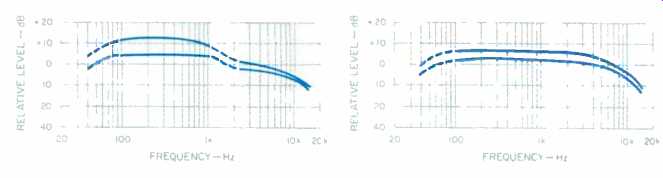
Fig. 15--Same as Fig. 13 but for seven Type IV tapes.
Fig. 16--Range of MOLs for 3% distortion for 13 IEC Type I tapes. High-frequency MOLs shown are referred to peak level of twin-tone signal re: Dolby level; see text.
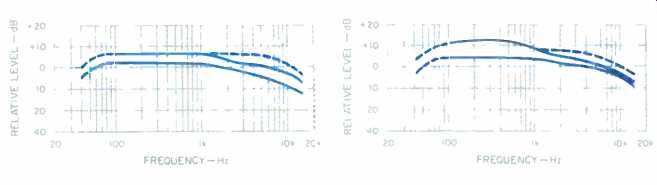
Fig. 17--Same as Fig. 16 but for 15 Type II tapes.
Fig. 18--Same as Fig. 16 but for seven Type IV tapes.
The next step was to overlay the MOL curves on the eight spectral envelopes (from Figs. 5 through 12) for guidance on what record levels would be possible. The guidelines given here assume the meters are peak responding, with the level first set to match the 400-Hz MOL figure. In this case, there would be a downward level adjustment to prevent any part of the envelope from protruding above the MOL limit.
Figures 20 and 21 demonstrate how I did this. The top curve in each of these two figures is the best MOL curve for Type I tapes from Fig. 16. The bottom curve in Fig. 20 is the peak level spectral envelope from Fig. 7. Notice how low the recording level would have to be set to prevent distortion at 40 Hz. Figure 21 shows that there is a better match to the deck/tape's MOLs with the envelope from Fig. 11. The actual limit occurs slightly above 15 kHz. Pushing the level higher, until this envelope intersected the MOL curve at 15 kHz, would not generate much in band harmonic distortion products.
But there would be high-level, third order, difference-tone IM distortion products that would be in band.
Table II lists the required dB corrections in maximum meter readings relative to the 400-Hz MOL limit, to prevent noticeable distortion anywhere else in the entire band. The Table shows where the MOL limit occurs and gives the results for both the best and the worst MOLs shown in Figs. 16, 17, and 18. The envelopes in Figs. 5 and 6 show a concentration of energy in the middle of the music spectrum. The required adjustments, in most cases, are relatively small. The high level of the low organ notes (Fig. 7) requires a sizable reduction in the overall recording level to limit distortion. The spectrum is flatter in Fig. 8, but the required reductions are also large in all cases.
The high-level drum beats at 50 Hz (Fig. 9) would be hard to catch, and a large level reduction is required here also. The reductions are somewhat less with the envelope shown in Fig. 10, but they are important, reaching limits at one end of the spectrum or the other, depending on the shape of the MOL curve. The pop/rock CDs (Fig. 11) have peak band levels that are flat for most of the audio band but roll off at the extremes. For this type of music, the recordist needs to make some downward adjustment, but less than would be necessary for a number of other types of music. The required compensation for the cannon shots in the "1812" Overture (Fig. 12) cannot be defined as accurately as for the other envelopes. But it appears that the maximum meter level should be about 10 dB lower than the 400-Hz MOL limit for the tape/recorder used.
If the audiophile sets his goal to be the prevention of 3% distortion at any time, even on a single peak or two, the adjustments of level listed in Table II are musts. For lower quality decks, the reductions should actually be greater.
If we consider how great some of the reductions should be, it is quite discouraging. It just won't seem right to set the levels to less than meter zero on peak-responding meters, and even lower on VU-type meters. Some of the envelopes require this, however, and the distortion will be low. Let me suggest that the envelopes and Table II provide guidelines which point out where distortion will start with increasing record levels. By all means, the recordist should listen carefully, for it may be difficult to accept noise that goes with really low distortion.
Interesting details can be gleaned from the Table. For example, notice that with Fig. 11 the limit for Type II and IV tapes is not at the frequency extremes but at 2.5 or 3.0 kHz. Notice also that in many cases-and especially when using the Type IV tapes-a greater adjustment is needed for the tapes with the best, as opposed to the worst, MOLs. This is the result of the shape of the MOL curves: The best MOL curves drop off noticeably from low to high frequencies, but the worst MOL curves are relatively flat.
The use of 120-4 equalization with Type II and IV tapes (see Figs. 17 and 18) did not provide as much of an advantage as I had thought it would.
There was really no advantage in an equalization change for the envelopes in Figs. 5, 6, 7, 9, and 12. The improvement in record level for high-MOL Type IVs was 3 dB for the envelope of Fig. 8 and 3.5 dB for the envelope of Fig. 10.
The improvement was about 2 dB for both Type II and IV tapes with the envelope of Fig. 11.
All of the preceding material relating to tape/recorder performance has been for operation without noise reduction. What will noise reduction do to help remove at least some o' the limitations discussed here? First, set's take a look at what Dolby C NR might do. In the past, I have shown many high-level responses, especially for swept sine waves, that evidenced obvious and worthwhile headroom extension with Dolby C NR. After learning more about the limitations of falling high-frequency MOLs, I had to wonder about the extent of the effects of this NR in actual recording. The first thing I did was to check what the meter indications were for a Dolby-level calibration tape and then for pink noise at the same rms output voltage. The Dolby level from the tape read correctly at meter zero, but the deck's peak-responding meters bounced between +4 and +7 dB with the pink noise.
I then looked at record/playback response-with Dolby C NR, over a range of levels with pink noise-both flat and with response shelved at-5 dB above 3 kHz. While looking at playback after rewinding, I switched the NR in and out, both to see the result with NR and to check what the encoder responses were at these levels.
There was some anti-saturation shaping of the encoder response, starting just above Dolby level.
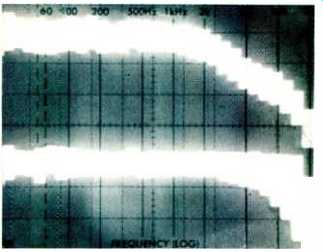
Fig. 19--Compression test using Type I tape on Nakamichi CR-7A. Record
level was varied in 1-dB steps from -10 to +20 dB. With normal pink noise
(bottom trace), response was flat at low recording levels (upper edge
of trace) but compressed at higher levels (lower edge), especially at
higher frequencies. With pink noise shaped to match the MOL curve (top
trace), frequency response of uncompressed signals (upper edge) and saturation-compressed
signals (lower edge) was almost the same. Vertical scale: 5 dB/div.
TABLE II--Required corrections to maximum record level allowable (400-Hz
MOL reference) to limit distortion.
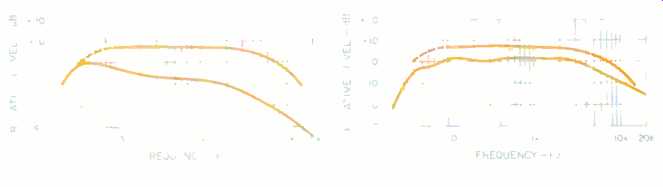
Fig. 20--Comparison of peak spectrum envelope of organ music (Fig. 7)
with Type I, best MOL curve shows that low-distortion recording limit
occurs at 40 Hz.
Fig. 21--Comparison of peak spectrum envelope for pop/rock music (Fig. 11) with Type I, best MOL curve shows low-distortion limit at 15 kHz.
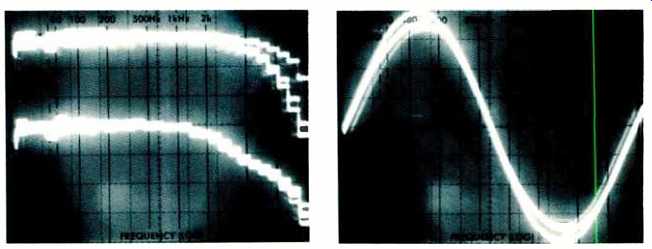
Fig. 22--Effects of Dolby NR on response at +20 dB recording level for
flat pink-noise input (top trace) and MOL-shaped pink noise (bottom trace).
Where traces split, at right, upper portion is with Dolby C NR, middle
portion is without NR, and lower portion is with Dolby B NR; see text.
Vertical scale: 5 dB/div.
Fig. 23--Shape of playback sine wave with low distortion (larger trace) and with 3% distortion (smaller trace); see text.
Figure 22 shows record/playback responses using pink noise with a very high record level. The responses shown in the top trace resulted from using flat pink noise. The response without NR is the middle portion of this trace. Dolby B NR caused a somewhat greater roll-off at the highest frequencies, but Dolby C NR secured a very obvious reduction of the roll-off. The responses shown in the bottom trace . = are from using pink noise rolled off to match the tape/recorder MOL curve.
The record level was increased to match that for flat pink noise. Even with this rolled-off signal, switching to Dolby C NR is somewhat helpful here. I should note that these tests do not recreate any particular music condition and just indicate the benefit of anti saturation.
In a tape deck having dbx II NR, the compansion system's zero-gain point should be set at about-10 dB or perhaps slightly lower. When this is done, dbx II NR would help in preventing high distortion with most of the spectral envelopes shown. For some recorders in particular, however, dbx II NR has shown rather high distortion and rolled-off response in the region of low organ notes and bass drum beats.
Post-playback equalization might help correct the roll-off in some of these cases.
Some readers might like to find where the 400-Hz, 3% distortion point is just by looking at the playback waveform. Figure 23 shows how this can be done. There are two overlaid waveforms: The good sine wave is from the signal source, and the squashed one is from the deck playback. To show this, you need a signal source (around 400 Hz is best) and a two-channel oscilloscope. The oscilloscope should have combination synchronization so that both the source and playback waveforms (which are read at slightly different times) can be aligned.
The source-waveform gain is set to make it fill the full eight divisions. The gain for playback is adjusted to make its waveform match the source waveform as exactly as possible over the straighter portions, with some vertical positioning perhaps needed for accurate alignment. The distortion is quite close to 3% when the playback waveform is squashed half a division at both top and bottom. This is not an exact indication, but it will help to define reference levels.
It is good for the recordist to know where on the meters the low-frequency (250 to 400 Hz), 3% distortion limit is for each of the tape formulations used.
This article is a first try at obtaining a better understanding of the range of peak-level spectral envelopes for many types of music. With continuing examination of additional CDs, I may find a need for other envelopes. On the other hand, the envelope in Fig. 7 is somewhat similar to that of Fig. 9, and the levels of the envelope in Fig. 12 are close to matching those at the frequency extremes in both Figs. 7 and 9.
The MOL curves which have accompanied my Audio tape tests are based on a 3%, third-order distortion limit, measuring harmonic distortion for the lower frequencies and twin-tone difference distortion for the higher frequencies. Of course, 3% is certainly not a low level of distortion. In some of my own listening, I thought that the results were much better when I limited the record level to what would amount to about 1% distortion, as indicated on peak-responding meters; this level limit would be 5 dB lower than the MOL criterion. Now that I have looked at the various spectral envelopes, I will be more discerning about what to expect.
What I thought was my 1% distortion, peak-meter limit may really be close to a 3% limit for momentary peaks at any point in the band.
I do hope this discussion will help recordists become more aware of the challenges provided by various types of music. In digital recording with either R-DAT or PCM, the exact spectral shapes are less important, but good recording practice is still required to ensure that sudden peaks do not drive the system into overload. Primarily, these guidelines should help you find the best record-level settings for the various possible analog tape/recorder combinations.
(adapted from Audio magazine, July 1989)
Also see:
A New CD Test Standard (Dec. 1985)
Crest Factors of CDs (Dec. 1988)
Thomson CD Recorder -- Exclusive U.S. Test!!! (Mar. 1990)
Bit By Bit (AES presentation, “Audio in Digital Times”, May 1989) (Sept. 1989)
= = = =