by D.W. FOSTLE
[D. W. Fostle is the author of The Steinway Saga (Scribner, 1995). His techniques for computer-based measurement of musical signals, developed in researching that book, form the basis of this article. For their technical services in making the test recordings, the author wishes to thank Marc Aubort, Elite Recordings; Jerry Bruck, Posthorn Recording; Keith Johnson, Pacific Microsonics; and Chris Rice. A debt is also owed to pianist Jerome Lowenthal, producer Joanna Nickrenz, and piano tuner Tali Mahanor, who prepared "Penelope" (a.k.a. Steinway Model D, 56 290).]
NEW RECORDING TECHNOLOGIES SUCH AS NOISE SHAPING AND HDCD PROMISE MUCH, BUT DO THEY REALLY LIVE UP TO THEIR HYPE-AND ARE THERE BETTER ALTERNATIVES?
In last month's examination of 20-to-16-bit noise-shaping techniques ("19 Bits in a 16-Bit Sack?"), real musical signals recorded on practical systems were shown to contain enough noise to swamp the effect of the noise-shaping filters. Recordings with noise floors approaching even the 16-bit theoretical limit, without noise shaping, prove to be rare, and it can be safely stated that the "19-bit equivalent" performance predicted by both digital theoreticians and advertising copywriters has not yet been achieved.
If noise shapers as a class are typically defeated by noise in the signals on which they operate, the question arises as to whether their use is otherwise benign. Do these de vices alter the musical information that passes through them, or are their operations confined solely, if largely ineffectively, to noise? To gain insight into the issue, 20-bit "test" recordings were made. Assembled was a high-quality recording system comprising two Schoeps CM-65 microphones with 958 capsules, a Hardy M-1 micro phone preamplifier, a Wadia Digital 4000 20-bit analog-to-digital (A/D) converter, and a Nagra D 20-bit digital recorder. With this system, Marc Aubort recorded performances by Jerome Lowenthal, a concert pianist and chairman of the Juilliard School piano department.
The main purpose of the recordings was to document the amazing variety of timbres and musical effects produced by Steinway pianos built over a period of 140 years, but the 20-bit masters also provided material having low noise, a musical dynamic range in excess of 60 dB, a complex reverberant field, and daunting transients. Some piano attacks contained instantaneous energy beyond 20 kHz, and even at moderate levels, "sprays" of energy up to 16 kHz were commonly measured.
Noise Shaping or Sound Shaping
To audit and measure the effects of the noise shapers, I created a 20-bit edited master on a digital workstation and then transferred it back to the Nagra D. Using the Nagra's built-in error-logging facilities, I monitored digital error rates and found none. I then used the edited 20-bit data, now on tape, as a source to feed each of several noise-shaping devices (a Weiss SFC-1, a Meridian 618, and a Sony K-1203), whose outputs were transferred to a Marantz CD recorder.
The final result was a CD, playable on any system, that contained the various noise-shaped versions of the original 20-bit recording. On audition, I found that the different noise shapers yielded differences in instrumental timbre, reverberation color, and stereo presentation of the piano. As a class, the noise shapers tended to "harden" or "brighten" the sound, particularly in the reverberant decay. Though difficult to de scribe, the effect was similar to that of in creasing the area of the performance space covered with plaster or stone and reducing the area covered with wood. The timbral corollary of this is a "brightening" of the piano, particularly in the top two octaves.
That the noise-shaping filter plays a role in these effects can be demonstrated with the Meridian 618, which has several increasingly powerful noise-shaping selections. Moving from the milder to the steeper curves causes a progressive brightening of both the piano and the reverberant field.
The noise-shaping devices also influenced the stereo image, sometimes in unexpected ways. The apparent size of the piano was noticeably smaller with the Sony Super Bit Mapping (SBM) processor than with other processors. This could be described as a more defined image or, if one does not prefer a smaller piano, as a reduction in scale. I also noticed that the Weiss SFC-1 seemed to "push" reverberation toward the speakers when compared with the other noise shapers.
There remained the question of how re producible these effects would be on other systems in other rooms. To explore that is sue, the comparison CD was auditioned through the same digital-to-analog (D/A) converter on two other systems, both owned by audio professionals. Although rendered differently in degree, the effects were sustained. The most robust effects were on piano timbre and the general brightening of reverberation. Stereo presentation, while consistent in direction, had markedly different scale among the three systems. (And in general, the sonic differences among the noise shapers were much smaller than the variations among the systems on which the recordings were played.) A specific and measurable case can be seen in Fig. 1, a spectrogram of the piano-attack transient produced after passage through the Sony K-1203 SBM processor.
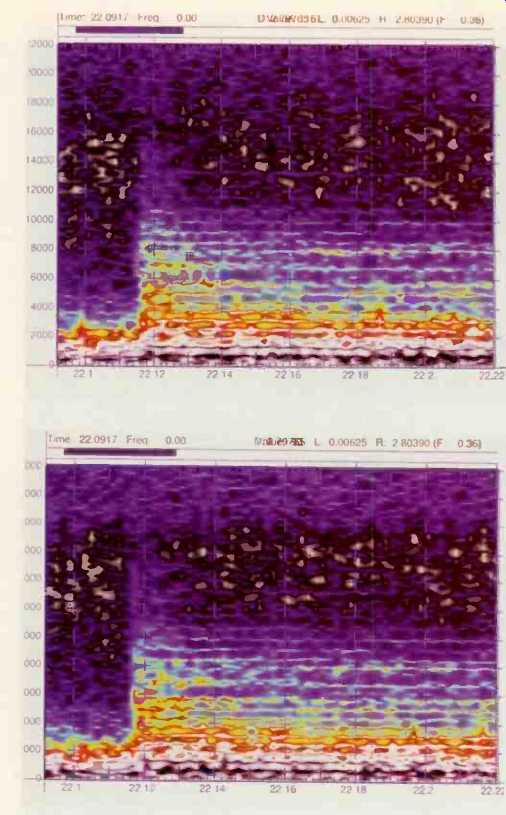
Fig. 1--"Three dimensional" spectrogram of a piano-attack transient
after passage through a Sony K-1203 SBM noise shaper. Time is charted horizontally
in seconds, frequency vertically in hertz; amplitude is indicated by color
(see color key below). Note the slight bulge, or "puff," from the
left edge of the attack's vertical structure, between about 6 and 8.8 kHz.
Fig. 2--Spectrogram of the same piano attack in Fig. 1, this time processed through an Apogee UV-1000, which uses the company's UV-22 20-to-16-bit redithering process but no noise shaping. The slight "puff" of energy visible in Fig. 1, ahead of the attack, is absent here.
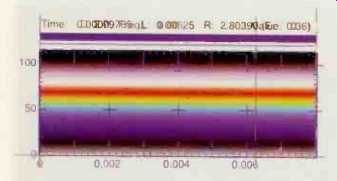
The single, sharply struck mid-treble note, with a peak level 11.9 dB below digital full scale (0 dBFS), pops from a softly played bass figure in Paderewski's Minuet in G.
Note the "puff" of energy between 6 and 8.8 kHz prior to the main attack's vertical structure. This manifests itself as something like a click, the reproduction of which was found to depend on the playback system.
On one system the puff was very sharply rendered, producing a sound similar to an instantaneous digital overload, a clear impossibility given the levels involved. On another playback system a light tick was heard, which could easily be confused with the click of the artist's fingernail accidentally contacting a piano key. On a third play back system the puff emerged as a low-level "thock" sound, which, in that instance, listeners might well have identified as a sticking piano action or as other mechanical noise from the instrument itself.
When the same signal is passed through a processor that doesn't use noise shaping, in this case the Apogee Electronics UV-1000, the puff is absent and there is better overall alignment of the attack transient. The Apogee's reproduction of the attack can be seen in Fig. 2. The puff is an artifact produced by the SBM processor and was not present on the master recording when played back directly from the original 20-bit tape. Since each playback system rendered the artifact differently, listeners could easily come to different conclusions as to its cause. Without reference to alternative 16-bit masterings through other processors or a 20-bit original, the listener would not realize the sound was actually created by a noise-shaping process.
Caution is in order, however, with regard to generalizing from these observations. They emerged from experiments with only one class of program material, and a particularly daunting one at that. A signal having less natural reverberation would make it harder to distinguish between the various noise shapers. And the alterations to stereo phonic imaging would likely have been reduced, if not obliterated, had more than a simple stereo pair of microphones been used, as is sometimes done even on classical piano recordings and which is the essence of multitrack recording.
It is nonetheless evident that noise shaping can have sonic effects, and those effects may alter not merely the noise floor but other aspects of the presentation as well. Of those detected, the alterations of the piano's timbre and attack transients are perhaps the most important musically. Classical pianists are judged, in part, by their "touch" and their "tone," both of which can be modified by effects such as those introduced by the noise shapers. Since the general tendency of the process is to harden transients and brighten the overall piano sound (the two phenomena are correlated in the instrument), it is possible that subtleties of musical meaning or judgments of artistic capacity will be altered. That is not necessarily adverse; for example, the effect of transient "sharpening" might be to increase the definition of individual notes in a complex musical passage.
But any such aesthetic application of a noise shaper, which effectively transforms it into a very peculiar form of equalizer, is separate from its design goal.
The connection between equalization and noise shaping is not as farfetched as it might seem, noise shapers being a specialized permutation of a larger class of devices that includes equalizers and tone controls.
In fact, the well-known tendency of filters to "ring" may possibly be relevant. Since the shapers examined can introduce alterations of 20 to 50 dB in the signal, it seems possible that they may alter transient wave form shapes. I advance this notion not as a finding but as an informal speculation as to the physical cause of some of the phenomena heard. Whatever the reason, however, it appears that noise shapers can, at least under some conditions, "shape" music as well.
The Apogee Alternative
One special alternative to noise shaping in converting 20-bit masters to 16-bit CDs is Apogee Electronics' UV-22 redithering system, incorporated in the company's UV-1000 mastering processor and, more recently, as a built-in function in its 20-bit A/D converter. Apogee reports wide adoption of the UV-1000 in mastering facilities.

Intended as a "final step" mastering processor, the UV-1000, like some of the other de vices examined, has other capabilities. In the case of the UV-1000, they include DC-offset removal, signal generation, left/right channel reversal, and an ability to slightly reduce digital signal levels to prevent overload.
In the UV-1000's manual, Apogee says that the UV-22 process "adds an inaudible, -frequency 'bias' to the digit bit stream, placing an algorithmically-generated 'clump' of energy around 22 kHz." Figure 3 shows the spectrum of the Apogee's output (green curve) in comparison to that of the Meridian 618's "flat dither" (red curve).
Until about 14 kHz, the Apogee's noise level is 4 to 5 dB below that of conventional dither. This is generally consistent with Apogee's claim that the process's noise floor is the same as the theoretical 16-bit minimum. By 16.5 kHz the energy in the Apogee's output is equal to that of the Meridian, and the small peak at 19.5 kHz is about 23 dB above the Meridian's noise. A second peak occurs at 20.9 kHz and a third, smaller peak at 21.8 kHz.
Apogee's claim that UV-22 is "not a new flavor of dither noise" is confirmed by Fig. 4, a spectrogram of 1 second of the UV-22 signal. It shows multiple frequency modulations that, over time, tend to center at the spectral peaks of Fig. 3 but vary as much as 1 kHz in either direction. If this signal were conventional random-noise dither, the spectrogram would show only small lacy patterns of blue and white. Underlying this unusual signal is a very complex, statistically based theory (not entirely explained in published papers) as well as extensive listening tests. The question is, does UV-22 work?
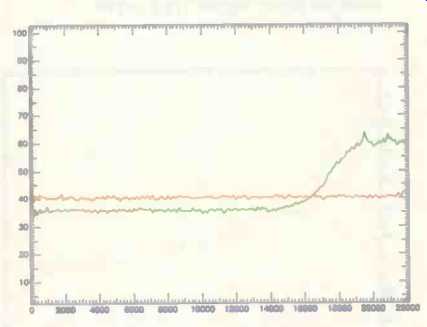
Fig. 3--Spectrum of the Apogee UV-1000 processor's noise floor (green curve)
compared with that of the Meridian 618 mastering processor in its "flat
dither" mode (red curve).
The bulge in the Apogee spectrum at extremely high frequencies results from its concentration of dither energy in the near-ultrasonic range, which reduces noise at lower frequencies. (As on most of the amplitude-versus-frequency graphs, the decibel scale to the left is strictly for evaluation of relative levels and is not based on any absolute reference.)
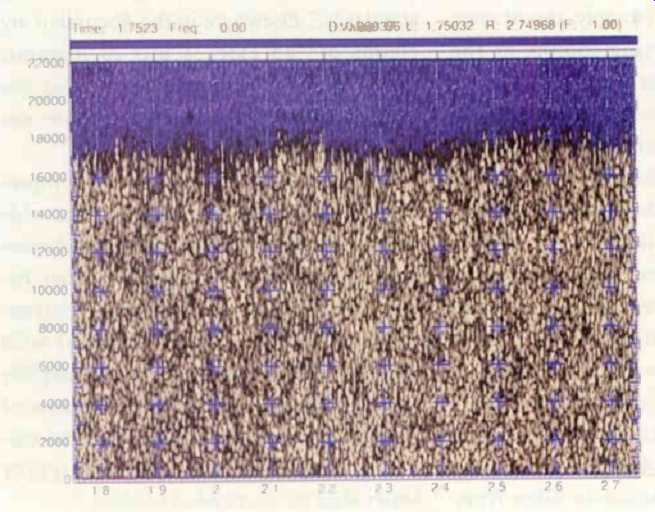
Fig. 4--Spectrogram of the Apogee UV-1000's noise floor. Visible in the band
at the top are multiple frequency modulations that, over time, tend to center
at the spectral peaks of Fig. 3 but vary as much as 1 kHz in either direction.
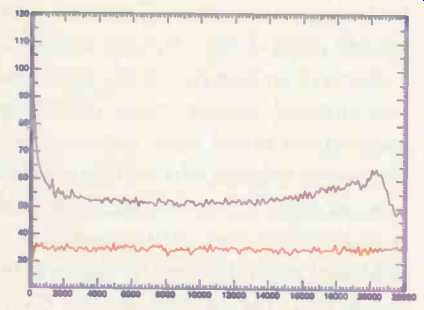
Fig. 5-Spectrum of the noise floor at the beginning of cut 6 on the first
Reference Recordings HDCD sampler (purple curve). Shown for comparison is the
noise spectrum of a Meridian 618 in its "flat dither" mode, fed by
a Lexicon 20/20 20-bit A/D converter with no input signal (red curve).
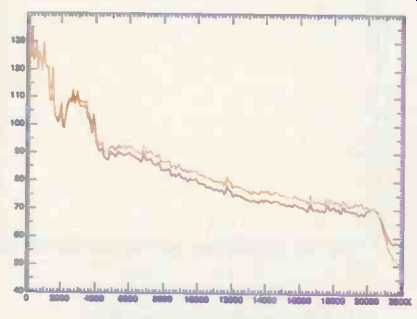
Fig. 6-Spectra of the opening 1.7 seconds from two versions of "Lux Aeterna" on
the second Reference Recordings HDCD sampler. The purple curve is for the HDCD
version, the orange curve for a version recorded through a conventional Sony
1630 16-bit A/D converter. Note the slight high frequency rolloff in the HDCD
spectrum, starting a little below 2 kHz.
The Apogee's noise floor itself, when digitally multiplied 60 dB, had the least unpleasant sound of any of the processors examined. The 4- to 5-dB reduction in noise below flat dither was readily apparent, and the signal was devoid of the strong "hissy" quality of flat dither. Notably absent were the crackling and frying sounds or the strangely hollow noises produced by some noise shapers. If a noise floor is to be heard, the Apogee's seems the most benign.
The Apogee is notable for what it does not do to music signals. There was no detectable alteration of the piano's timbre or its attack transients. No "hardening" of reverberation was perceived, nor was any stereo image alteration detected. In sum, the Apogee UV-1000 seems to go about its word-length reduction chores in a minimally intrusive manner. As with the other processes, however, caution is urged in generalizing these observations to other types of program material and other recording techniques.
HDCD Unplugged
Apogee's UV-22 is a low-profile process. Although there is a UV-22 logotype, it is rarely, if ever, seen on CDs, and few people outside the trade seem to know of its existence. Precisely the opposite is true of Pacific Microsonics' HDCD, or High Definition Compatible Digital, process. Prestigious publications such as The Economist ("un cannily realistic"), Fortune ("captures important aural cues"), and The New York Times ("fully flowered music") have covered HDCD. Specific information about how the process works is in short supply, but a document filed by Pacific Microsonics and published under the Patent Cooperation Treaty gives some insight into HDCD.
The system's principal benefits are claimed to be "ultra-low distortion" and "improved apparent resolution" while maintaining compatibility with standard CD players.
"The overall system of the invention," states the international application, "makes possible a more accurate reconstruction of the original analog signal than would have been possible using the same digital recording standards." Elsewhere in the document are claims of "an extra 4 bits of dynamic range" and "better spatial sense and less brittleness" as well as improved "inner de tail perception." The "smart optimization" techniques used in HDCD are also claimed to provide "improved sonics for portable and automotive playback when not decoded." That, Pacific Microsonics says, is because "conventional decoding. . .yields a signal with slightly less dynamic range and only slightly higher background noise." But, because of "lower quantization and slew induced distortions," the music will "sound equal to or better than an un-encoded product." Elsewhere in the patent document it is claimed that "signals lacking the encoding process [that is, conventional CDs] are provided some overall enhancement." In sum, according to these claims, everybody wins, and more than compatibility is provided.
Play an HDCD disc in your car, and it will sound better. Play a conventional CD through an HDCD decoder, and it will be better too. But best of all is supposed to be the combination of HDCD encode and de code, with its promise of "increased apparent bandwidth and resolution" and an implied 19- or 20-bit dynamic range.
To summarize the dense aggregate of techno-speak and legalese in the 88 pages of the international patent document, which includes 107 specific claims, it appears that there are a number of methods by which HDCD may operate on an incoming music signal.
The first of these is boosting low-level signals and attenuating peaks. This compress-during-recording, expand-during-playback function of HDCD appears conceptually similar to conventional compander-based analog schemes (such as Dolby and dbx noise reduction), but it is also stated that the process reduces distortion.
Amplification of low-level signals during HDCD encoding is claimed to "maintain a minimum LSB [least-significant bit] dither-like activity" that reduces distortion.
It is also asserted that the higher average recording levels permitted by peak compression further reduce distortion, albeit at the cost of increased distortion on "infrequent" peaks. Whereas conventional noise reduction usually relies on fixed and known signal levels for both the encode and decode operations, HDCD tells the decoder how to vary its gain via a code embedded in the least-significant bit as a part of a pseudo random dither noise. The gain increase on low-level signals helps conceal the code insertions, which for classical music are said to last for about 1 millisecond and occur several times per second "at most." It seems that the codes can, at least potentially, control at least two other HDCD functions. One of these is filter shape during playback. The document lists three types of interpolation filters-one for high level signals, another for low-level signals, and a third for transients. The HDCD de coder, if this function is implemented, switches between filter types according to signals in the control code. Pacific Microsonics claims that this technique re moves the need to "compromise" filter de sign and that both "extended high-frequency response" and "improved transient settling" are obtained.
A third potential operation of HDCD is "wave synthesis." When the HDCD encode processor detects a waveform with distortions "known to occur at the reproducer," another waveform can be substituted. The new waveform is either looked up in memory, amplitude scaled, and then substituted, or, alternatively, data is sent via the control subchannel to enable the HDCD decoder to synthesize the signal. The "restructured" waveform is said to have more data points and therefore reduced distortion. Pacific Microsonics says the wave-synthesis feature is not used now, however, as it was found to be unnecessary.
It is clear that HDCD potentially involves very large amounts of signal processing. Most of this appears to occur during en coding. The encoder incorporates an A/D converter running at an 88.2-kHz sampling rate and generating 24-bit words, 20 bits of which are devoted to the audio signal. Its output feeds a buffer memory that stores the signal while the encoding logic analyzes for its salient characteristics. Another system performs the actual HDCD operations, such as compression, and then generates the control codes that are embedded in the output signal.
At the receive end, a Pacific Microsonics LSI chip, which includes a digital interpolation filter along with the decoder, performs the "conjugate" operations, thereby producing a signal incorporating whatever improvement the entire process provides. In dependent of its HDCD decoding capabilities, the Pacific Microsonics PMD-100 chip is considered by some to be a very good filter that is adaptable to many D/A converter designs, and it is now used in equipment from roughly three dozen manufacturers. Those desiring HDCD should budget a substantial sum, as the average retail price of 42 D/A converters using the HDCD chip is now about $3,200, with a high of $15,950 and a low of $599. An out board converter is almost a necessity, as only six integrated HDCD players-with an average price of more than $2,700 and none below $1,995-were available in late 1995.
Beyond the cost issue is the fact that HDCD-encoded program material is still scarce. That is at least partly because there was no commercially available version of the HDCD encoder until recently. Consequently, most HDCD recordings have come from the San Francisco-based Reference Recordings label, with which Keith Johnson, one of the HDCD developers, has long been associated.
Reference Recordings has released two HDCD samplers containing examples of recordings made in the format. Since al most all of that material was originally captured on an analog tape deck without noise reduction, the recordings themselves tend to be somewhat noisy. This is seen in Fig. 5, which shows the quiescent noise floor for about a quarter of a second at the beginning of cut 6 on the first Reference Recordings HDCD sampler (RR-S3CD), Mike Garson's version of Miles Davis's "All Blues" (purple curve). The plot was made directly from the digital signal on the CD, ported into a Silicon Graphics computer workstation. Shown for comparison is the noise spectrum from a Lexicon 20/20 A/D converter feeding a Meridian 618 processor, presented in last month's measurements, with the 618 set to "flat dither" (red curve).
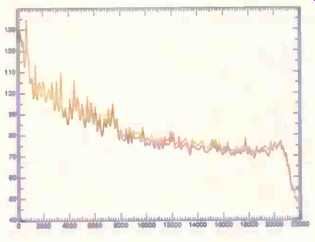
Fig. 7--Spectra from alternative masterings of "Moonglow" on the
second Reference Recordings HDCD sampler. As in Fig. 6, the HDCD version (purple
curve) rolls off slightly above about 2 kHz relative to the Sony 1630 version
(orange curve).
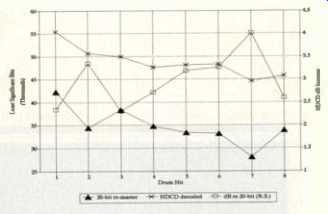
Fig. 8--Peak levels, in LSBs (left scale), of eight drum hits from two masterings
of Jimi Hendrix's "Gypsy Eyes," one a conventional 20-to-16-bit remastering,
the other an HDCD remastering. A third curve plots the energy difference between
the two, in decibels (right scale).
In the region of greatest aural sensitivity, roughly from 3 to 5 kHz, the noise in the Garson recording is 17 to 18 dB above the noise floor of the Lexicon/Meridian combi nation. That's equivalent to about 3 bits of resolution. Had the original recording been made digitally, roughly similar noise levels would have been produced by a 13-bit analog-to-digital converter.
Also seen in Fig. 5 is HDCD's use of dither, possibly of a high-pass form but definitely noise. The dither accounts for the rise in the noise floor beginning at about 13 kHz. Since Pacific Microsonics claims in its patent papers that dither "creates new distortion," its presence on these and other HDCD recordings is as interesting as it is enigmatic. This, however, is only the first of a number of surprising behaviors by the HDCD process.
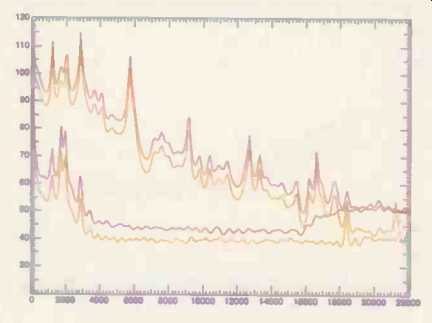
Fig. 9--Spectra for the "heads" (upper pair of curves) and "tails" (lower
pair) of a high-treble piano note. The purple curves are for the HDCD-encoded
version, the orange curves for an unprocessed 16-bit recording of the same
event.
Notwithstanding the relatively high noise levels and the very strange shift in piano perspective that occurs in the first part of the recording, the Garson "All Blues" is a sonic confection with plump but not over bearing bass, well-delineated brushwork, and a large (though still crisp) saxophone sound. If there is a "process" at work here, it is difficult to detect it.
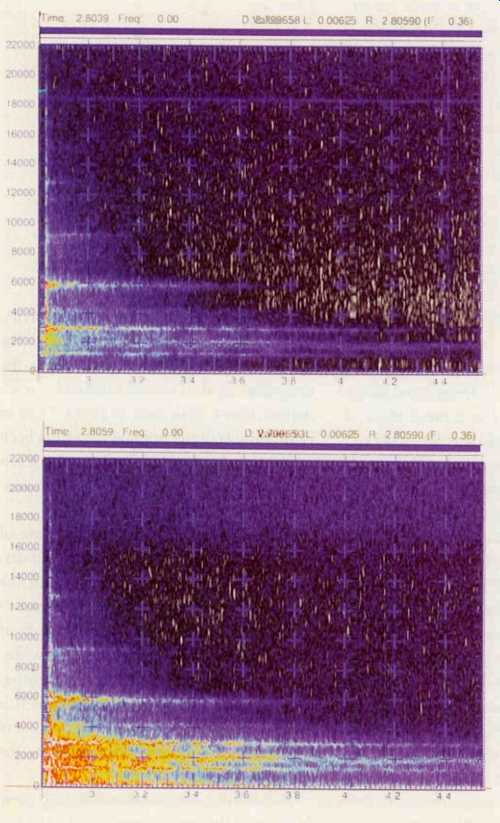
Fig. 10--"Three dimensional" spectrogram of the unprocessed 16-bit
recording of the entire piano note depicted in Fig. 9.
Fig. 11--Spectrogram of the HDCD-encoded rendering of the piano note. Note how the tails of the partials are lengthened and intensified.
A word is in order about the influence of D/A converters on this recording. The reference converter-an Apogee DA-1000 that is widely used in professional recording, mastering, and some instrumentation applications-has no HDCD-decoding capability. It produced a particularly pleasing rendition of the Garson. When played through two different HDCD-capable converters, one from Proceed and another from FAD, and with sound-pressure levels adjusted for equality in the opening bars, the presentation turned out to be audibly different.
In comparison with the Apogee, both HDCD-equipped converters sounded rolled off in the high treble-particularly evident in percussion-and, at the same time, the Garson recording took on a "wetter," more reverberant quality, as if the walls of the space in which it was recorded were moved back and the microphones placed further from the musicians. It is a personal matter as to which presentation is preferred, but the difference is distinct.
In a separate test I found that this difference was due in part to the characteristics of the PMD-100 chip, not as a decoder but as an interpolation filter. Through the courtesy of Madrigal Audio Laboratories, a demonstration was mounted in which the same Mark Levinson No. 30.5 D/A converter was alternately fitted with an NPC filter chip and the PMD-100. With conventional recordings and precise level matching, the PMD-100 exhibited a different high-treble characteristic. Whereas the NPC filter had a certain "glisten" or "edge" when presenting choral voices and strings, this effect was absent when the Pacific Microsonics chip was installed. In comparing the Apogee to either of the HDCD-equipped D/A converters, playing conventional recordings, the alteration of treble was more pronounced and was particularly apparent on the ride-cymbal figures common in jazz recordings. Potential adopters of the HDCD technology, particularly those with single-box CD players that are sometimes "bright," should carefully audition HDCD decoders to as certain that their performance on conventional recordings suits their taste and system characteristics. The HDCD-capable converters I auditioned have, to my ears, an inclination toward the mellow.
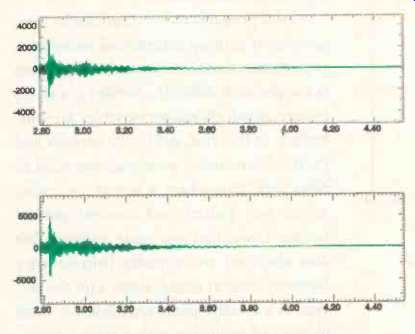
Fig. 12--Energy-versus-time plot of the unprocessed 16-bit recording of the
piano note, as depicted in Figs. 9 and 10.
Fig. 13--Energy-versus-time plot of the HDCD-encoded recording of the piano note, as depicted in Figs. 9 and 11.
Given the current paucity of HDCD titles (and even if HDCD is wildly successful, encoded discs will be a small fraction of the total catalog for many years to come), the issue of the rendering of conventional recordings is certainly pertinent and largely a matter of personal taste. With regard to HDCD itself, the issue is more clearly one of performance. The record there might be described as mixed, all puns intended.
A second Reference Recordings sampler (RR-905CD) contains HDCD versions and conventional Sony 1630 masterings of the same performances. I examined two of these, again by the all-digital method. The spectrum of the opening 1.7 seconds of "Lux Aeterna," a choral work from tracks 12 and 13, is seen in Fig. 6. In this section, peak levels nearly match, with the Sony 1630 version (orange curve) having a slightly higher peak level (+0.24 dB), measured in LSBs. Observe that at 1 kHz, the energy in the two versions closely matches, but as the frequency rises, the curves di verge. By 9 kHz the HDCD version is 3 dB down relative to the Sony 1630 version.
That difference is maintained to about 18 kHz, where the HDCD curve starts to rise slightly; by 21 kHz it is up 1.7 dB relative to the 1630 curve. This rise at near-ultrasonic frequencies is probably due to dither noise.
Except for that rise, the signal spectrum of the HDCD version of "Lux Aeterna" appears to have a substantial rolloff that be gins before 2 kHz (roughly three octaves above middle C) and continues far into the range of musical partials. Comparative listening with both HDCD and conventional converters, as well as with two single-box CD players, demonstrated that the spectral difference was readily apparent in all cases.
On another pair of tracks from the Reference Recordings sampler, alternative masterings of "Moonglow," the HDCD version's peak level measures 0.4 dB higher at the piano/percussion "hit" that begins the track. I also found a rolloff similar, but not identical, to the one on the "Lux Aeterna" cut, as seen in Fig. 7. At 2 kHz, the energy in the HDCD version is 0.1 dB below that in the Sony 1630 version, descending to-2.6 dB at 6 kHz. After rising slightly, about 0.3 dB on average, the HDCD signal is again down 2.5 dB at 13 kHz. As in the case of "Lux Aeterna," there is a sharp rise at extremely high frequencies.
Once again, the difference in the spectra of the two versions was easy to hear through a variety of converters. Among the discernible effects of the HDCD process was an alteration in the timbre of the trumpet solo and a shift in the position of the piano. Apparent reverberation grew greatly, and the position of the trumpeter moved back with respect to the rest of the ensemble. These effects were audible in both conventional and decoded playback. A general and further darkening of the sound field occurred when the recording was played back through an HDCD converter on four otherwise entirely different systems.
In a demonstration conducted by Pacific Microsonics with the "Moonglow" tracks, a distinctly concave sound field was created by the HDCD version: The horn ensemble was forward and roughly at the longitudinal axis of the speakers, while the trumpeter seemed far to the back. The Sony 1630 version did not exhibit this "warpage." Al though an interesting presentation, the HDCD "Moonglow" violates convention, which usually has the soloist in front. The measurable reduction in treble energy on this recording is probably the prime cause of the imaging changes relative to the standard track.
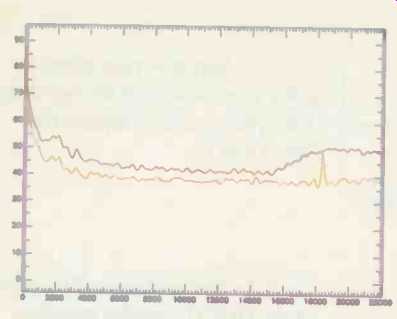
Fig. 14--Noise floors of HDCD-encoded and unprocessed 16-bit recordings (purple
and orange curves, respectively).
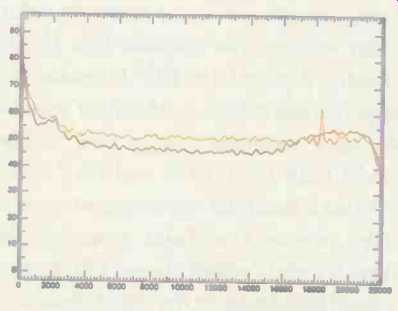
Fig. 15-Noisefloors of decoded HDCD and unprocessed 16-bit recordings (purple
and orange curves, respectively).
Another HDCD comparison is possible between a European HDCD release of Jimi Hendrix's The Ultimate Experience (Polydor 517 235) and a conventional, 20-bit-mastered domestic version (MCA MCAD-10829). Detailed analysis is confounded by both a speed difference (the HDCD being slower) and a polarity inversion. In comparison to a third, older version, The Essential Jimi Hendrix (Reprise 9 26035), the HDCD release again appears inverted but is of similar speed on the track examined, "Gypsy Eyes." Subjectively, both the HDCD and the "20-bit" CDs are substantial improvements over the older release. The reason is unclear, but there is a slight rolloff above 12 kHz, as well a small bass boost, in the oldest version.
Right from the start, the HDCD rendering of "Gypsy Eyes" delivers a subjectively startling presentation of Hendrix, whether decoded or not. One reason is found in Fig. 8, which shows the peak levels, in LSBs, for the first eight drum figures (a bass drum and hi-hat combination in which the bass drum naturally dominates the peak measurement). The data was taken from the balanced analog outputs of an HDCD-capable Proceed Digital Audio Processor (D/A converter), converted again from analog to digital by an Apogee AD-1000 running in 16-bit mode and transferred to the computer. There were substantial differences in both peak and relative levels.
On the first beat (reading the difference curve against the right-hand scale of Fig. 8), the HDCD version is 2.3 dB higher than the 20-bit-mastered version. This difference grows to 3.3 dB on the second beat, drops by about I dB, and then climbs to a 4-dB differential by the seventh event. The eighth "hit" drops back to a 2.6-dB advantage for HDCD. The increased level is probably one reason for the subjective power of the HDCD version of this track. Since the relative level keeps changing, it is impossible to make a level-matched comparison.
If one thinks of the shapes of the 20-bit-mastered and HDCD curves (which read to the left-hand scale in Fig. 8) as musical indicators, it is clear that there is a rhythmic difference between the two versions. This is most apparent at the second and seventh events, but the overall shape of the curves is also different. As to which of these is "correct," the answer is unknowable: Both may have been subjected to other processes. It seems, however, that in the HDCD mastering the engineer may have taken advantage of the "gain interplay" features of HDCD, in effect using it creatively. The "oldest" version of "Gypsy Eyes" (not shown) yielded yet a third set of levels. The philosophically or musicologically inclined may wish to ponder the question: What did drummer Mitch Mitchell really play?
The Ultimate Comparison
As you probably have recognized by now, analysis of existing commercial recordings, even those released for formal comparison, is fraught with difficulty. Needed is a stable process in which known variables are controlled. To that end, an HDCD encoder and Pacific Microsonics personnel ventured to New York City, where a superb recording venue was rented and concert pianist Jerome Lowenthal was again engaged. We also obtained an exquisite 19th-century Steinway concert grand, along with the ser vices of a concert-piano technician. A small platoon of engineers with a large complement of equipment was in attendance, along with me and both the Editor and Publisher of Audio.
The purpose of the exercise was to obtain directly comparable master recordings, all fed simultaneously by the same micro phones and microphone preamplifier. Master media comprised a Nagra 20-bit digital recorder, an HDCD encoder feeding a 16-bit Sony DAT machine, a Stellavox professional 16-bit DAT deck, and two analog recorders, one a Studer 1-inch transport with custom tube electronics designed by Tim de Paravicini and the other a standard Studer quarter-inch, solid-state model. (A CD containing all versions of this comparison recording will be offered to Audio readers in the near future for evaluation on their own systems.) I later made measurements comparing the digital information in the HDCD-en coded and 16-bit Stellavox recordings.
(This was straightforward and avoided any need to process a 20-bit recording.) In listening to the two recordings, I noted the most marked differences at relatively low levels, particularly when using the Apogee D/A converter. With respect to the Stellavox DAT, the HDCD rendering of passages in the region of -20 dBFS was noticeably "wetter," and both the sustain of the piano and its timbre were altered. The first impression was similar to that created by the "rolled-off" HDCD tracks on the Reference Recordings samplers, particularly with respect to the sense of greater reverberation.
In this case, however, no high-frequency rolloff was apparent, as short-interval measurements of the signals yielded essentially similar spectra on typical events when adjusted for level.
Refer to Fig. 9 for the likely solution to the mystery. The upper pair of curves shows the spectrum of the HDCD rendering of the "heads" of two high treble notes (purple curve) and just below it the DAT rendering (orange curve). This event is "out in the open" and sustains for about 1.75 seconds.
At all of the many points measured, there is a 5-dB differential, ±0.1 dB, which is reasonably linear for the comparative deviations of two separately recorded signals.
Now examine the lower pair of curves in Fig. 9, the spectra of the "tails" of the same event over a period of 330 milliseconds.
Here deviations at the peaks range from 9.5 dB at 1.25 kHz to 8.7 dB at 2.85 kHz. By 5.8 kHz the HDCD signal is into the noise floor, which is about 5 dB above the DAT noise floor until the HDCD dither starts pushing it further up at about 16 kHz. (The 6-dB spike in that DAT signal at 18.3 kHz is a recording artifact rather than part of the signal.) What this indicates is that HDCD raises the tails of musical events dynamically and probably introduces a time-varying frequency and amplitude response. Implied by this behavior is the ability to distinguish signal from noise, which might possibly be done by autocorrelation. In any case, this example shows that HDCD encoding materially alters signal dynamics in audible ways. Listeners are invited to decide for themselves if this is an acceptable trade-off for the claimed HDCD benefits.
Figures 10 and 11 are full "three-dimensional" (time, frequency, and amplitude) spectrograms of the straight 16-bit DAT and HDCD versions of the entire event. You can see the tendency of HDCD to lengthen and strengthen the tails of the partials. The partial at 5.8 kHz, for example, is about a quarter of a second longer in the HDCD recording than in the unencoded DAT recording. Substantial increases in the low level partials are also evident; locally, these variations can exceed 10 dB between the two signals.
The energy-versus-time plots (all frequencies summed) corresponding to Figs. 10 and 11 are shown in Figs. 12 and 13. Interestingly, there is little difference except in the tails. Without knowing the behavior of HDCD, one might attribute the fattened tail on the plot to the roughly 5-dB difference in large-signal amplitude.
Decoding does improve HDCD's behavior. The curves in Fig. 14 show the relative quiescent noise performance of undecoded HDCD and the straight 16-bit recording. In this condition, HDCD's measured noise is clearly higher (typically between 5.7 and 4.5 dB from 3 to 5 kHz and dropping slightly, to between 4 and 5 dB, from 7 to 15 kHz, after which the floor rises because of HDCD's dither). But since HDCD's companding action raises the recorded level by about 5 dB at low to moderate inputs (-20 dBFS or be low), an undecoded HDCD disc can still have a signal-to-noise ratio roughly equivalent to that of the conventional 16-bit recording.
The curves in Fig. 15 indicate the comparative noise levels for the same recordings but with the HDCD segment decoded. This data was captured by taking the balanced analog output of the Proceed D/A converter and taking it back to digital with an Apogee AD-1000 A/D converter operating at 16 bits. (To keep the Apogee converter's own noise from confusing the measurement, I used its gain controls to raise the input level about 13.5 dB.) The curves show the quiescent noise of decoded HDCD is below that of the straight 16-bit recording, which suggests that the process is providing some noise-reduction effect. But whereas the undecoded HDCD signal was 5 dB above the straight 16-bit level, the decoded HDCD signal is 1 dB below the 16-bit when measured at the same point. Although the signal level swings 6 dB between the two for mats, the noise level drops somewhat less.
At 4 kHz the noise of HDCD is about 4 dB lower than the straight 16-bit; at 5 kHz this difference grows to 5 dB in favor of HDCD and then drops to about 4 dB until 11 kHz, where it again approaches 5 dB. Even given potential differences introduced by the de code to analog and return to digital, it does not appear that HDCD provides a large noise advantage over conventional 16-bit recording on this program material, even with an exceptionally quiet source such as that provided for the test recordings.
The significance of that fact becomes evident when you consider that the test recordings are substantially quieter than any material yet released in HDCD. This implies that HDCD is not getting much closer to true 18- or 19-bit equivalent performance than the noise shapers. At least in part, that is because HDCD is no more able than other processes to overcome the limitations of hall, microphone, and micro phone preamplifier noise.
The Bottom Line
It is clear that HDCD encoding audibly changes the spectra and envelopes of piano tones. Decoding the signal largely eliminates this problem, however, which is to say that the levels within spectral peaks on the heads and tails of notes are the same (with in about 0.5 dB) in decoded HDCD recordings and conventional digital recordings of the same passages. Examination of the spectrograms for the two signals also reveals much greater similarity after decoding of the HDCD version. (These spectrograms are not shown because the differences are so small that they would probably be obliterated in reproduction.) Decoded or undecoded, HDCD has a signature sound, some portion of which is attributable to the encoding process, the rest to the decode side and, particularly, to the sound of the digital filter incorporated in the HDCD chip. Perhaps this characteristic follows from a certain reverence for analog on the part of HDCD's designers. Of all the processes examined, HDCD is the most aggressive and obvious in operating on the incoming signal. Pacific Microsonics undoubtedly would say that such operations are necessary to overcome the limitations of the digital medium. There is no clear evidence to support such a claim, however, at least in the test recordings or other material currently available, and the nature of the process raises other issues.
In particular, there is the matter of undecoded playback. The way in which HDCD operates on a piano signal has strong musical implications. The rate of sustain, which is altered by HDCD in the example presented, has been the subject of intense development by piano makers for two centuries or more. The "singing" quality for which some pianos are renowned emerges during sustain, and artists modify sustain through subtle manipulations of the piano's pedals.
Measurable modification of sustain, what ever its motive, is not likely to yield a faithful reproduction of either the instrument or its use by artists who create refined performances in any genre.
The effect seen and heard on the grand piano is probably not confined to it. Any instrument that continues to sound after it is struck-be it a plucked string on a violin or guitar, a drum, a cymbal, or a vibraphone has a characteristic decay that is probably susceptible to modification by HDCD.
When altering such signals, the process also modifies the associated reverberation. That may possibly account for at least some of the tendency for HDCD recordings to sound "wetter" than conventional recordings. For those who prefer a recording style built around large spaces and a relatively distant perspective or who believe analog recordings are somehow "richer" than digital recordings, HDCD may well be deemed an aural success. If, however, the criterion is accurate reproduction of a musical event, then HDCD's signal-processing operations are less successful, particularly when they're not decoded.
Most remarkable, though, are the wide spectral variations evident among various recordings that are all claimed to represent "good" sound. The 15-kHz energy found in the cymbals on the Super Bit Mapped Sony Mastersound Kind of Blue and the HDCD version of "Moonglow" might easily differ by 15 dB or more. Digital technology is clearly being used to serve greatly varying aesthetic objectives and preferences. And if SBM and HDCD represent the future, or perhaps alternative futures, the traditional canons of recording and high fidelity are in need of revision.
(adapted from Audio, Apr. 1996)
Also see:
19 Bits in a 16-bit Sack (Mar. 1996)
The Promise & Problems of Computer Sound Boards (Nov. 1995)
Computing audio's future (Jan. 1994)
The Trouble with Jitter (Jan. 1996)
= = = =