by D. W. Fostle
[D.W. Fostle is the author of The Steinway Saga (Scribner, 1995), an account of the piano-making family and their instruments. His techniques for computer-based measurement of musical signals, developed in researching that book, form the basis of this article. The author wishes to thank Silicon Graphics and Entropic Research Laboratory for systems and software support.]
Noise shaping is today's hot CD mastering technology so what is it, and does it really make a difference?

===========
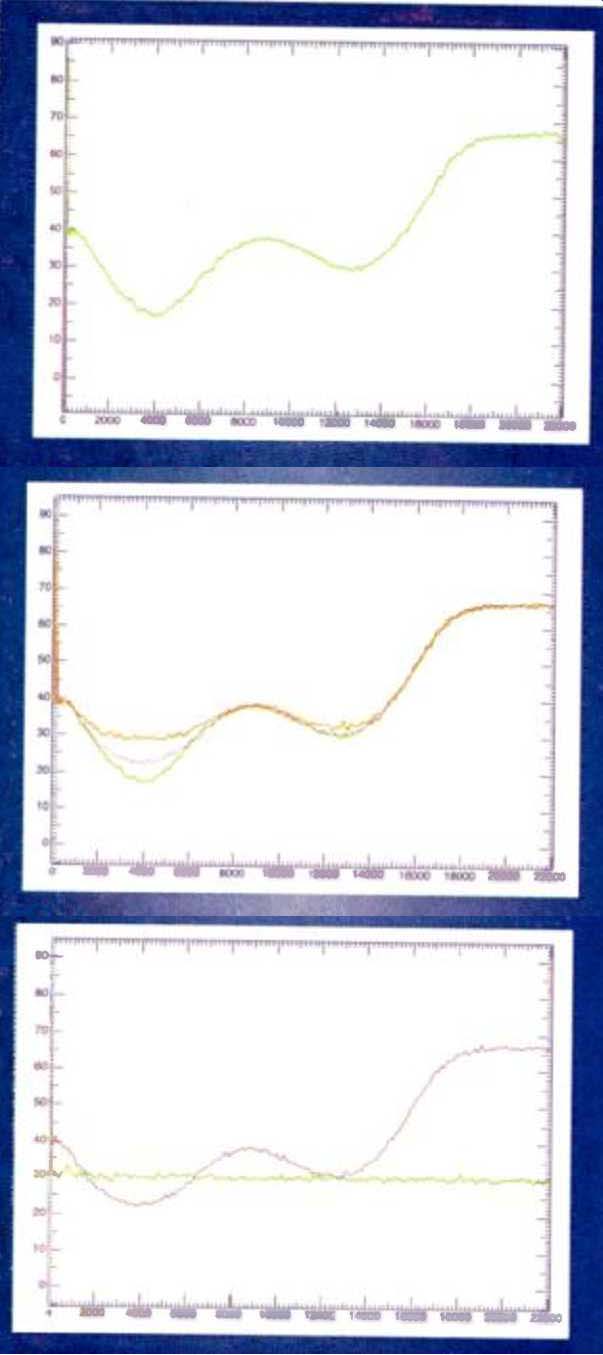
Fig. 1--The Weiss SFC-1's noise-shaping spectrum. Note the pronounced dip in the noise floor around 4 kHz, where the ear is most sensitive, and the steep rise at very high frequencies, where it is least sensitive Decibel scales here and on most following graphs show relative, not absolute, levels.
Fig. 2--The Weiss SFC- l's shaped 16-bit output-noise spectrum with no input (green curve) and when fed by two popular 20-bit A/D converters, the Lexicon 20/20 (purple curve) and the Wadia Digital 4000 (red curve), with no audio input. The converters' noise partially fills in the dips in the SFC-1 's noise floor.
Fig. 3--The Lexicon 20/20 A/D converter's noise floor (green curve) and the noise-shaped 16-bit output of the Weiss SFC-1 fed from the Lexicon with no input signal (purple curve).
===========
A formerly exotic engineering technique called noise shaping has entered the audio mainstream. Chances are you own CDs bearing the logos of some of the proprietary noise-shaping systems developed by major labels to transfer their 20-bit master tapes to the 10-bit CD format with minimum audible degradation. Sony's Super Bit Map ping (SBM) and Deutsche Grammophon's Authentic Bit imaging (ABI) are among the digital procedures that promise greater transparency, unproved resolution, and reduced noise in what some have called "10-bit-equivalent" recordings.
The practice of transferring old analog masters to 20-bit digital format and then noise-shaping the copies for rerelease on CD is also growing. Available now are the legendary Impulse "Blues and the Abstract Truth" sessions by Rudy Van Gelder and the renowned Everest "mag-film" classical recordings engineered by Bert Whyte. Sony has been a leader in rereleasing the works of some of the major names in pop and jazz:
Boston, Dave Brubeck, Miles Davis, Bob Dylan, Robert Johnson, Pink Floyd, and Weather Report, among many others, are available in the company's premium Mastersound series, all with SBM processing.
There is also a considerable amount of stealth noise shaping on recordings that carry no identifying logo or label note. A recording by a famous "grunge" band shows treble lift in the noise floor for a few milliseconds before the onset of modulation; this is noise shaping's "smoking gun," but visible only by spectral analysis. Those whose CD collections are flannel-free zones and whose tastes incline to recondite pro grams on the audiophile labels may be surprised to learn that these types of recordings, too, are sometimes noise-shaped without notice.

Finding the Noise Floor
Noise shaping for CD mastering grew out of the appearance of so-called "20-bit" analog-to-digital (A/D) converters in the early 1990s. A method was needed to properly shorten the word length of the converters to the 16-bit format of the Compact Disc.
As an alternative to simply chopping off, or truncating, the extra bits, as was some times done, or (better) rounding off and redithering, members of the Audio Research Group at Canada's Waterloo University proposed a means to retain some of the benefits of the theoretically lower noise levels on the 20-bit masters.
On paper, a full-scale 20-bit digital representation of an analog signal can resolve more than 1 million discrete levels (220, or 1,048,576, to be exact), whereas a 16-bit representation of the same signal has a potential resolution of just 65,536 levels (2^16).
The difference between the actual level of a signal sample and the nearest discrete quantization level that it can be assigned by the A/D converter is known as the quantization error, which manifests itself during playback as noise and distortion. The longer the word length, the finer the level gradation available to the converter, which in turn reduces quantization error and, thereby, noise and distortion. For true 20-bit conversion, the theoretical level of quantization noise and distortion works out to -122 dB relative to full scale (maxi mum level, or 0 dB), as compared with -98 dB for a 16-bit converter.
These engineering measurements do not make intuitively sensible the magnitude of the quantities involved. A $10,000 stock market investment that rose 98 dB would have a value of about $794 million. If that sum represented a "16-bit portfolio," a 20-bit portfolio would be worth $12.7 billion.
Saying that one 3-foot pace represents the theoretical noise in a "20-bit full-scale walk" implies a hike of almost 722 miles; for a 16-bit walk, the distance shrinks to 45 miles.
So impressive ratios lurk inside the deceptively unprepossessing quanta designated by 16 or 20 bits. If a way could be found to preserve some of the information in the 20-bit representation, that presumably would be a good thing. After all, it seems undesirable to turn that $12.7 billion port folio into one worth a mere $794 million.
Enter noise shaping, which is nothing more than a particular type of digital filter applied to a signal in a particular way. The goal of the filtering operation is to save some of that $12 billion we are about to throw away while creating the illusion that we have saved much of it. The basis for this clever trick is the long-known nonlinearity of human hearing, which is most sensitive in the region of 4 kHz. If you remember when hi-fi gear was equipped with "loudness controls" (which purportedly compensated for our reduced sensitivity to bass at low sound pressure levels), then you al ready know something about the phenomenon, which is based on our perception of equal loudness.
Curves of equal loudness versus frequency are determined empirically. Subjects are asked by experimenters to state when a tone or a narrow band of noise is equally loud in comparison to a reference tone or noise. By comparing the actual sound pressure levels that create the impression of equal loudness, you can plot the frequency response of the subject's hearing for a given reference level. As the level of the reference stimulus rises, these curves tend to flatten out (al though they never come anywhere close to being completely even). At low levels, doubling the frequency of a 4-kHz tone that is just audible may require boosting it by roughly 20 dB to keep it audible at 8 kHz. At low frequencies the nonlinearities are much larger: Dropping the 4-kHz tone to 40 Hz might require a 40-dB increase in sound pressure to create the impression of equal loudness. Variations from person to person can be very large, however, and standard deviations of 3 to 10 dB are reported. A range of ±3 standard deviations conventionally encompasses 99.7% of a population, so we might well expect individual judgments of equal loudness to diverge as much as 60 dB in extreme cases, depending on frequency and level. An equal-loudness curve derived from averaged responses may therefore be an inconsistent predictor of individual responses.

Noise shaping for CD mastering takes advantage of the treble portion of the ear's nonlinearity (loss of hearing sensitivity is actually more pronounced in the bass, but filters for the high-treble range require much less computing power). In the process of requantizing a (usually) 20-bit signal down to 16 bits, the shaping filter digs a depression in the 4-kHz region of the 16-bit noise floor, where we would be most likely to perceive it. The noise is not reduced in total; in fact, total noise power is s increased. The noise energy excavated in the 4-kHz region is piled up, so to speak, where it will be harder to hear, principally above 13 kHz. The original work on noise shaping set the filter contour to match the 15-phon ISO equal-loudness curve (i.e., the curve of levels needed to make each frequency equal in perceived loudness to a 1-kHz tone at 15 dB SPL).
==============
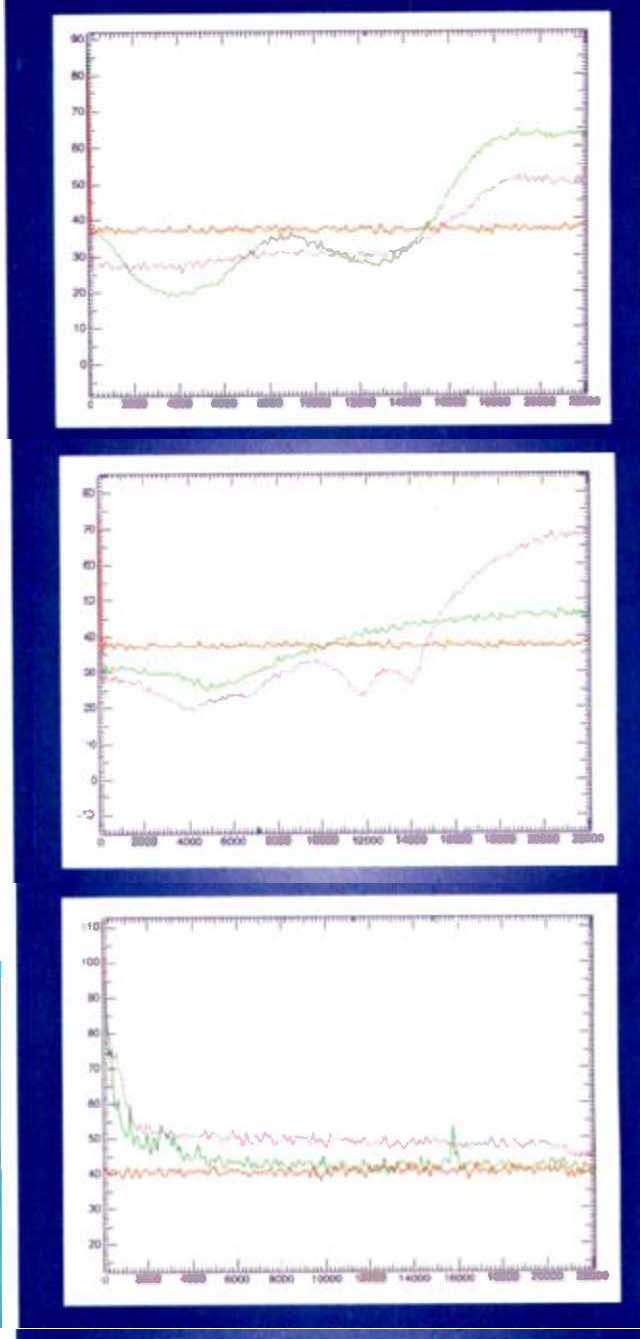
Fig.
4--Noise floors of Weiss SFC-1 noise shaper (green curve) and Sony's Super
Bit Mapping system (purple curve), fed by a Lexicon 20/20. The flat (red) curve
is unshaped 16-bit TPD (white-noise) dither from a Meridian 618.
Fig. 5--Output of Meridian 618, its most and least aggressive noise-shaping settings (purple and green curves, respectively) and at its flat-dither setting (red curie).
Fig. 6---Noise floors of two digital recordings from audiophile labels ( purple and green curves) and Gaussian noise at-% dBFS for reference (red curve).
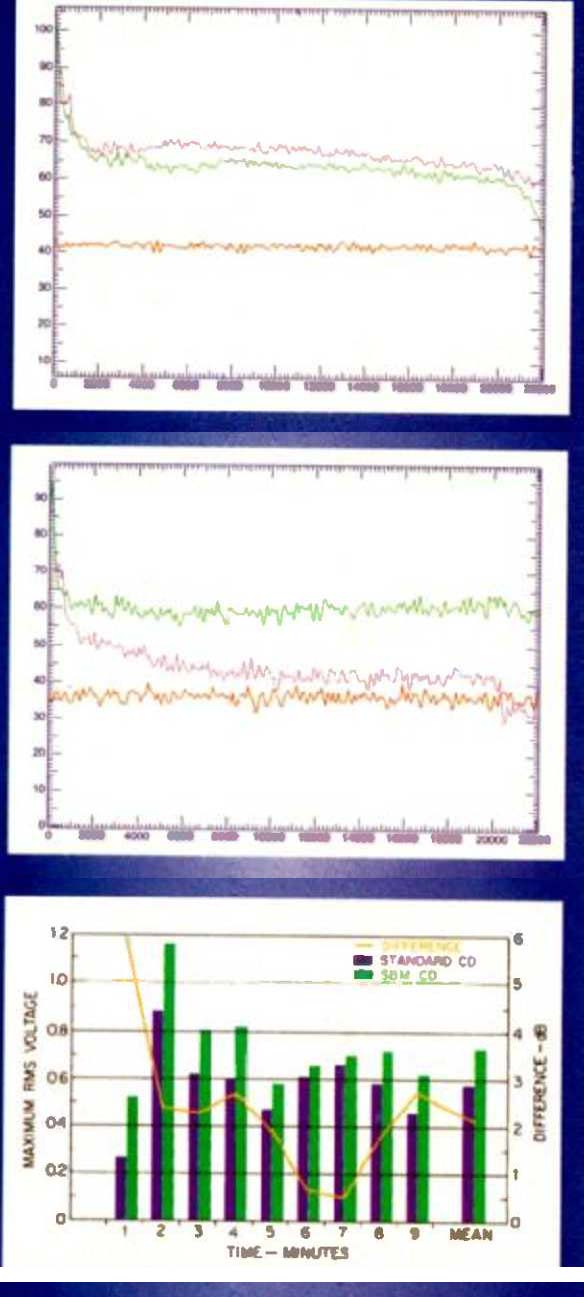
Fig.
7--Noise floors of an Aretha Franklin track from the 1960s (purple curve) and
of a cut from Cassandra Wilson's Blue Light 'Til Dawn CD of 1993 (green curve).
The flat reference is Gaussian noise at-% dBFS (red curve).
Fig. 8--Noise floors of the original CD release (purple curve) and SBM-processed Mastersound CD release (green curve) of Miles Davis '3 Kind of Blue. The flat (red) curve is Gaussian noise at-96 dBFS, about the lower limit for a 16-bit medium without noise shaping.
Fig. 9--Maximum level difference, minute by minute, in "So What" on the original and SBM-processed Mastersound CD releases of Kind of Blue.
===============
Noise shapers of the type used to convert 20-bit masters for I6-bit CDs work as follows: The bottom four bits are clipped from the 20-bit signal and fed back into the in coming signal through a filter that alters the spectral shape and adds dither. A delay is involved that is determined by the number of coefficients in the filter (digital filters work by multiplication of numbers). The University of Waterloo group proposed a filter shape based on the psychoacoustic data described above; it was not long, how ever, before claims were made that listening tests revealed other shapes to be sonically superior. Sony's SBM curve is one such alternative, and there are others.
Figure 1 shows the spectrum of a commercially available noise shaper, the Weiss Engineering SFC-1. Though not widely known among audiophiles, Weiss's superbly built equipment is used in hundreds of mastering rooms worldwide.
The Weiss curve is shown here because it represents a "pure" implementation of the original concept of equal-loudness-based noise shaping. Ignoring the spike below 50 Hz, which results from low-frequency noise, you can see that the curve descends to its minimum at 4 kHz, then rises about 21 dB at 9 kHz, dips back 8.4 dB to mimic the increased sensitivity of the ear in the region of 12.5 kHz, and then continues its ascent to about 18 kHz, where it levels off. Trough to peak, roughly 50 dB of shaping is applied to the noise floor. It is a curve of this type that is the basis for the "19-bit-equivalent" claims.
The quantization noise in a theoretical 19-bit channel is at-116 dB; in the region immediately around 4 kHz-and only that region-a noise shaper like the Weiss approximates that performance. At 2 and 6 kHz, for example, the noise is somewhat higher, roughly equal to that of a 17-bit channel. And, obviously, at very high frequencies the noise is much greater than in a pure 16-bit system.
There are other caveats as well. The use of a specific equal-loudness contour also implies a specific sound pressure level for the music above the shaped noise floor. At any other level, the shaping will not be optimal (though it may be very close), and some degradation of perceived noise performance must occur. Perhaps some people do listen to Hootie and The Blowfish, the Tokyo String Quartet, John Coltrane, and the Chicago Symphony at the same levels; others almost certainly do not. Further, hearing either the noise floor itself or a substantial portion of the musical information that is supposed to be preserved by noise shaping implies playback at very high levels. If we expect to hear the alleged "19-bit resolution" (assuming no masking by ambient noise in the listening room and the availability of a playback system that does not degrade the signal-to-noise ratio), we must achieve peak levels nearing the thresh old of pain. Systems capable of such performance are few and far between, so it is plausible that only a handful of people can benefit fully from 19-bit-equivalent noise levels-assuming they actually exist on some recordings.
If the noise floors produced by various shapers are digitally multiplied by 1,000 in effect, amplifying them by 60 dB-the sound that results is strange and markedly different by type. The sonic impression of the Weiss implementation might be de scribed as a hollow hiss, while the gain-multiplied floor of the Sony SBM shaper, though less hissy, contains a distinct crackle reminiscent of frying eggs. The most aggressive noise-shaping curve of the ones I have examined, the Meridian 618's Curve D, gives the impression of a very sharp fizz that is almost pitch-distinct. It is probably a good thing that we do not hear these noise floors under normal listening conditions.
Hitting the Wall
In practice (meaning, in real recordings), 19-bit performance is not achieved at any frequency and probably cannot be, given the current state of the art. Consider the curves of Fig. 2, which compares the spectrum of the Weiss SFC-1 under three conditions. The first condition, and the lowest (quietest) curve, is the output of the SFC-1 with no input. The next curve shows the SFC-1 fed by a popular 20-bit A/D converter, in this case the Lexicon 20/20, which has a specified 112-dB dynamic range. You can see that the noise level increases by 5.8 dB, or nearly 1 bit, at 4 kHz. The uppermost curve shows the noise floor of the SFC-1 when combined with another, somewhat noisier 20-bit converter having a claimed dynamic range of 108 dB, a Wadia Digital 4000. Another 6.3-dB increase in the 4-kHz noise level can be seen.
Figure 3 compares the Weiss's shaped output to the noise spectrum of the Lexicon converter itself, without shaping. At 4 kHz, the shaped noise is about 7.3 dB lower than the unshaped noise, and some advantage is apparent between 1.6 and 6.4 kHz. Al though a benefit is obtained, it is smaller than might be anticipated from the characteristics of the noise shaper alone. The original University of Waterloo research papers cautioned that the full benefits of noise shaping require very low-noise signals. In practical recording systems, such signals are rare, if they exist at all.
Some makers of professional A/D converters provide signal-to-noise specifications; others do not. When given, the noise ratings of 20-bit converters typically fall around-105 dB, only about 7 dB better than the theoretical noise floor for a full 16 bits. So while they can provide 20 bits of data from an audio input, true resolution is usually in the vicinity of 17 bits. To move the roughly 3 bits, or 18 dB, to full 20-bit performance implies a factor-of-eight reduction of noise. That is no small task, and if sonic nirvana is a million-to-one signal-to-noise ratio, nobody is going to get there soon.
Accepting that we're not likely to get all that noise shaping promises, how do some of the systems in use today stack up? Figure 4 compares the noise floors of the Weiss SFC-1, with its "pure" psychoacoustic approach, and the most famous noise shaper of all, Sony's Super Bit Mapping system, both fed by the Lexicon 20/20 A/D converter with no input signal. Based on its own re search, Sony seems to have abandoned any attempt to closely mimic an equal-loudness contour and opted for a broader, shallower depression in the noise floor. The SBM curve is roughly flat between 1 and 5 kHz.
By 7 kHz it is up 2 to 3 dB, where it remains until about 13 kHz, rising from there to a plateau around 18 kHz. Trough to peak, the SBM curve measures about 26.5 dB, or 20 dB less than the Weiss SFC- l under the same conditions.
The red curve in Fig. 4 is the spectrum of the Meridian 618 in its triangular-probability-distribution (TPD), or "flat," mode.
This is an unshaped white-noise dither that represents the minimum practical noise floor achievable with low distortion and without shaping when converting from 20 to 16 bits. With respect to the TPD line, SBM is about 9 dB quieter at 4 kHz, where as the SFC-1 achieves a 17-dB reduction at the same frequency. On the other hand, SBM excels below 2 kHz and from approximately 7 to 10 kHz, and it produces a smaller noise bulge at very high frequencies.

The Meridian is not limited to TPD dither, however. The user has a choice of curves ranging from flat to the most aggressive noise shaping I've examined, along with recommendations from Meridian on their use. For example, Meridian provides separate curves for optimizing loudspeaker and headphone listening, as well as facilities for pre-emphasis and digital gain change.
When connected to the same A/D converter as the Weiss and Sony noise shapers, the Meridian produced the curves shown in Fig. 5, achieving a maximum reduction from its own flat dither of 18.6 dB at 4.2 kHz and, for a much milder alternative shaper, 12.5 dB at 4.8 kHz. The Meridian's peak noise is about 30 dB above the flat dither. With its trough-to-peak range of 50 dB at its most aggressive setting, the Meridian displayed the greatest alteration of noise floor among the shapers tested when connected to an A/D converter.
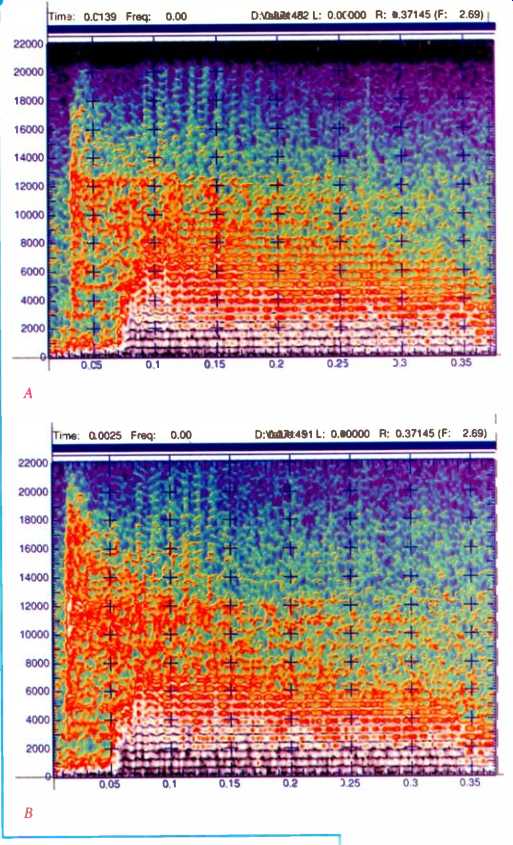
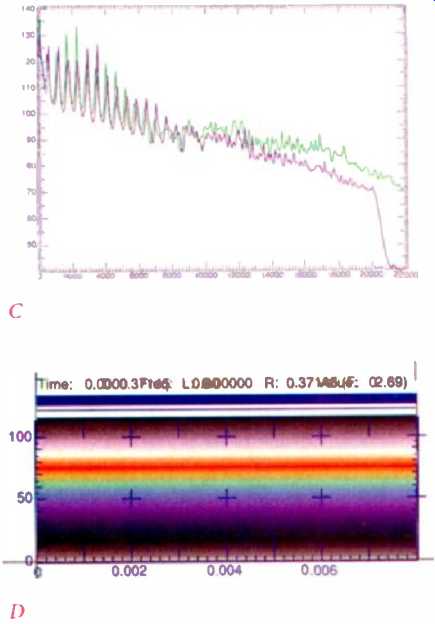
Fig.
10--Spectrograms of approximately 400 milliseconds from the original CD release
(A) and Mastersound CD release (B) of Kind of Blue. Time is shown horizontally
in seconds, frequency vertically in hertz. Amplitude is indicated by color.
Amplitude-versus-frequency plots (C) for the same interval show equalization
and bandwidth differences between the original version (purple curve) and SBM-processed
Mastersound version (green curve). Color key (D), shown at bottom, is for Figs.
10A, 10B, 11A, and 11B.
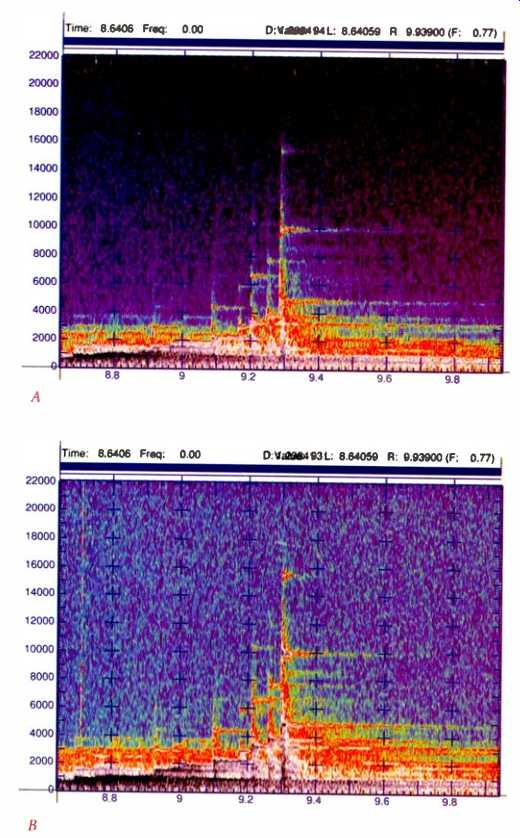
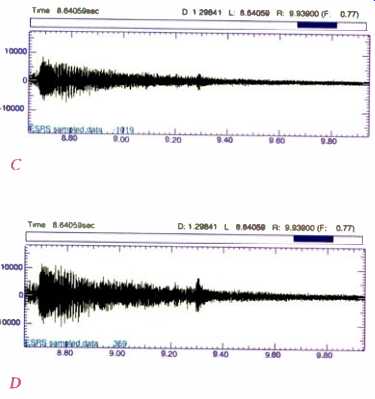
Fig. 11--Spectrograms of about 1.3 seconds from a high piano arpeggio near the start
of "Strange Meadow Lark" on the original (A) and Mastersound
(B) CD releases of Dave Brubeck's Time Out. Equalization of the Mastersound
version is even more evident here than on the Miles Davis. Amplitude-versus-time
plots for the old (C) and new (D) versions show the EQ's dramatic effects on
musical dynamics and phrasing.
So you can readily see that there are considerable differences among the various noise-shaping options available, even though all are said to be based on similar principles and directed to the same objective, a reduction in subjectively experienced noise. Moreover, each of the systems delivers less effect when connected to a real A/D converter than when operated alone.
What was first shown in the case of the Weiss SFC-1 is true for the others as well: The noise from the converter "fills in" the lowest portions of the shaped noise floor in much the same way that the lowest part of a basement is the first to fill with water in a flood. This phenomenon makes the noise shapers somewhat less effective than theory or stand-alone performance tests would suggest.
Unfortunately, the converter is only part of the story. We have yet to consider performance spaces, microphones, preamplifiers, mixing consoles, and so forth, all of which add further noise. Before getting into that, however, let's take a look at the noise levels on some real recordings, beginning with Fig. 6, which shows the noise floors of two digital recordings from audiophile-label sampler CDs. For reference (red curve), I synthesized Gaussian noise at an rms level of 96 dB below digital full scale. (I chose that level because it represents excellent performance for more than 30 actual "purist" recordings that I examined.) The quieter of the two recordings comes within about 3 dB of the-96 dB curve, while the noisier is about 9 dB above it. The spike at 15.7 kHz in the quieter curve is a common artifact, leakage into the audio channel of signals from computer or video monitors at the NTSC horizontal-scan frequency. The noise levels of some analog audiophile recordings released on CD can be as much as 12 to 13 dB higher still. Such productions may have noise performance roughly equivalent to that of a digital recording with a resolution of 12 or 13 bits.
Those who believe that the passage of time must bring technical progress will be disappointed by Fig. 7. It compares an Aretha Franklin track from the 1960s to a cut from the critically acclaimed Cassandra Wilson Blue Light 'Til Dawn CD (Blue Note 81357) of 1993. Despite the lapse of roughly a quarter-century between the two sessions, the noise floors are similar. At 4 kHz, the passage of time brings a 1.6-dB improvement, largely the result of equalization that pushes down the noise between 3.7 and 7.5 kHz on the Wilson disc. The EQ imparts an "inky" quality to the tracks that, given the music, somehow seems apt. By 5 kHz, Cassandra bests Aretha by about 6 dB, but the noise is still almost 22 dB (12.6 times) higher than the-96 dB reference curve. It is difficult to find enough silence on pop recordings to make this type of measurement, but two on which there is some, Nirvana's In Utero (Geffen DGCD 24607) and Sons of Soul by Tony! Toni! Tone! (Mercury Wing 514933), exhibit 4-kHz noise levels nearly 22 and 13 dB, respectively, above the-96 dB curve. From this it can be inferred that the Wilson noise levels are not unusual.
Perhaps the most important point is that typical listeners readily accept noise markedly higher than the theoretical 16-bit floor. This acceptance extends not only to popular recordings but also to some, probably most, analog audiophile recordings.
The Real World of Reissues
Easily the most amazing manifestation of noise tolerance, at least to me, is the pandemic critical approval of some releases in the Sony Mastersound series. Positioned as a demonstration of the sonic potential of "the revolutionary 20-bit Super Bit Map ping process," to quote from a brochure found in a record store, the rereleases in the Mastersound Legacy series are said to deliver "unprecedented clarity and accuracy."
Actual comparison of the near-silence in the first two seconds of "So What" from Miles Davis's seminal Kind of Blue in the standard (Columbia CK-40579) and Mastersound (CK-52861) releases can only be described as surprising. The initial probings of Paul Chambers' bass, almost tentative in the original, rumble forth in the Mastersound reissue. System noise, though perceptible in the original, assumes an aggressive and distinctly electronic character in the later version. To minimize the "new" noise, there is a fade-in at the head of the track that is absent from the original. Measurements in Fig. 8 confirm the subjective impression of both level change and increased nurse. At 4 khz the noise on the new mix is about 11 dB higher. Examining the recorded levels of the two CDs reveals that the maximum level of the Mastersound is (at this point in the recording) about 5 dB above the level of the original. This implies a net 6-dB increase in 4-kHz noise.

Note also that, whereas the noise spectrum of the original mix slopes downward, the remix noise actually rises slightly at high frequencies. At 10 kHz the noise energy is 17.3 dB above the original's, and at 20 kHz noise on the "new" Miles is 20.3 dB higher than on the old. With respect to the -96 dB Gaussian noise curve, noise on the "old" Miles is up 10.4 dB at 4 kHz and 6.9 dB at 10 kHz. The equivalent values for the new are +21.7 and +24.2 dB, respectively.
Based on the maximum recorded levels of the two releases, it might be suggested that one could reduce the intrusiveness of the noise on the Mastersound CD simply by turning down the volume 5 to 6 dB. That would be true if the level difference were stable, but it isn't. Figure 9 shows the maxi mum level difference in each minute of the two "So What" mixes. A maximum level difference of 6 dB (a doubling) in the first minute shrinks to 2.4 dB in the second minute, rises slightly, and then falls to about 0.5 dB in minutes 6 and 7 before rising again in the final two minutes. In remastering the recording, the overall dynamics of the performance were substantially altered from the original.
These changes have nothing to do with Super Bit Mapping. The greatly increased treble energy implies the use of equalization. If you take into account the level difference, it appears that perhaps 12 dB of lift was dialed in at 10 kHz, and possibly as much as 15 dB at 20 kHz. One effect of the EQ is to make much more prominent the cymbal work of Jimmy Cobb, often adding a "click" to cymbal attacks, the horn tones of Coltrane, Adderly, and, most prominently, Davis himself are also altered. While the saxophones have a slightly "breathy" timbre on the new version, Davis's trumpet tone seems greatly changed. The color spectrograms of Fig. 10 make this point more clearly than words. A spectrogram reveals the amplitude and frequency variation of a signal over time. Figures 10A and 10B show one ride-cymbal strike as the first vertical event on the left.
Note the greatly increased energy in the new cymbal (10B) versus the old (10A) and the way cymbal energy washes across the entire frame with much more of the orange color. Observe the well-formed partials (overtones) above 7 kHz in the old version and their absence in the new. The obliteration of the partials accounts for some of the difference in the sound of the trumpet, which is the second event. Close inspection reveals that the trumpet partials are much darker in the region from 1 to 2 kHz on the new than on the old. This is a further alteration of the trumpet timbre, and there is also a small, hard-to-see bass boost. The subjective result of the spectral differences is marked alteration in Davis's trumpet tone. The definitively "cool" Miles Davis sounds, momentarily at least, more like the brash Lee Morgan.
Figure 10C makes the equalization employed more obvious, with more conventional plots of amplitude versus frequency (the energy over the measurement period is integrated rather than broken out separately, as in the spectrograms). The use of a marked treble boost and some bass boost, though employed to varying degrees, was a characteristic of all three Mastersound re leases I examined. The technique is particularly apparent on another rerelease of a jazz classic, Dave Brubeck's Time Out (Columbia CK-52860).
Although noise is much less intrusive on Time Out, the results of the equalization used are similar. Paul Desmond's alto saxophone tone is even wispier than in the original version (CK-40585), and Joe Morello's drumming has a new, spectrally induced prominence.
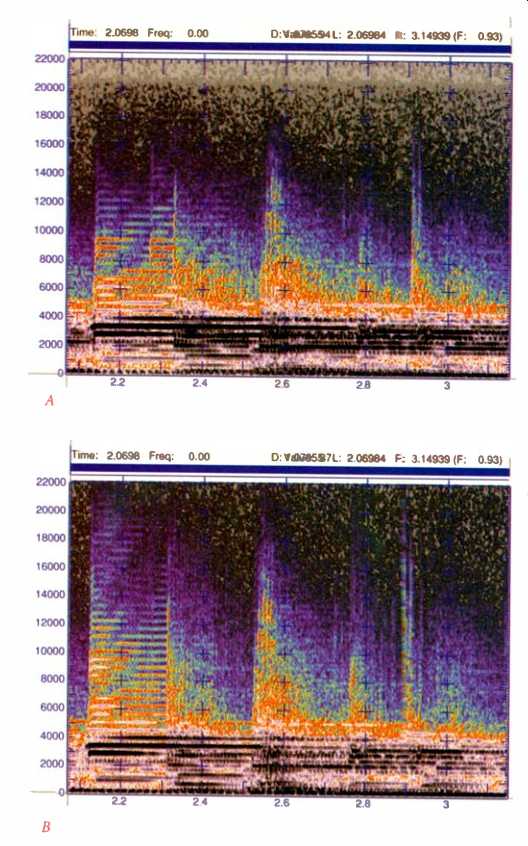
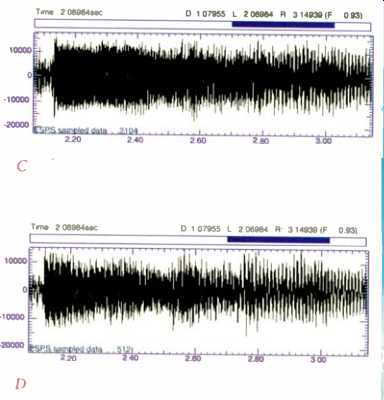
Fig.
12 Spectrograms of a guitar lick in "Leopardskin Pillbox Hat" on
the original (A) and Mastersound (B) CD releases of Bob Dylan's Blonde on Blonde.
The most prominent differences appear to result from reduced signal compression
on the new disc. Note the amplitude-versus-time plots in C and D and the much
greater peak-to-average ratio in the new (D) versus the old (C). Color key
(E) is for Figs. 12A and 12B.
And once again, there is technically induced alteration of musical meaning. The introduction to "Strange Meadow Lark" contains a high-treble piano arpeggio, shown as a spectrogram in Figs. 11A and 11 B (old and new). The reduced contrast between musical events in the new release is a result of the equalization used. While the overall maximum level in this segment is just a little more than 3 dB higher in the new Mastersound mix, the energy at 10 kHz is up 12 dB, and at 15 kHz it is up 17 dB. As in the case of "So What," the absence distinct band at the top of the new mix's spectrogram, above 20 kHz, indicates band width that now extends fully to 22 kHz.
Individual spikes show the hammer transients on the piano. Observe that they are much more intense (wider) in the new mix than in the original and contain more energy. The subjective effect of this is startling: The piano tone takes on a woody quality, more like a marimba. Further, Brubeck's phrasing is altered. The last note is now accented, whereas in the original mix it had a tentative, gentle quality. The amplitude difference, old to new, is +6.5 dB, or more than double for the last and highest note of the arpeggio compared to +3.2 dB for the entire musical figure. You can see the effect quite dramatically in the amplitude versus-time reductions of the spectrograms, Figs. 11C and 11D (old and new).

Musical consequences are also evident in the Mastersound rerelease of Bob Dylan's Blonde on Blonde (Columbia CK53016). The spectra in Figs. 12A and 12B show an effect that results primarily from the removal of processing found in the original (CGK-00841). The spectrograms show a guitar lick from "Leopardskin Pillbox Hat." In the original (12A), note how the black spectral lines in the low-kilohertz range blur together to create a relatively continuous sound of a "smoking" rock guitar. On the Mastersound CD, the individual attacks are more apparent, both in the spectrogram and to the ear. The difference is even more obvious in the energy-versus-time plots of Figs. 12C (old) and 12D (new). The probable cause is that compression applied to the original guitar track was either reduced or entirely removed in the remix. Although the musical effect is not easily described, it might be called "impaired groove." In creased treble lift on this track also emphasizes the individual guitar attacks-to its detriment, as the guitar riff is less than masterfully executed.
Through aggressive remixing and equalization, plus other techniques, the Mastersound tracks examined appear to have as their primary objective what might be called an "aesthetic update." The now dated balances of old recordings are revised to the extent possible, often with massive equalization. The process brings to mind the colorization of black-and-white movies. New audiences are recruited, and even those familiar with the originals may discover details they missed in the old versions when examining the new. That the old and new are markedly different is clear, but the audible differences are completely unrelated to the underlying technology of 20-bit recording and noise shaping. On the CDs examined, the noise from the original recordings entirely swamped the SBM process and rendered its use technically undetectable.
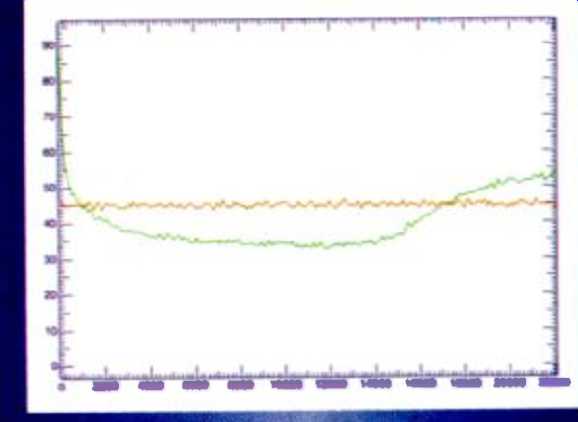
Fig. 13--Noise floor of an SBM-processed Sony Classical release of Emanuel Ax
playing Liszt's Piano Sonata in B Minor (green curve) compared with Gaussian
noise synthesized at -96 dB FS for reference (red curve.). This is one of the
very few CDs on which any benefit of noise shaping is apparent in the reproduced
noise floor.
Lest there be any misimpression that Super Bit Mapping itself does not work, Fig. 13 should banish it. Shown is the noise floor from a Sony Classical release of Emanuel Ax playing Liszt's Piano Sonata in B Minor (SK 48484). By 1 kHz the noise plunges beneath the -96 dB reference curve, there to remain until the SBM shaper pushes it back over at about 17 kHz. From 3 to 5 kHz the SBM curve is 7 to 9 dB below the reference. Allowing for the fact that the peak level on this recording is 4 dB below full scale and for the 2 dB needed to move from -96 to -98 dB, the theoretical 16-bit noise floor, we can conclude that the Ax recording does, in fact, exceed theoretical 16-bit performance by roughly 1 to 3 dB from 3 to 5 kHz and by a wider margin, about 5 dB, at higher frequencies up to 10 kHz. That is remarkable noise performance for a recording of a live instrument, in that it approaches 17-bit equivalence in the high-frequency portions of the spectrum.
While superbly quiet-no other recording examined achieved such low noise, al though a Dorian release, Memories of Bohemia by Anton Kubalek (DOR 90185), came close-the Liszt/Ax disc has a rather intimate perspective. Sounds of the artist's breathing and sundry mechanical noises from the instrument can intrude at times and detract from the brooding Lisztian majesty that might otherwise prevail.
What It All Means
In the end, we learn that noise performance approaching the 16-bit theoretical level is rare on real-world recordings, even with noise shaping and a 20-bit recording medium. The use of multitrack recording or complex recording consoles and multiple microphones probably precludes dynamic range in excess of 15 bits (and that's being generous). This is not difficult to understand: In mixing down from 16 channels, for example, the simple addition of the uncorrelated noise sources has the potential to degrade performance by 12 dB. Conventional consoles contain amplifiers by the hundreds, each contributing noise. In most productions a signal passes through a con sole twice, once when it is recorded and again when it is mixed down. If very low noise is somehow deemed mandatory to listening pleasure, then the most likely place to find it (there are still no guarantees) is on recordings made with minimum equipment: two mikes, two preamplifiers, a state-of-the art A/D converter and digital recorder, and no more.
All this assumes that the noise level of the listener's system and its environment con tribute less noise than the recording itself and that the system's dynamic range is sufficient to enable playback levels great enough to take advantage of the noise performance. In a technical paper, Sony suggests that a CD player with a signal to-noise ratio of 114 dB is needed to extract the full benefit of SBM. Of the 171 outboard D/A converters listed in the 1995 Audio Annual Equipment Directory, only 10 models (about 6%) meet or beat this specification. And that may not tell the entire story, since most D/A converters mute during a conventional S/N test, so the measurement winds up being only of the noise from the analog output electronics.
Should recordings that materially exceed 16-bit performance ever appear in substantial numbers, upgrades of many systems will be required to give listeners any shot at hearing the improvement--and those upgrades will extend beyond the CD player, for many line-stage preamplifiers and power amplifiers have noise floors well above the implied requirement.
The essence is this: To date, very few recordings actually meet, much less exceed, a 16-bit theoretical noise level. If they did, it is likely that the full difference could not be heard on most systems. The existing noise shapers, though they perform largely as expected alone, are often defeated in practice by the devices and signals in the recording or mastering systems that feed them. Simply put, recording studios and listening rooms are still too noisy, both acoustically and electrically.
Although noise shapers have little or no effect on the perceived noise of most real recordings, they do have sonic influences that can be heard. I have explored these effects by passing the same 20-bit master recording of a Steinway grand through selected noise shapers and evaluating the result. That exploration, a look at Apogee Sound's entirely different approach to 20-to-16-bit conversion, and the results of the first independent comparison of Pacific Microsonics' HDCD process to conventional recordings will be reported next. Expect surprises.
(adapted from Audio, Mar. 1996)
Also see:
Digital Deliverance (Noise shaping, HDCD, etc.) (Apr. 1996)
Link | --The Trouble with Jitter (Jan. 1996)
= = = =