by Martin Clifford
THIS IS THE FIRST of a series of articles intended to act as your guide to high-fidelity sound. Their purpose is not to make you a technician or engineer, but to supply an understanding of the electronic principles on which high fidelity is based.
Buying high-fidelity equipment presupposes a certain measure of user sophistication, but the ability to talk about dB, IM, THD, bandwidth, signal-to-noise ratio, or anti-skating, doesn't necessarily involve understanding. Words such as these, and similar words and phrases, formerly confined to engineering discussions, have become part of the daily language of high fidelity. It is the intent of this series to strip these words of their mystery and, at the same time, to supply an overall concept of the roadblocks that stand between the creation of a sound source and the listener. Math will be detoured unless completely unavoidable. The design here is for comprehension, not engineering proficiency.
THERE ARE MANY DEFINITIONS of high fidelity for the simple reason that there is no single, satisfactory, all encompassing concept. The manufacturer of a bargain basement FM receiver refers to his product as high fidelity; so does the manufacturer of a thoroughly researched component selling for ten times the price. Two different units and two different definitions of high fidelity.
The search for high fidelity is like the search for the Holy Grail; elusive, tantalizing, always out of reach. And therein lies the charm and beauty of high-fidelity sound. It's a standard beyond obtaining. But each new technological advance, each new bit of research brings us that much closer. In the meantime we have in our homes music of a quality which was undreamed of just a few short decades ago.
But what is so difficult about high fidelity? Surely it should be easy to record an orchestra, or the human voice, convert it to its electrical equivalent, and then to reproduce it. Yes, that's no problem, for it has long since been solved. What is now involved is the reproduction of more subtle factors. If an orchestra records in a music hall, what we now want is to reproduce not only the orchestra, but the peculiar and individual acoustics of the music hall, for these acoustics have a direct effect on the recording. The room in which you listen, though, has its own acoustics. It is probably smaller; its reflective surfaces more or less sound absorbent. And, during a recording, not only is the direct sound recorded, but also the ambient sound-the sound reflected from walls, ceilings, people, seats. But when you play disc or tape, or listen to a receiver, your own room doesn't disappear. It adds its own ambience, and so what you hear isn't a true reproduction. Yes, headsets might solve this particular problem, and in this sense headsets are remarkably closer to true sound reproduction than speakers. Headsets, though, may present a psychological disadvantage. When you attend a live concert you have nothing pressing against and enclosing your ears, and so, to some people, headsets may prove a mental stumbling block.
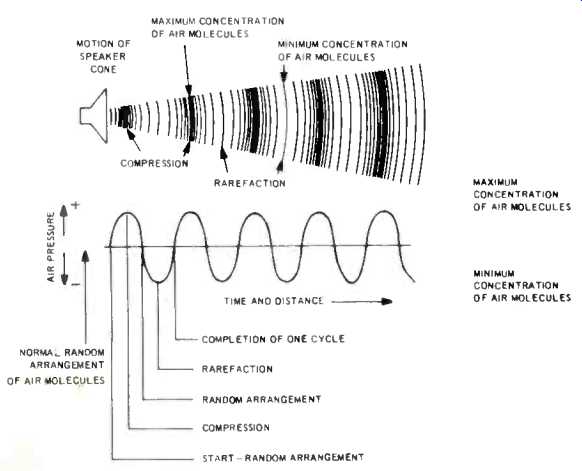
Fig. 1--The wave is a graphic representation of the compress the action
of air molecules.
Sound Waves
Modern high-fidelity reproduction systems consist of arrangements of highly complex electronic circuits, far more sophisticated and detailed than they were a few years ago. But while high-fidelity circuitry has made tremendous forward advances, the basic stuff and substance of high fidelity has always remained the same. We start with sound.
Sound is rather unique for it is a form of energy, and there aren't too many such forms. Electrical energy is another one. So are light, heat, mechanical, and nuclear energy. And when you include chemical energy you have just about completed the list. This is a small compilation supplied by a nature generally profligate in its varieties. Fortunately it is enough. Equally fortunately, we can convert one form of energy into another, desirable since it leads directly to high-fidelity music reproduction in the home. We can take sound energy, change it to electrical energy, and then get it back to sound energy again. That is exactly what we do when we broadcast signals and receive them.
How Sound Waves Are Produced
It's easy to produce sound waves, too easy in fact, for it is almost impossible not to do so. We are constantly surrounded by sound and cannot avoid it. Listen, and you will hear the sound of your own breathing. You can escape from it but the alternative is unpleasant. Since it would be intolerable to be consciously aware of sound at all times, our brains perform a protective function and shut out most of it. We do need this help, but when we listen to music we must really learn to hear all over again. Listening to music requires a conscious, intelligent effort. It not only takes effort, it demands continuous practice.
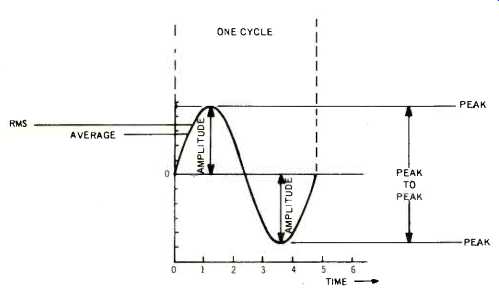
Fig. 2--A cycle is one complete waveform. The units along the bottom line
are usually in seconds. The four ways of measuring this wave are average, rms
(also known as effective value), peak, and peak-to-peak. These terms are often
used in manufacturers' specification and catalog sheets.
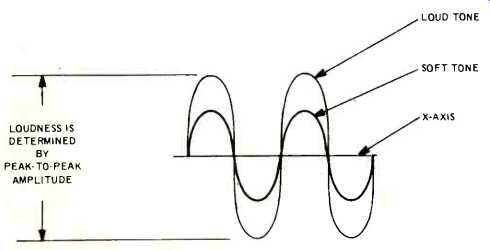
Fig. 3--The horizontal line or x-axis represents a condition of no sound or
random arrangement of air molecules. As peaks become smaller, the waveform
approaches the axis caused by a reduction in the compression and ... the air
molecules.
The Production of Sound
We live at the bottom of an ocean of air, a fortunate circumstance since it enables us to hear as well as breathe. Although invisible, air is made of particles of matter we call molecules, just as a brick wall is made of particles of matter. The difference between the two is in the kind of molecules used, their density (that is, the number of molecules per cubic inch), and their freedom of movement. Again, we are fortunate that air molecules can move for it is their motion that helps produce sound. However, this statement must be modified somewhat for air molecules are apparently in constant motion. Any wind is evidence of that.
But we aren't interested in the random motion of air molecules, but in their movement that results in sound. We can get sound if we force air molecules to travel in large groups, much like a pack train. This compacting of molecules, forcing molecules to acquire a greater unit density, is called compression. But if we compress molecules into a smaller space, we must take them from somewhere. Sound doesn't create molecules; it simply uses those that are available. Consequently, some parts of the space that surrounds us are deprived of molecules, an action known as rarefaction. Sound, then, is related to the compression and rarefaction of air molecules (Fig. 1).
This compression and rarefaction of air molecules is what happens when a musician draws a bow across a string. The vibrating string causes the air molecules to rearrange themselves in a very particular way, quite different, for example, from that resulting from a vibrating skin of a drum. In your home, the moving cone of your speaker produces compression and rarefaction of air molecules in an identical manner, enabling you to distinguish between a violin and a drum. If a speaker cone is able to do this reasonably well, we call it a high-fidelity unit. To the extent to which the cone adds its own compressions and rarefactions of air molecules it is not high fidelity, for then you are not longer listening to violin or drum music, but to cone music.
Kinds of Sound Waves
It is quite unlikely that anyone else in the world writes in quite the same way you do, a simple fact on which banks place great reliance. Similarly, no two sound producing devices yield exactly the same combination of air molecules. The particular rearrangement of air molecules from all those that are present at random is the signature of the device producing the sound. The sound can be stronger or weaker, just as you can write your name larger or smaller, but there does seem to be an almost infinite number of ways in which air molecules can be patterned. This gives us the large variety of sounds which most of us take for granted. And, instead of referring to them as compressions and rarefactions of air molecules, an awkward phrase at best, we simplify and call them waves.
The Sine Wave
Although there is substantial evidence to the contrary, man does try to be a rational creature, particularly when it concerns science or some branch of it, such as electronics. There are tremendous numbers of waves, of all sizes, shapes and descriptions. Offhand, it would seem a chaotic condition and while we cannot, indeed would not, want the number of sound waves reduced, we can make some attempt at grouping them.
The simplest of all these, the most basic of all sound waves is called the sine wave. Technically, it is the graph of a trigonometric function called the sine. Not so technically, it is a readily reproducible acoustic ruler against which we can measure or compare other sound waves. It is rather easy to produce sine waves by electronic means. Devices that do this are called signal generators, or more simply, generators. But it isn't quite that easy to produce sine waves directly from musical instruments, for they ordinarily yield more complex waveforms.
The sine wave is not only our standard, but can be measured in a number of ways, leading to a set of values which, in turn, can be used as standards against which other kinds of waves can be measured or evaluated.
The maximum strength or amplitude of a waveform, sine or not, is called its peak value (Fig. 2). Ordinarily, a horizontal line is drawn through the exact center of the sine wave, dividing it into two equal portions, an upper and a lower. The upper part is called the positive half, and the lower the negative, although these terms are arbitrary and are used to identify the two halves. The horizontal line is synonymously termed the X axis, a reference that has about as much reality as the circumferential line drawn around the earth and known as the equator. It is just a convenient and useful fiction.
The distance from the x-axis to the maximum portion, either positive or negative of the wave, is called the peak value or peak amplitude, words you may often come across when reading manufacturer's spec sheets. Using the same identifying process mentioned earlier, the upper is the positive peak; the lower the negative peak. The distance from the positive to the negative peak is the peak-to-peak value, often abbreviated as p-p. Amplitude could also be called the loudness of sound and is determined by the difference between the maximum compression and maximum rarefaction (Fig. 3).
Instantaneous Values
The formation of a complete sine wave takes time. The two peak values, positive and negative, represent just two moments or two instants in the passage of time required for the completion of a sine wave. But we can have other instants as well. We can stop the conditions producing the wave at any moment we wish, and measure the amplitude at that moment. The height of the wave above the x-axis of that instant is known, logically, as the instantaneous value. A wave can have any number of instantaneous values, beginning with zero at the start of the wave and reaching maximum at its peak (Fig. 4).
Average And RMS Values
Since the sine wave is to be the electronic ruler against which we will compare other waves, identifying the positive and negative peak values only makes about as much sense as calibrating a yardstick solely in half inches, a self-defeating gesture. To have an additional reference, we sometimes use average values.
To find the average value, we select an arbitrary number of instantaneous values using either the positive or negative half of the wave. We may select 50 or 100 instants during which we will "freeze" time and make a measurement from the x-axis to the waveform. Adding these values, and then dividing by the total number of instants, supplies us the average value. This turns out to be approximately 63% of either the positive or negative peak values.
Another measurement, more commonly used than average value, is root-mean-square value, abbreviated as rms, also found on manufacturers' spec sheets.
The rms value of a sine wave is obtained in much the same way as the average value, but there is a slight variation. Instead of adding each instantaneous value directly, these values are squared. The squared values are then added and the square root is taken of the sum. The rms value of any sine wave turns out to be approximately 70.7% of the peak value.
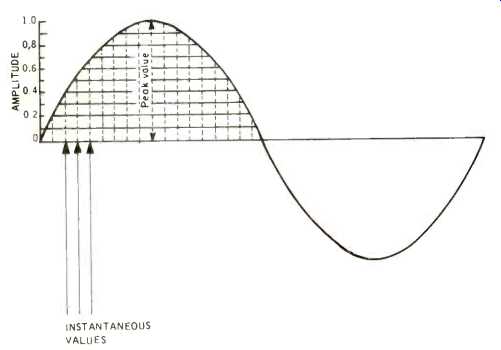
Fig. 4--A wave can have any number of instantaneous values, shown here by vertical
lines drawn from the x-axis to the waveform. Peak value is an instantaneous
value. Each sine wave has two such peaks; a positive peak and a negative peak,
representing maximum compression and maximum rarefaction of air molecules.
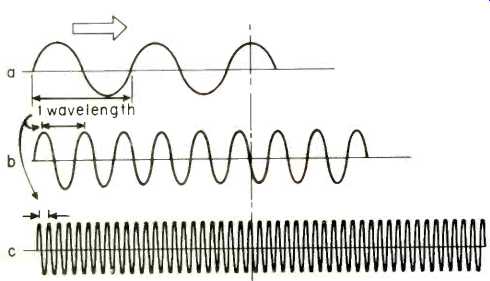
Fig. 5--Wavelength is the distance from start to finish of a single wave,
or from the positive peak of one wave to the peak of the adjacent wave. Frequency
is the number waves per second. The frequency is increasing, a, to b, to c.
Meaning Of Frequency
The number of sine waves available per unit of time, the second, is known as frequency. If you have just a single, complete sine wave consisting of a positive half and a negative half, and if this wave requires one second from start to finish, then the frequency is one complete sine wave per second. Since a single complete wave is more conveniently known as cycle, this particular frequency is one cycle per second, abbreviated as cps. The cycle per second has given way to the Hertz, to honor Heinrich Hertz, noted scientist of the late 19th century who pioneered in wave transmission. The Hertz, abbreviated as Hz, is equivalent to the cycle-per-second. Thus, 100 Hz is the same as 100 complete waves, all of which are accomplished in just one second.
Naturally, if we are going to have 100 waves in the same time it takes to complete 1 wave, the 100 waves are going to be squeezed. The distance from the start of a single wave to its completion is known as its wavelength, and is usually measured in meters. As we get more waves per second, the individual waves huddle closer together, and so the distance from start to finish of each single, complete wave becomes less. More elegantly stated, as frequency (number of waves per second) increases, wavelength (distance of wave from start to end) decreases. While both types of measurement are used, you will find frequency units indicated directly on the dial of your FM receiver. These numbers may begin with 86 and end with 108, and indicate millions of Hz. Thus, 86 is 86 megaHertz, an easier way of writing 86,000,000 Hz. Less chance of losing a zero or two (Fig. 5).
Frequency Response
Although we cannot see them without some electronic assistance, waves do take up space, and so if we are to have waves travel without interference through the air or electronic circuits, we must provide a roadway for them, just as we need four or eight lane highways for autos, depending on traffic conditions. The ability--or the inability--of a circuit to pass a large group of frequencies, is known as frequency response. Audio amplifiers, for example, are rated (among other ratings) on their ability to amplify uniformly a large band of frequencies ranging from as low as 15 Hz or 20 Hz to as much as 30,000 Hz or more.
Pure Tones
Because a sine wave is used as a wave reference, it is known as a pure tone. But this isn't the only reason for this designation. It is a pure tone because it isn't associated with other tones. It exists alone. Theoretically, it is possible to produce a pure tone on the violin if a string is bowed in its exact center. This is a most unusual condition since a musician, even when playing a single tone, vibrates his hand so as to produce anything but a pure tone. Further, as the violinist moves away from the exact center of the string, the string will not vibrate as a whole, but in parts. Finally, the string can vibrate as a whole and in parts, simultaneously, a condition which also applies to the piano. The result is that we hear, not a single pure tone (from which we get the word monotonous) but rather the pure tone plus a number of overtones. It is the sum of pure tone plus overtones which lends beauty to music. It is the number of overtones, their amplitude, the way they start and finish, that determines the timbre of a tone, the particular characteristics of a tone that enable us to distinguish between a violin and a flute. If you want to hear pure tones, listen to the low notes of a flute or the sine-wave output of a generator.
The combination of a basic sine wave plus overtones produces a complex wave. Each overtone is actually a sine wave also, but when combined with a fundamental the sum of the waves is anything but a sine wave.
The fundamental sine wave of a musical tone has a particular frequency. For bass tones, the frequency is low; for treble tones the frequency is much higher. Each overtone, though, is higher in frequency than the fundamental. The second overtone has twice the frequency of the fundamental, the third three times the frequency, and so on. But if we combine a fundamental and a number of overtones, we no longer contend with a single frequency, but a group of them. And that is what you hear when listening. Again, whether, you will hear the fundamental plus all the overtones depends on the equipment you have. Loss of some of the higher frequency overtones is called distortion, but this distortion is just one of the many ways in which you can be robbed of your musical enjoyment.
Transducers
Sound waves, such as those produced by musical instruments or the human voice, can be changed into electrical form by a microphone, a device belonging to a general class of instruments known as transducers. A transducer changes one form of energy to another. Microphones change sound energy to electrical energy. A speaker is a transducer, even though its work is the antithesis of a microphone. Speakers change electrical energy into sound waves. The concepts of wavelength, frequency, and measurements such as average, rms, peak and p-p, are more commonly applied to electrical, rather than sound waves.
The word "harmonic" is used in place of overtone after a sound wave has been converted to its electrical equivalent. Harmonics and overtones are the same; it all depends on when you use them.
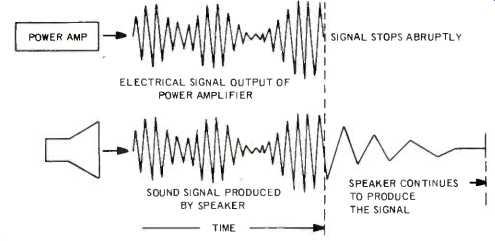
Fig. 6--The inertia of the cone makes it difficult for the cone instantaneously.
The movement of the cone after the of the signal produces sound not present
in the source.
Transients
Although music consists of fundamentals sine waves plus related overtones yielding a complex waveform, we think of the music as being continuous. The pitch and amplitude may change, but we still consider it an uninterrupted sequence of sound. Actually, though, music contains sounds, known as transients, which start abruptly and which may also terminate that way. Bowing a violin string can produce a sound whose instantaneous amplitude is very large. Percussion instruments are more dramatic examples. And so, electronic circuits, such as amplifiers, must not only be capable of handling a wide range of frequencies, but transient sounds as well.
An inability to do so results in transient distortion, a condition in which an electronic circuit modifies the transient to conform to its own limitations. Transient tones can cause amplifiers to act as generators, producing signals of their own. And so, an amplifier with poor transient response becomes a member of the orchestra, adding sounds not present in the original. Because the amplifier now has two signals to work with the original transient and the self-produced signal-it can become overloaded. Incapable of handling so much signal, the amplifier distorts, a condition we could call overload distortion.
A transient can stop as suddenly as it starts. Since a speaker cone has inertia, it may continue its movement, thereby producing sound when no sound should exist. And so transient distortion can exist right at the last moment, at the speaker output (Fig. 6). There are many kinds of distortion, other than transient, and the extent to which a sound reproducing system can avoid them is an indication of its right to claim the label "high fidelity."
Frequency Distortion
Sounds produced by the human voice and musical instruments range from a low of around 16 Hz, or possibly a little lower, to around 18,000 Hz, or somewhat higher. The piano has a range of about 26 cycles to 4,096 cycles, with almost all musical instruments coming within this spectrum. And, since the end keys of the piano are rarely used, the range is really narrower than indicated. The piccolo is an exception and can get up beyond the high notes of the piano, but the organ is really the tonal master. It extends from a low 16 cycles to 16,384 cycles.
What we are talking about here are fundamental tones. But each of these tones is accompanied by overtones, some of which are 20 times the frequency of the fundamental. And so, if we're talking about a fundamental of 3,000 cycles, the 20th harmonic would be 20 x 3,000 = 60,000, well outside human hearing range, regardless of age, sex or musical training.
The third overtone of a 5,000 cycle tone gets very close to the auditory limit for most people.
While we may refer to 16 Hz to 18,000 Hz as the audible range, it doesn't follow that this is your range. What you can hear depends on your state of health, the condition of your hearing apparatus, your sex, your age, and quite possibly your brain or mental attitudes. Further, you have no assurance that you hear equally well with both ears. However, high-fidelity equipment is designed with the assumption that your auditory response is perfect.
However, sound reproducing systems, like human beings, are also not perfect. If a music system is incapable of responding to and amplifying equally well all of the sounds-the wide gamut from low to high frequencies-it is guilty of frequency distortion. Oddly enough, both amplifiers and human hearing are capable of improvements-the electronic system through better design and the human through more careful listening, musical education and experience. If your hi fi doesn't sound as good today as it did originally, then it's possible you have improved, assuming no deterioration in your gear.
Frequency distortion doesn't start at any particular place. It may begin with the first transducer, the microphone, or the pickup unit of your record player, or your speakers. Frequency distortion often consists of a roll off at the low and high ends of the sound range. Less often, it consists of higher or lower than normal amplification in the midrange.
Harmonic Distortion
A pure sine wave contains no harmonics and is a single frequency waveform. Its strength can be varied but this does not change (or should not) its frequency. A harmonic can be an odd or even multiple of the fundamental. If the fundamental is 440 Hz, the second harmonic is twice this or 880 Hz.
Since the second harmonic has a frequency twice that of the fundamental sine wave, it is one octave removed from it.
A fourth harmonic would be 4 x 440 = 1,760 Hz. Both the second and fourth harmonics are also known as even-order harmonics. The third harmonic is 3 x 440 = 1,320 Hz and the fifth is 5 x 440 Hz = 2,200 Hz.
A fundamental plus a single harmonic, the second, combines to form a complex wave (Fig. 7). The appearance of this wave depends directly on the time of starting and stopping of the two waves, and their strengths relative to each other. Just a simple shift in amplitude or the time at which they both reach zero can result in a tremendous number of different complex waves. The problem is further complicated when higher-order harmonics are involved. Harmonic distortion involves the changing of the time or amplitude relationships of harmonics to the fundamental.
Harmonic distortion takes place when additional frequencies are produced--frequencies which are multiples of the fundamental. If a fundamental wave having a frequency of 440 Hz becomes distorted, the distorted wave can be resolved back into a fundamental, but not a fundamental alone. It will be a fundamental plus one or more harmonics, all of which are sine waves. Whether these harmonics will be annoying will depend on their amplitude and frequency. Harmonic distortion may cause reproduced music to sound artificial. Total harmonic distortion, THD, is the sum of all the harmonics produced by a distorting element. Harmonic distortion can be evaluated by feeding a pure sine wave into an audio system, measuring the amplitude of harmonics produced with relation to the amplitude of the fundamental, and expressing this as a percentage. Thus, 1% harmonic distortion means that the amplitude of the harmonic is 1/100 of the original pure sine wave input.
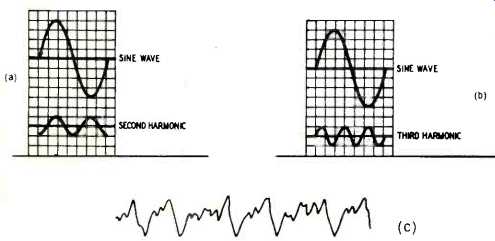
Fig. 7--Complex waves consist of fundamentals plus related harmonics. The
combination of these waves results in a complex waveform that has very little
resemblance to a sine wave, (a) sine wave and its second harmonic; (b) sine
wave third harmonic; (c) complex waveform of a violin tone … can be resolved
into a sine wave plus a number of sine waves.
Intermodulation Distortion
Intermodulation distortion, or IM, another type of distortion, takes place when two or more waveforms travel through an electronic device at the same time, and this is usually the case. Assume a wave of 440 Hz and 1,000 Hz are being amplified simultaneously, and that the lower frequency is quite strong, so much so that it causes the amplifier to act in a nonlinear manner-that is, it will not amplify without distorting. The 440 Hz wave has its greatest strength during the times of its positive and negative peaks, and so it may be only during these intervals that the amplifier distorts. But the higher frequency wave--the 1,000 Hz wave--will have a number of positive and negative peaks during the time of distortion and so this will become distorted.
The result will be a variation of the 1,000 Hz wave at a 440 Hz rate. The term intermodulation distortion refers to the fact that one wave modulates or changes the waveform of another.
But whenever a waveform is made to change its shape, new harmonics are produced. And since these harmonics are not supposed to be present, they are called distortion products.
IM distortion is evaluated by a testing device designed to receive two signal inputs, a low- and a higher-frequency signal.
At the output, the amount of low-frequency signal contained in the high-frequency signal is measured and expressed as a percentage. Thus, 2% IM distortion means that 2% of the low frequency signal has become part of the higher-frequency wave. IM distortion is considered much more serious than harmonic distortion since its effects are more noticeable and annoying.
Phase Distortion
Waves do not always start and stop at the same time, any more than you would expect all the trains in a depot to pull out simultaneously. The time separation between pairs of waves is called phase. If two waves begin at exactly the same time, and they rise and fall in step, they are in phase; if not, they are out of phase.
Waves do not travel through electronic equipment with the same speed. Electronic parts may favor the passage of some frequencies while temporarily barring others. As a result, waves of different frequencies which may enter electronic equipment simultaneously, or which may be only slightly separated in time, may have their phase differences increased.
This change in time separation is called phase distortion, but it is ordinarily not noticeable. Phase distortion isn't one of the terms you will usually find in manufacturers' specs. Phase becomes important in connecting speakers or may become noticeable in speaker systems.
Voltage
When a transducer such as a microphone, changes sound energy, the result is a corresponding wave, but in electrical form. The wave is actually a voltage with the sine wave sometimes referred to as a voltage sine wave. Another name for voltage is electromotive force or emf. While the basic unit is the volt, we are often concerned with much smaller amounts such as the millivolt, or thousandth of a volt, and microvolt, or millionth of a volt. The signal picked up by an FM antenna is in the order of microvolts. It would take an amplification of one million to increase the microvolt to a volt, something easily done by modern equipment.
What's Next
We started with something quite simple-the sine wave, but soon made matters complicated, for we don't listen to sine waves, but to complex waves-combinations of sine waves and harmonics. We've already indicated some of the dangers that await the complex wave in its travels through electronic components, but that is just the beginning of the story. We must somehow manage to get the sound to your home, either by broadcasting it or by recording it on disc or tape. All during these operations the wave is in constant danger of change.
Part of the problem stems from the fact that no wave is an island unto itself. It must coexist with other waves, joining with them, but not altering them, nor permitting itself to be altered. The whole concept is known as high fidelity.
The next step is to consider electronic parts--the parts we use to hold our waves, amplify them, and deliver them in augmented form, but not distorted. And that's coming next!
( Audio magazine, May 1972)
Also see:
The Language of High Fidelity--Part III: Basic Electronic Components (cont.) (Aug. 1972)
The Language of High Fidelity--Part VII: The Basic High-Fidelity System (Dec. 1972)
The Language of High Fidelity--Part VIII (Feb. 1973)
Language of High Fidelity--Part XI (May 1974)
= = = =