The Function Generator (Nov. 1970)

Home | Audio Magazine | Stereo Review magazine | Good Sound | Troubleshooting

by NORMAN H. CROWHURST

THE FUNCTION GENERATOR is a fundamentally different oscillator from its predecessors. The nearest to it was the multivibrator. The old sine wave oscillator worked, essentially, by using a tuned circuit or other frequency-selective network and applying gain to make it oscillate at the required frequency.

Oscillators that used a phase-shift or bridge-type feedback, or even the twin-T type, all employed the same principle. What the reactive components, of whatever combination and configuration, determined was frequency, basically of a sinusoidal signal. If it oscillated too hard, the shape departed from true sinusoid, but that was the shape with which it started, before it got big enough to distort.

And gain was the other adjustable quantity. When gain was just a whisker more than needed, the waveform built up until something stopped it. In a good oscillator, an automatic circuit would turn down the gain; in a poor one, distortion would reduce gain, because all the signal handled was not of the true frequency.

And if gain went a whisker too low, the oscillation would die away. However good a sine-wave oscillator, it has these sort of "bouncy" characteristics, of growing and dying. The function generator uses a totally different starting point. Instead of frequency and gain being the basic reference quantities, as in the sine wave generator, the function generator uses time and amplitude as the basically inter-related quantities.

Figure 1 shows one way of starting such a design. Transistors Q1 and Q2 alternately charge and discharge capacitor C, as one or other of them is triggered into and out of action. The rate of charge or discharge is set by the voltage applied to their bases. As shown, the emitters of Q1 and Q2 have a 1-K resistor each. This converts the voltage from base to supply point into a constant current of the same number of milliamps.

Transistors Q3 and Q4 serve to switch off the transistor Q1 or Q2 that is momentarily inoperative. Suppose Q1 is momentarily charging C more positively. For this to happen, Q6 short-circuits Q3, so that the only current in the 1-K resistor between the emitters of Q1 and Q3 and supply plus is due to Q1 emitter current.

To maintain Q6 in saturation, Q4 must also be conducting. The 1.5-K collector resistor, feeding the base of Q6, sets the collector and emitter voltage of Q6, which is saturated, at plus 12 volts, due to the drop in the 1-K resistor in the emitters of Q2 and Q4. This means the emitter of Q2 is more positive than its base and thus it is cut off. Only Q1 is supplying current that affects the voltage on C.

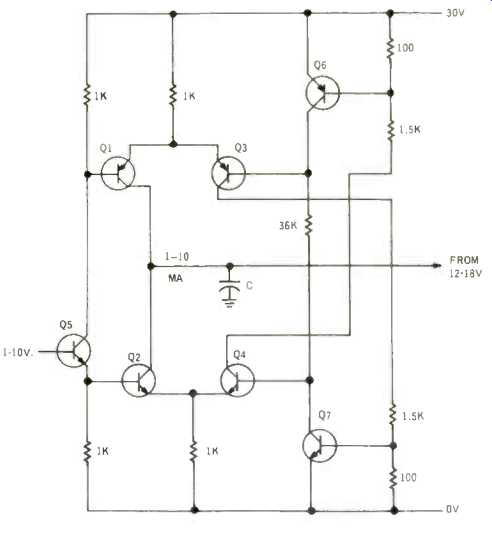
Fig. 1--The switching and charging, discharging part of a function generator.

When the current through Q1 has charged C to the point where its voltage should go the other way, a trigger circuit will reverse the cycle. Then Q3 will saturate, along with Q7, and Q4 and Q6 will be non-conducting.

When Q4 saturates Q6, Q4 in turn is saturated by the 36-K resistor between the bases of Q3 and Q4. Q7, being nonconducting, allows the current in this resistor to saturate Q4. Similarly, when Q7 saturates, Q4 is cut off, cutting off Q6, thus allowing the current in the 36-K resistor to saturate Q3 and maintain the other bistable condition.

In this circuit, the rate, or slope of both 'up' and ‘down' is controlled by the input voltage applied to Q5. As this has a 1-K resistor in both emitter and collector, the voltage is duplicated, relative to the respective supply points, at the bases of Q1 and Q2. By applying from 1 to 10 volts d.c. at the base of Q5, the charge and discharge rate may be varied from 1 to 10 milliamps.

If C is made 1 microfarad, 1 milliamp will charge or discharge it at the rate of 1 volt per millisecond. Making the height of the wave 6 volts ( from 12 to 18, as shown) means the 'up' slope will take 6 milliseconds and the `down' slope will take 6 milliseconds: a period of 12 milliseconds, or a frequency of 83.3 Hz.

Pushing the control voltage up to 10 volts, the charge and discharge rate will change to 10 milliamps, resulting in charge and discharge times of 0.6 milli-second, or a 1.2 millisecond period: frequency 833 Hz. Using different values of C enables other frequency ranges to be obtained. Using a capacitor of 0.1uF, the frequency range will be from 833 Hz to 8330 Hz, for the same control voltage range.

Figure 2 shows the next step toward the design, by adding a suitable trigger circuit. First step is to provide the trigger voltages, which is achieved by stringing a resistor chain across the supply. The trigger circuit consists of Q8, Q9, Q10, Q11. As the bases of Q10, Q11 are at 12 and 18 volts, with the polarity of transistors shown, all four transistors are normally non-conducting.

The only time they conduct is at the moment when the voltage at the bases of Q8 and Q9 goes either more positive than 18 volts or more negative than 12 volts.

When the voltage on C is moving positive, Q1 is conducting, Q4 and Q6 are saturated, and Q7 is non-conducting.

When the voltage causes Q8 to conduct, it triggers Q10 along with it, and this triggers Q7 into saturation, which short-circuits the base of Q4, cutting it off, and thus discontinuing the saturation of Q6. This allows Q3 to saturate, switching Q1 off, while Q4 being cut off allows Q2 to start conducting to reverse the charge direction.

Function Generator

When the voltage on C gets so that Q9 starts to conduct, Q11 triggers Q6 into saturation, cutting off Q3 and Q7 and allowing Q4 to saturate, again reversing the charge direction. This flipping will carry on with close precision.

This is a precise triangular waveform, with very linear sides, because the charging current is controlled entirely by the voltage on the bases of Q1 and Q2, in conjunction with the emitter resistor. For example, 5 volts across the 1-K emitter resistor sets the current at precisely 5 milliamps, and the collector current follows it. Precise choice of 1-K resistors, both in the emitter and collector of Q5 and in the bases of Q1, Q3 and Q2, Q4, is needed to effect an exactly symmetrical wave.

The next step will be to use this triangular wave as a basic form from which to generate other waveforms. A series of appropriately biased diodes and resistors can change the slope of the waveform at different points, until a very close approximation to sinusoidal is achieved.

The advantage of this method of making a sine wave is that it works down to a very low frequency. For example, by using a 1000-µF capacitor for C, the frequency range, with the same values otherwise, can go down to from one cycle every 12 seconds to one cycle every 1.2 seconds. It will trace these waveforms as precisely and as immediately as it does those of more conventional audio frequency.

A 1/12th Hz sinusoidal oscillator, using the older circuits would take minutes--perhaps half an hour--to settle to a stable amplitude, even if a good sine waveform was possible. This circuit starts to generate the perfect sine wave immediately.

But we do not have a sine wave yet. All we have is a triangular wave, with a peak-to-peak voltage of 6, using a 30-volt supply. To be able to adjust the sine waveform precisely, it will be advantageous to make the wave bigger first. And to set its limits as precisely as the 6-volt limits at 12 and 18 volts on this embryo wave.

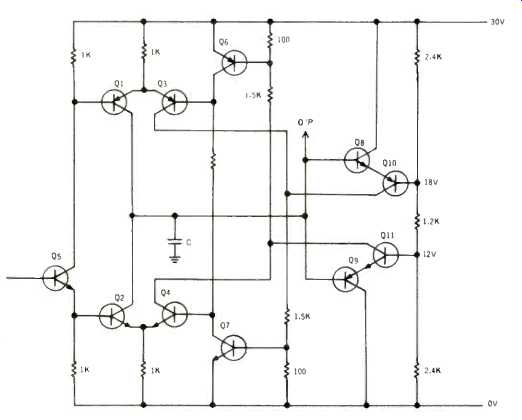
Fig. 2--The trigger elements added to the circuit of Fig. 1.

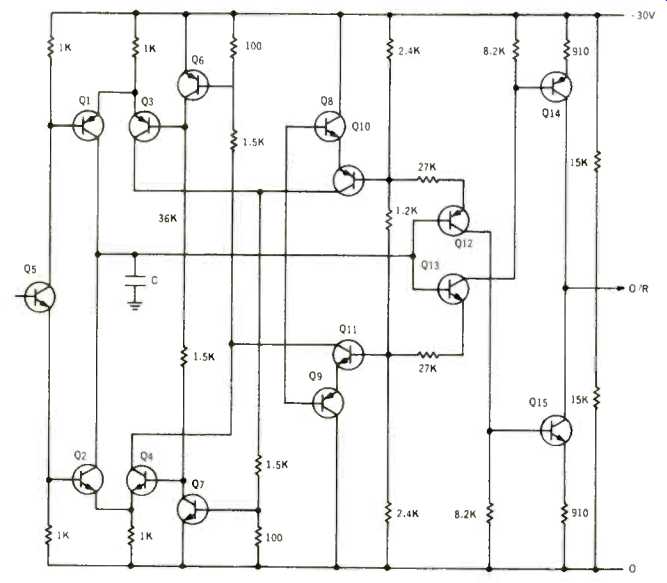
Fig. 3--The complete circuit, with amplification added, so the output can be almost as large, peak to peak, as the supply voltage. As the whole thing is direct coupled, the circuit can be used for very low, fractional frequencies.

Figure 3 shows the same circuit with 4 more transistors added that will achieve this. Q12 and Q13 take the triangular voltage, which is 6 volts peak to peak, and convert it to a triangular current waveform. The 27-K emitter resistors convert the 6 volts maximum voltage to 6/27= 222 microamps maximum current.

The 8.2-K collector resistors again convert these currents to voltages, except that there are now two of them, located adjacent to the supply voltages, on the d.c. scale. Before determining the voltage, consider the parallel effect of the transistor bases, Q14 and Q15, which have 910-ohm emitter resistors. Assuming a beta of 50, this refers back to the base as 45.5 K. In parallel with 8.2 K, this makes 7 K.

So the voltage at the bases of Q14 and Q15 is triangular, of 0.222 x 7 = 1.56 volts peak. When C is charged to its maximum positive, Q12 current falls to zero, as does Q15 current, to which it is coupled. At the same time Q13 current reaches 222 microamps and Q14 base reaches 1.56 volts negative of supply plus.

The emitter voltage of 1.56 volts maximum, on Q14 or Q15, across 910 ohms, results in a collector current of 1.56/910= 1.72 milliamps. The other current, at this moment, is zero.

The collector load for Q14 and Q15 is the two 15-K resistors across the supply. These provide a source voltage of half the supply, or 15 volts, and a load resistor value of 7.5 K. The maximum current of 1.72 milliamps in 7.5 K yields a voltage of almost 13 volts peak, each way, or 26 volts peak to peak.

Quite precise choice of values may be needed to effect this degree of precision.

Some adjustment may be needed to compensate for deviation from the theoretical beta value used, of 50, although this is not too critical in the mode of amplification used, where current gain is fairly swamped by a form of voltage feedback.

In the next article, we will take this circuit and modify it to yield a sine wave, also discussing the degree of accuracy to which the sine wave may be approached. In this presentation, we have described the effect of the values chosen, rather than showing how to calculate the values required.

The method of calculating works backwards most of the time. The values in the circuits of Q1 through Q11 are chosen to provide just over saturation, or the desired voltage change at Q3 or Q4 for switching when saturation occurs. The resistor string is designed to take 5 milli amps, which will not be affected by base current to Q10 or Q11, or by emitter current through the 27-K resistors, appreciably.

The values in the amplifier stages Q12 through Q15 were worked out backwards, using 15-K resistors, calculating the collector load, back to collector current, emitter resistors, base resistors, and so forth.

(adapted from Audio magazine, Nov. 1970)

Also see:

A Sound-Level Meter (Dec. 1970)

Negative Feedback by Norman H. Crowhurst (Apr. 1970)